Является ли проблема четырех красок такого рода математической теоремой? Если это так, то ее можно считать «истинной» только в том случае, если ее или какую-нибудь другую тесно связанную с ней теорему включить в качестве нового недоказуемого постулата в расширенную дедуктивную систему.

К сожалению, доказательство того, что пяти красок достаточно для раскраски карт на плоскости, а шести или более красок необходимо и достаточно для раскраски некоторых более сложных поверхностей, слишком длинно, чтобы приводить его здесь. Некоторое представление о том, как протекает доказательство этих теорем, читатель сможет получить из следующего остроумного доказательства теоремы о раскраске в два цвета.

Рассмотрим все возможные карты на плоскости, образованные прямыми. Примером такой карты может служить обычная шахматная доска. Менее правильный узор изображен на рис. 221 слева.

Достаточно ли двух красок для раскрашивания всех таких карт?

Оказывается, достаточно, и доказать это нетрудно. На любой правильно раскрашенной карте интересующего нас типа проведем еще одну прямую (например, жирную прямую, как на рис. 221 справа), разделив плоскость на две «карты».

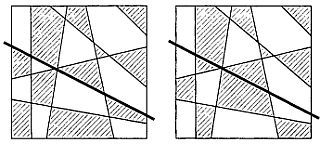
Рис. 221 Для раскраски любой карты, образованной прямыми, пересекающими всю ее поверхность от одного края листа до другого, достаточно двух красок.

Каждая из новых карт в отдельности раскрашена правильно, но к новой «границе» только что проведенной прямой примыкают пары областей, окрашенных в один и тот же цвет. Для того чтобы восстановить правильную раскраску всей карты в целом, нужно перекрасить одну из карт-половинок (какую именно — безразлично), изменив окраску каждой из областей на противоположную. То, что при этом получится, показано на рис. 221 слева. Карта над черной прямой «обращена» — перекрашена так, словно «отрицательные» области стали «положительными» и наоборот, и, как нетрудно видеть, вся карта раскрашена правильно.

Для завершения доказательства рассмотрим плоскость, разделенную на две области одной-единственной прямой. Такую карту, разумеется, можно раскрасить в два цвета. Проведем вторую прямую и раскрасим новую карту, переменив все цвета по одну сторону от новой прямой на противоположные. Затем проведем третью прямую и т. д. Ясно, что предложенный метод пригоден при любом числе прямых. Следовательно, «методом полной математической индукции» мы доказали теорему о возможности раскраски в два цвета всех карт, образованных прямыми на плоскости. Доказательство можно несколько обобщить на случай более разнообразных карт, например таких, как карта на рис. 222, образованная либо кривыми, пересекающими весь лист от одного края до другого, либо замкнутыми кривыми без самопересечений.

Рис. 222 Двух красок достаточно для раскрашивания карты, образованной либо линиями, идущими от одного края листа до другого, либо замкнутыми кривыми.

Проведя еще одну кривую, пересекающую всю карту от одного ее края до другого, мы должны, как и прежде, изменить все цвета по одну сторону от кривой на противоположные. Если вновь проведенная кривая замкнута, то изменить нужно окраску всех областей, попавших внутрь кривой, или, если угодно, всех областей, оказавшихся снаружи. Замкнутые кривые могут иметь и точки самопересечения, но в этом случае перекрашивание областей более сложно.

Заметим, что на всех приведенных здесь двухцветных картах все вершины четны (напомним, что вершиной называется точка, в которой сходятся границы более двух стран), то есть в каждой вершине сходится четное число границ. Можно показать, что любую карту на плоскости можно раскрасить в два цвета тогда и только тогда, когда все ее вершины четны. Это утверждение известно как «теорема о двухцветных картах». Нетрудно видеть, что на торе эта теорема не выполняется. Для этого достаточно скатать в трубку квадратный лист бумаги, расчерченный на девять маленьких квадратов (наподобие игрового поля для крестиков и ноликов), а концы трубки склеить. Все вершины на таком «клетчатом» торе четны, но для его раскрашивания необходимо взять три краски.

Приведем теперь (скорее для развлечения, чем для уяснения существа дела) две задачи на раскрашивание карт. Они несложны, но в каждой имеется какая-нибудь ловушка, которая делает решение не столь легким, как это кажется с первого взгляда.

1. Стифен Барр сообщил мне в письме задачу о художнике, который хочет закончить большую абстрактную картину, изображенную на рис. 223.

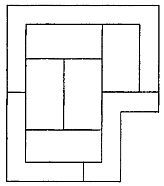
Рис. 223 Сколько красок должен взять художник, чтобы раскрасить эту абстрактную картину?

Он решил ограничиться четырьмя красками и каждую из областей окрасить только в один цвет, следя за тем, чтобы области, имеющие общую границу, не были окрашены одинаково. Площадь каждой области равна восьми квадратным футам, за исключением верхней области, имеющей вдвое большую площадь, чем остальные. Проверив запасы красок в тюбиках, художник обнаружил, что красной краски у него осталось ровно столько, сколько требуется, чтобы покрыть 24 квадратных фута, желтой хватит на покрытие такой же площади, зеленой — на 16 квадратных футов и синей — на 8 квадратных футов. Как ему следует поступить для того, чтобы закончить свою картину?

2. Известный математике Лео Мозер предложил следующую задачу: как начертить на плоскости двухцветную карту, обладающую таким свойством, что, как бы вы ни накладывали на нее равносторонний треугольник со стороной 1, все три его вершины не должны лежать на точках одного цвета?

* * *

Утверждение о том, что на плоскости нельзя начертить пять областей так, чтобы любые из них имели общую границу, было высказано в 1840 году Мёбиусом на одной из его лекций. Мёбиус придал ему форму притчи о восточном правителе, завещавшем свое царство пяти сыновьям при условии, если те сумеют так поделить наследство, чтобы владения каждого из сыновей граничили с владениями всех остальных. Эта задача эквивалентна следующей задаче из теории графов: можно ли так разместить на плоскости пять точек, чтобы они соединялись не пересекающимися друг с другом отрезками прямых? Доказательство того, что этого сделать нельзя, нетрудно, и его можно найти в любой книге по элементарной теории графов.[67]

Неточность выражений, употребленных мной при обсуждении проблемы четырех красок, как утверждения, неразрешимого в смысле Гёделя, послужила причиной следующего письма.