В какой цвет выкрасить еще не закрашенную область? Очевидно, цвет должен быть либо красным, либо каким-то новым, четвертым цветом, отличающимся от уже нанесенных на карту. Предположим, что мы избрали вторую альтернативу и выкрасили пустую область в зеленый цвет. Добавим теперь еще одну область. Вполне очевидно, что закончить раскраску карт (с соблюдением всех условий) без привлечения пятого цвета нельзя. Вернемся снова к карте и выкрасим пустую область вместо зеленого в красный цвет. Такая раскраска приводит к трудностям, если с первыми четырьмя областями соприкасаются две другие области (см. карту на рис. 219,в). Ясно, что для раскраски этих двух областей нам понадобятся четвертая и пятая краски. Является ли все сказанное доказательством того, что для раскраски некоторых карт необходимо брать пять красок?

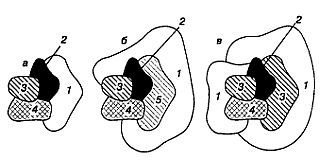
Рис. 219 При раскрашивании карты в четыре цвета часто приходится начинать всю работу сначала, выбирая другие краски. 1 — белый; 2 — черный; 3 — красный; 4 ~ серый; 5 — розовый.

Отнюдь нет. В обоих случаях мы можем обойтись всего лишь четырьмя красками, следует только вернуться к исходной карте и изменить первоначальную схему раскраски.

При раскрашивании сложных карт с десятками «стран» мы то и дело будем попадать в подобные «тупики» и возвращаться к тому, с чего начали. Следовательно, для решения проблемы четырех красок необходимо либо доказать, что во всех случаях, изменив надлежащим образом схему раскраски, можно добиться успеха, либо придумать какой-нибудь способ, который позволил бы исключить все ненужные варианты раскраски любой карты в четыре цвета. Стифен Барр предложил замечательную топологическую игру, основанную на трудности предвидения таких «тупиковых» раскрасок. Игрок А чертит произвольную область. Игрок В раскрашивает ее и пририсовывает новую область. Игрок А раскрашивает новую область и добавляет еще одну область. Игра продолжается.

Каждый из игроков раскрашивает область, начерченную противником, и дорисовывает свою область. Проигрывает тот, кто вынужден воспользоваться пятой краской. Я не знаю лучшего способа понять трудности, которые встречаются на пути решения проблемы четырех красок, чем просто поиграть в эту любопытную игру.

Часто говорят, первыми, кто понял, что для раскраски любой карты требуется взять лишь четыре краски, были картографы. Математик Кеннет О. Мэй усомнился в справедливости этого утверждения. Проведя тщательное исследование происхождения проблемы четырех красок, Мэй не нашел в старинных книгах по картографии ни формулировки проблемы, ни указания на то, что она известна авторам этих книг. По-видимому, впервые проблему четырех красок в явном виде сформулировал Фрэнсис Гетри, студент из Эдинбурга. Он упомянул о ней в письме брату Фредерику (ставшему впоследствии химиком), который в свою очередь сообщил ее (в 1852 году) своему преподавателю математику Августу де Моргану.

Широкую известность проблема четырех красок приобрела после того, как в 1878 году выдающийся математик Артур Кэли сообщил, что он размышлял над этой проблемой, но так и не сумел ее решить.

В 1879 году английский юрист и математик Альфред Кемпе опубликовал то, что, по его мнению, было решением проблемы, а год спустя представил в журнал Nature статью со сверхсамоуверенным названием «Как раскрасить карту четырьмя красками».

В течение десяти лет математики считали проблему решенной, но потом П. Дж. Хивуд указал на роковой пробел в доказательстве Кемпе. С тех пор математические умы безуспешно пытались найти решение проблемы. Внешне невинная формулировка проблемы четырех красок — кажется, что решить ее совсем нетрудно, — многим сулит ложные надежды. В своей автобиографической книге «Бывший вундеркинд» Норберт Винер писал о том, что и он, подобно всем математикам, пытался найти решение проблемы четырех красок, но каждый раз найденное решение, как заколдованное золото в волшебной сказке, обращалось в его руках в груду глиняных черепков. В настоящее время проблема четырех красок положительно решена для всех карт с числом стран, не превышающим 38. Может показаться, что 38 —очень маленькое число, но полученное решение становится менее тривиальным, если учесть, что число топологически различных карт с числом стран, не превышающим 38, оказывается больше чем 10³⁸. Даже современные быстродействующие компьютеры не в состоянии перебрать все эти варианты в сколько-нибудь разумный отрезок времени.

Отсутствие доказательства для проблемы четырех красок на плоскости становится еще удивительнее, если учесть, что аналогичные проблемы решены для более сложных поверхностей (при рассмотрении проблемы четырех красок поверхность сферы не отличается от плоскости: любую карту на сфере можно превратить в эквивалентную карту на плоскости, сферу проколоть в точке, лежащей внутри любой области, а затем растянуть на плоскости). Для раскраски односторонних поверхностей, таких, как лист Мёбиуса, бутылка Клейна и проективная плоскость, необходимо и достаточно шести красок. Для раскраски карты на поверхности тора, или бублика, число красок должно быть равно семи. Одна из таких карт показана на рис. 220,в.

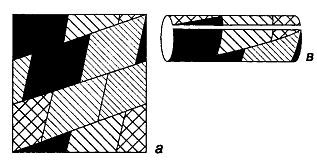
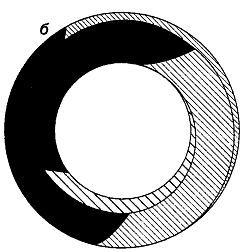
Рис. 220 Для раскраски карты на торе достаточно семи красок. Для получения тора лист бумаби (а) сворачивают в трубку (б), концы которой склеиваются (в) (тор показан в увеличенном виде).

Обратите внимание на то, что каждая область ограничена шестью отрезками прямых и примыкает к шести другим областям.

Проблема раскраски карты по сути дела решена для всех сколько-нибудь серьезно изученных сложных поверхностей, но стоит лишь взять поверхность, топологически эквивалентную плоскости или сфере, как решение проблемы ускользает от топологов. Хуже всего, что всякие видимые причины, объясняющие, почему так происходит, отсутствуют. Все предпринятые попытки, казалось, гарантировали успех, и лишь на самом последнем этапе, когда цепочка рассуждений вот-вот должна была замкнуться, обнаруживался досадный просчет, мнимый успех улетучивался подобно миражу.

Трудно заранее предсказать, каким окажется решение знаменитой проблемы, но можно не сомневаться, что того, кто первым сумеет подтвердить или опровергнуть гипотезу о возможности раскраски любой карты четырьмя красками, ожидает всемирное признание и слава. «Прорыв» в неприступной обороне проблемы может произойти по одному из трех направлений:

1. Будет начерчена карта, для раскраски которой непременно требуются пять красок. «Если взять на себя смелость и составить прогноз на будущее, — пишет Г. С. М. Коксетер в великолепной статье «Проблема четырех красок, 1840–1890 годы», — то я должен высказать предположение, что карта, требующая для своей раскраски пяти красок, вполне может существовать, но даже простейшая из таких карт имеет столько стран (их могут быть сотни и даже тысячи), что ни у кого из тех, кто столкнется с ней, не хватит терпения, чтобы проделать все необходимые проверки и исключить возможность ее раскраски с помощью четырех красок».

2. Будет обнаружено доказательство гипотезы, может быть, с помощью какого-нибудь нового метода, который внезапно откроет многие запертые двери в здании математики.

3. Будет доказано, что доказать или опровергнуть гипотезу невозможно. Это утверждение может показаться странным, но в 1931 году Курт Гёдель установил, что во всякой дедуктивной системе, достаточно сложной для того, чтобы она включала арифметику, существуют математические теоремы, «неразрешимые» в рамках этой дедуктивной системы. До сих пор удалось доказать «неразрешимость» (в смысле Гёделя) лишь очень немногих великих гипотез.