2. Каждый мяч можно поместить в углубление В, прямо над зазором между мячами первого слоя. Если придерживаться этого способа укладки мячей (при котором каждый новый мяч располатается прямо над мячом, лежащим на три слоя ниже), то в результате получается так называемая плотная кубическая упаковка.

Именно так упакованы шары, сложенные в виде четырехугольной пирамиды с боковыми гранями, имеющими форму равносторонних треугольников, и в виде тетраэдров. Различие состоит лишь в том, что в четырехугольной пирамиде слои располагаются параллельно боковым граням, а в тетраэдре — основанию.

При заполнении слоев плотной упаковки мы можем при желании переходить от гексагональной упаковки к кубической и наоборот и получать различные «гибридные» формы плотнейших упаковок. Во всех плотных упаковках — гексагональной, кубической и гибридных — каждый шар касается двенадцати соседних шаров и плотность упаковки (отношение объема, занятого шарами, к объему всего пространства) равна

или почти 75 %.

Следует ли такую плотность считать наибольшей? Более плотные упаковки неизвестны, но в статье о связи между плотной упаковкой и порами в застывшей пене (1958) Г. С. М. Коксетер высказал интригующее замечание о том, что наиболее плотная упаковка еще не найдена. Действительно, двенадцать шаров можно расположить так, что все они будут касаться одного и того же центрального шара, и лишь немногого не хватает, чтобы к этим двенадцати можно было добавить тринадцатый шар. Большие пустоты в расположении двенадцати шаров вокруг центрального шара наводят на мысль о том, что при некоторой неправильной упаковке плотность может оказаться выше 0,74… (для сравнения напомним, что при плотнейшем расположении кругов на плоскости пустот, размеры которых были бы сравнимы с диаметром круга, вообще нет). Никому еще не удалось доказать, что упаковка с плотностью, превышающей 0,74…, невозможна. Не доказано даже, что касание с двенадцатью соседними шарами необходимо для плотнейшей упаковки. Высказанная Г. С. М. Коксетером гипотеза побудила Джорджа Д. Скотта проделать ряд экспериментов с шарами, упакованными случайным образом. Он насыпал большое количество стальных шариков в сферические колбы и взвешивал их. Полученные Скоттом результаты показали, что устойчивые случайные упаковки соответствуют плотностям в диапазоне от 0,59 до 0,63. Это означает, что если упаковка с плотностью, большей 0,74…, и существует, то строить ее необходимо по тщательно продуманной схеме, которая еще никому не известна.

Приняв плотную упаковку за плотнейшую, мы сможем предложить читателю очень трудную задачу: чему равно наибольшее число стальных шариков диаметром 1 см, которые могут уместиться в квадратной коробке размером 10 х 10 х 5 см?

Если плотно упакованные круги на плоскости равномерно «раздувать» до тех пор, пока не заполнятся все промежутки между ними, то получится узор, напоминающий пол в ванной комнате, выложенный шестиугольными плитками. (Кстати сказать, этим и объясняется столь широкое распространение «шестиугольного паркета» в природе: в пчелиных сотах, в пене между двумя почти соприкасающимися плоскими поверхностями, в пигментах на сетчатке глаза, на поверхностях некоторых диатомей и т. п.) А что произойдет с плотно упакованными шарами, если их равномерно расширять в замкнутом сосуде или подвергать равномерному давлению извне? Каждый шар, оказывается, превратится в многогранник (грани которого соответствуют касательным плоскостям, проведенным в точках касания шара с соседними шарами). При кубической упаковке каждый шар превращается в ромбический додекаэдр (рис. 208, а), все двенадцать граней которого имеют вид одинаковых ромбов. При гексагональной упаковке каждый шар переходит в трапецеромбический додекаэдр (рис. 208, б), у которого шесть граней имеют вид ромбов, а другие шесть — трапеций.

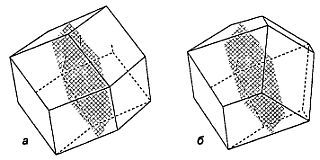
Рис. 208 При раздувании шаров, образующих плотную упаковку, они превращаются в додекаэдры.

Если трапецеромбический додекаэдр разрезать пополам показанной на рисунке плоскостью и одну из половинок повернуть на 60° относительно другой, то получится ромбический додекаэдр.

В 1727 году английский физиолог Стифен Хейлз описал в своей книге «Статистика растений» один опыт: насыпав в горшок зеленых горошин, он подверг их сжатию и получил «весьма правильные додекаэдры». Этот опыт получил название «горошин Бюффона» (потому что несколько позднее такой же опыт описал Бюффон).

У большинства биологов он не вызывал никаких сомнений до тех пор, пока Эдвин Б. Мацке, ботаник из Колумбийского университета, не повторил его. Из-за неправильной формы, неодинаковых размеров, неоднородной плотности и случайного расположения насыпанных в контейнер горошин их форма после сжатия оказалась настолько случайной, что ее трудно было отнести к какому-нибудь определенному типу многогранников. В 1939 году появилось сообщение о новых экспериментах Мацке: он сжал свинцовую дробь и обнаружил, что при кубической упаковке дробинок образуются ромбические додекаэдры, а при случайной упаковке преобладают четырнадцатигранники неправильной формы. Мацке указал, что полученные им результаты имеют важное значение для исследования таких структур, как пена или живые клетки в недифференцированных тканях.

Задача о плотнейшей упаковке наводит на мысль о прямо противоположном вопросе: какую упаковку можно назвать редчайшей, то есть при каком расположении шаров в пространстве достигается минимум плотности? Чтобы вся структура была жесткой, каждый шар должен касаться по крайней мере четырех остальных, а точки касания не должны лежать в одном полушарии или на одном экваторе. В книге «Наглядная геометрия» Д. Гильберта и С. Кон-Фоссена[62] описана упаковка, которую в то время считали редчайшей. Ее плотность составляла 0,123. Однако уже в следующем году голландские математики Г. Хееш и Ф. Лейвз сообщили подробности более редкой упаковки с плотностью всего лишь 0,0555 (рис. 209).

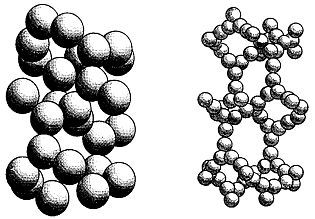
Рис. 209 Редкая упаковка Хееша и Лейвза. Большие шары сначала располагают так, как показано на левом рисунке, а затем каждый из больших шаров заменяют тремя маленькими. Результат показан на рисунке справа. Плотность такой упаковки составляет всего лишь 0,0555.

Существует ли еще более редкая упаковка? Вот еще один интересный вопрос, который так же, как и вопрос о плотнейшей упаковке, пока еще остается нерешенным.

* * *

Единственность ответа (4900 ядер) в задаче о числе шаров, которые можно уложить и в виде квадрата, и в виде четырехугольной пирамиды, была доказана Г. Н. Уотсоном A918). Предположение о единственности ответа высказал еще в 1875 году французский математик Эдуард Люка. Аналогичное предположение можно найти у Г. Дьюдени A917).

Числам, которые одновременно являются и треугольными и квадратными, посвящена обширная литература. Известна формула для n-го квадратно-треугольного числа:

Вопрос о плотнейшей решетчатой упаковке шаров решен для всех пространств, размерность которых не превышает восьми.[63] В трехмерном пространстве ответ на вопрос дают описанные нами кубическая и гексагональная упаковки с плотностью 0,74… При переходе к девятимерному пространству, как замечает К. Рейд в своей книге «Введение в высшую математику» A959), задача претерпевает одно из тех неожиданных загадочных превращений, которые столь часто встречаются в геометрии многомерных евклидовых пространств. Насколько мне известно, задача о плотнейшей упаковке гиперсфер в девятимерном пространстве никем еще не решена. Девятимерное пространство служит поворотным пунктом и в тесно связанной с проблемой упаковки задаче о числе одинаковых сфер, касающихся одной и той же сферы того же радиуса. Лишь в 1953 году К. Шютте и Б. Л. Ван-дер-Варден впервые доказали, что для трехмерного пространства ответ равен 12.[64] Более позднее доказательство можно найти в статье Дж. Лича «Задача о тринадцати сферах».[65] Соответствующая задача на плоскости имеет очевидный ответ: 6 (ровно столько одинаковых монет — но не больше! — могут касаться одной и той же монеты). Если прямую рассматривать как «вырожденную сферу», то ответ для одномерного пространства равен 2. Для четырехмерного пространства доказано, что 24 гиперсферы могут касаться одной и той же двадцать пятой гиперсферы, а для пространств размерности 5, 6, 7 и 8 максимальное число гиперсфер равно соответственно 40, 72, 126 и 240. Для девятимерного пространства задача остается нерешенной.