– Не могу отказать вам в математическом остроумии, но нахождение вывода старых формул не может подняться до значения самих этих формул. Так что я не вижу, к сожалению, смысла в вашей умственной расточительности ради повторения давно человечеством пройденного.
Пьер Ферма покраснел, потом побледнел, пронизывающе смотря на составленную им таблицу рядов, которую в эту минуту изучал арабский звездочет.
– Простите мне во имя аллаха, мои высокочтимые гости, что я рискую обратить ваше внимание на то, что в составленной молодым гостем таблице я вижу весьма примечательные особенности, которые, надо думать, он подметил и обосновал. Кроме того, можно увидеть, что тройки, вычисленные по древним формулам, не окажутся, как в таблице господина Пьера Ферма, простейшими числами. Произвольно задаваясь величинам m и n, мы получим после вычислений хаотические, беспорядочные, как россыпь разноцветных камней, значения всевозможных прямоугольных треугольников, отнюдь не способствующих выявлению законов их построения.
– Вы правы, уважаемый Мохаммед эль Кашти, таблица троек действительно дает возможность установить некоторые зависимости как в вертикальных рядах, так и в рядах, соседствующих по горизонтали. – И он познакомил слушателей с тем, что открыл[16].
По просьбе арабского ученого особенно остановился Пьер Ферма на выборе коэффициента α и β в своих формулах.
– Вас интересует, уважаемый Мохаммед эль Кашти, случай, когда коэффициенты α и β содержат общий множитель √21? – И он показал с убедительной простотой, что в этом случае получающиеся тройки будут повторять все первые тройки соседних по горизонтали рядов[17].
– Вы убедили меня, почтенный знаток и поэт чисел. Видит аллах, с каким благоговением я стараюсь вникнуть в найденные вами числа и мудро расставленные по клеткам таблицы, кажущейся мне поистине волшебной. Но я покажу почтенным господам, какие тайны хранит в себе эта простенькая таблица.
– Что же вы обнаружили в ней, уважаемый Мохаммед эль Кашти? Разве я не все понял в собственной работе?
– Конечно, не все, ибо все понятно лишь одному всемогущему аллаху! Но достаточно прикоснуться к математическому сокровищу, чтобы обнаружить в нем…
– Что же? Что? – нетерпеливо торопил арабского звездочета Пьер Ферма.
– Благословенное аллахом золотое сечение! 8 единиц рассекаются на 5 и 3, 13 – на 8 и 5! А эти цифры стоят в таблице поблизости, как и в орнаменте[18]!
Декарт скептически пожал плечами и поморщился. Араб воскликнул:
– Видит аллах справедливый, что вы напрасно так холодны, господин Картезиус! В этой премудрой таблице египетских рядов, как в бездонном колодце, можно черпать сокровища знаний.
– Я не хочу отказывать древним в важных познаниях, но я не вижу причин искать закономерности построения треугольников, будучи не уверен в их практической ценности, поскольку величины сторон ограничены такой условностью, как целочисленность.
– О многочтимый господин Картезиус! Я с почтительным вниманием изучаю ваши латинские труды по философии, стараясь вникнуть в глубину ваших мыслей, но позвольте возразить вам, не оспаривая вашего права на высказанное мнение.
– Пожалуйста, прошу вас, почтенный Мохаммед эль Кашти.
– По вашему определению, господин Картезиус, человек начал существовать как человек, лишь обретя способность мыслить, а это произошло тогда, когда он стал считать по пальцам, определять, сколько плодов он сорвал, сколько дичи принес, сколько членов его семьи или племени должны его добычу разделить между собой. По-латыни, как вы знаете, «вычисление – калькуляция» происходит от слова calculus, что означает «камешек», число камешков могло быть только целым. И в нашей жизни, начиная от числа людей, быков, кораблей, домов и окон в них, кончая числом звезд в созвездиях, – все это только целые числа. Природа по воле аллаха не знает дробей.
– Но при чем тут закон Природы, созданной всевышним, и прямоугольные треугольники? – с вызовом спросил французский философ.
– Величайшая тайна творения, уважаемый мною господин Картезиус, как я верю и убежден, заключена в том, что первородный закон Природы и ее творца до необычайности прост, не менее прост, чем открытый Пифагором закон прямоугольного треугольника. И неспроста древние египтяне после разлива Нила вновь разбивали поля с помощью веревки с узлами через три, четыре и пять мер, натягивая ее на три колышка и получая очень точно необходимый им прямой угол. А как такие прямые углы нужны морякам, определяющим свое местонахождение по звездам, или нам, звездочетам, эти звезды изучающим? И кто возьмется сказать сейчас, как еще послужат людям сведенные в эту таблицу прямоугольные треугольники?
Конечно, маленький арабский звездочет был только человеком своего времени, невежественным астрологом, пытающимся предсказывать будущее по расположению звезд, но в этой реплике, сказанной двум выдающимся ученым XVII века о простоте первородных законов Природы, он, сам того не подозревая, поднялся до поистине гениальных высот предвидения. Мог ли он даже предположить, что другой великий ученый, которому жить триста лет спустя, в XX веке, создаст теорию относительности, из которой последует[19], что для летящего с субсветовой скоростью тела гипотенуза прямоугольного треугольника представит увеличивающуюся массу тела, его энергию и собственное время, в то время как горизонтальный катет – массу, энергию и время покоя, а вертикальный катет будет отличаться от гипотенузы так же, как и скорость тела от скорости света, длина же тела сократится по тому же закону.
Никто из присутствующих не знал глубин характера Пьера Ферма, в котором сочеталась доброта и скромность с уверенностью в неограниченности своих возможностей. Он считал, что ему доступно все на свете и в языкознании, и в поэзии, и в изучаемом праве, и в полюбившейся ему математике, никто не ожидал и не мог бы объяснить его неожиданный поступок. Пьеру Ферма было совершенно достаточно собственного признания того, что он не напрасно искал и нашел закономерности простейших пифагоровых троек, он был искренне восхищен увлеченностью его работой арабского ученого, чрезвычайно ему симпатичного, он хотел еще показать своему соотечественнику Рене Декарту, что он тоже способен на победу над самим собой. И Пьер Ферма сделал то, что стало обычным в его последующей научной деятельности, ему всегда казалось достаточным найти, открыть самому, а потом, не делая и не записывая даже выводов, предлагать своим современникам пройти его путем. Была ли это гордыня или скромность гения, но, как бы то ни было, Пьер Ферма и в последующие годы не оформлял своих трудов, не издавал собрания сочинений, не разыскал собственных найденных им доказательств (или не записал их!).
А сейчас он поразил и маленького арабского звездочета, и Декарта обращенной к ним речью:
– Я глубоко признателен вам, уважаемый Рене, за заботу о полезном применении моих способностей. За один сегодняшний день вы дали мне два урока: как победить самого себя и как бережно расходовать свои силы. А вам, досточтимый Мохаммед эль Кашти, я благодарен за то, что своей оценкой моей скромной работы вы открыли мне глаза на мою слепоту, показали мне тайны, мимо которых я проходил. Вы усмотрели в восстановленной мной египетской таблице пифагоровых чисел такой сокровенный смысл, что я не могу больше считать ее своей, она – ваша! Только вы, истинный поэт чисел, сможете увидеть в ней то, что откроется будущим поколениям. В моей памяти останется лишь формула, стоившая Пифагору сотню быков, а мне – размышлений о величине в степени, которую можно разложить на два слагаемых в той же степени.
И с этими словами Пьер Ферма торжественно передал арабскому ученому свои вычисления, сведенные в таблицу.
Мохаммед эль Кашти застыл ошеломленный. Декарт же пытался разобраться в поступке молодого соотечественника: кто он? Гордец или скромник? Гений или воплощение беспечности?
16
Примечание автора для особо интересующихся.
Вертикальные ряды x представляют собой арифметические прогрессии с показателем = 2β. Все значения сторон треугольников с возрастанием ряда изменяются по арифметической прогрессии, показатель которой для y – постоянен и равен 4, а для x и z увеличивается с порядковым номером ряда и порядкового номера тройки в вертикальном ряду и равен 4 (β + i – 1), где i – порядковый номер тройки в ряду.
17
Примечание автора для особо интересующихся. Золотое сечение было известно древним зодчим, но сформулировано Леонардо да Винчи. Цифры 3, 5, 8, 13 совпадают с частью ряда Фибаначчи, помогающего современным ученым объяснять ряд явлений природы (1, 1, 2, [3, 5, 8, 13], 21, 34 и т. д.).
18
Примечание автора для особо интересующихся. Если α = p√2e, β = q√2e, то p и q могут быть и четными и нечетными, x = α β = 2pqe, y = (p2 – q2) e; z = (p2 + q2) e, то есть p и q тождественны m и n древних формул (см. пред. примеч.), x и y просто меняются местами, к тому же, помноженные на e, не являются простейшими.
19
Примечание автора для особо интересующихся. По теории Эйнштейна, масса тела m, летящего со скоростью v при массе покоя m0 и скорости света C, меняются по формуле
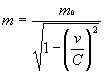
Это выражение легко преобразуется в
или графически в Δ.
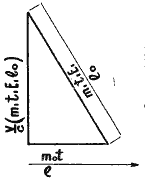
Тот же закон прямоугольного треугольника отражен и в сокращении длины покоящегося тела l0 до l в полете, и парадоксе времени теории относительности (преобразования Лоренца) при t0 – прошедшее время неподвижного наблюдателя, t – время на улетевшем от него объекте и C – скорость света:
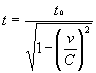
или
– опять Δ.
Сокращение наблюдаемой с неподвижной точки длины летящего тела l по сравнению с длиной его в состоянии покоя – l0:
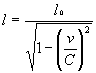
или
– опять Δ.
И наконец, тот же закон скажется и на энергии летящего тела E при энергии его покоя E0:
– Δ. Таким образом, все парадоксальные эффекты теории относительности подчинены основному закону Пифагора.