– Как я догадываюсь, не понимая благозвучного языка своих гостей, – вмешался на знакомой всем латыни хозяин дома, – почтенный господин Картезиус хотел бы говорить с моим молодым французским гостем о поединке?
– Вы правы, уважаемые господа, я намереваюсь говорить с бакалавром Пьером Ферма о нашем несостоявшемся поединке.
– Но это невозможно, да подтвердит это аллах! – воздел руки к небу маленький араб.
– Но я ничего не имею против этого, – послышался голос Пьера, – я сам хотел отыскать господина Декарта, если бы неожиданное математическое увлечение не помешало мне.
– И совершенно напрасно, – отрезал Декарт, – ибо право говорить об этом первому принадлежит мне, и я не намерен его уступать.
– Почему же? – искренне удивился Пьер Ферма.
Маленький араб понял, что он погиб, ибо сейчас этот свирепый офицер с наружностью льва вызовет на поединок беззащитного юношу, чтобы убить его, после чего не спастись от гнева османского паши и ему, Мохаммеду эль Кашти.
– Почему? – переспросил Декарт. – Да потому, милостивый государь, что право первому говорить о несостоявшемся поединке принадлежит мне, офицеру гвардии короля Франции, которому я служу, как и его высокопреосвященству господину кардиналу, и по этому праву я и явился к вам сюда, дабы принести извинение за свое недостойное поведение на кладбище у могилы великого Диофанта, и я, Рене Декарт, почтительно прошу извинить мою непростительную вспыльчивость, вызванную лишь преклонением перед прахом великого ученого древности.
Все это Декарт произнес на латинском языке, чтобы хозяин дома мог понять его. И Мохаммед эль Кашти, и метр Доминик Ферма оба не верили ушам, пораженные покаянными словами и одновременно грозным видом офицера.
– Нет большего воздаяния аллаху, чем прекращение вражды! – вымолвил наконец маленький араб. – Надо думать, господину Картезиусу удалось найти предложенное молодым Ферма решение уравнения по двум его членам вместо семи, что и привело его к столь благородному поступку?
– Вы ошибаетесь, почтенный Мохаммед эль Кашти. Рене Декарт, которого вы видите перед собой, никогда не нарушит данной им клятвы и не станет искать решения уравнения, о котором вы изволили вспомнить. Такой исход оказался бы самым простым, но недостойным той внутренней борьбы, которую мне привелось выдержать, чтобы победить недостойную мыслителя дворянскую спесь и решиться на этот визит с принесением извинений как господину Пьеру Ферма, так и его отцу метру Доминику Ферма и гостеприимному нашему хозяину на александрийской земле Мохаммеду эль Кашти. Я искренне сожалею не только о своей вспыльчивости, но также и о данной мной клятве, которую не могу нарушить, хотя мне очень хотелось бы узнать блестящее решение уравнения по двум членам из семи, но, поверьте, этого я сделать не могу.
– То, что сделали вы, уважаемый Рене Декарт, значительно больше нахождения решения[12], на которое я случайно напал, переводя могильную надпись. Не сомневаюсь, что вам не составило бы труда это сделать, если б не ваш собственный запрет, заслуживающий всяческого уважения, – произнес Пьер Ферма, восхищенно глядя на философа в офицерском мундире. Он вспомнил о прочитанных им трудах Картезиуса, о беседе с ним за шахматной доской во время плавания на фелюге и понял, какой внутренней борьбы стоило Декарту прийти сюда с извинениями. – Я понимаю вас и хотел бы отплатить вам тем же, признав легкомысленным свое предложение найти иное решение уравнения, написанного вашей шпагой на песке. Я сожалею об этом и признаю вас несоизмеримо сильнее себя, ибо нет победы большей, чем победа над самим собой.
– Вот вам моя рука, Пьер, мой друг, я всегда буду гордиться не только этой минутой торжества над тем, что надлежит неустанно искоренять, но и знакомством с вами и переходом теперь на обращение ко мне – просто Рене.
Мохаммед эль Кашти не воспринял этой прочувствованной французской речи, но прекрасно понял значение того рукопожатия, которым обменялись между собой Рене и Пьер.
– Слава аллаху, слава аллаху! – только и мог пробормотать он.
– Да возрадуется святой Доминик, чьи молитвы заступника дошли до всевышнего! – вторил ему метр Доминик Ферма.
– Если Рене, мой друг, почтит вниманием некоторые мои «математические этюды», как мне хочется их назвать, то я буду счастлив, хотя они касаются всего лишь прямоугольных треугольников, а не проблем души и тела.
– С охотой, Пьер, мой друг. Я всегда верил, что математика в конце концов привлечет вас к себе, ибо нет, кроме нее, более организующего начала.
– Представьте себе, Рене, – говорил Пьер Ферма, ведя Декарта в свою рабочую комнату, – я больше всего сожалел в последние дни, что не могу из-за нашей размолвки познакомить вас со своими этюдами.
По дороге Пьеру и Рене попался извивающийся из желания угодить Огюст, но он исчез, едва Декарт посмотрел на него.
Оба француза сели за стол у стрельчатого окна, защищенного от солнца пышной зеленью сада. Здесь жара не ощущалась такой невыносимой, как в другом месте.
– Итак, с чем же вы, мой друг, хотите познакомить меня? Из-за чего вы жалели о нашей размолвке?
– Прежде всего с тем, что формула Пифагора заключает в себе строго организованные ряды простейших пифагоровых троек, то есть значений сторон прямоугольных треугольников, не имеющих общего делителя.
– Любопытно. Как же вы это доказываете, мой друг?
– Позвольте и мне, уважаемые гости Аль-Искандарии, ознакомиться с выводами молодого ученого, – попросил вошедший вслед за Пьером и Декартом хозяин дома.
– Охотно, уважаемый Мохаммед эль Кашти, тем более что вы послужили толчком для всех находок, которые я могу показать, – живо отозвался Пьер Ферма.
– О, слава аллаху, моя помощь в этом высоком деле ничтожно мала, я обратил ваше внимание лишь на то, чего не видел сам.
– Я сожалею, что не пришел извиниться сразу, тогда мы смогли бы вместе повидать необычный орнамент, о котором я уже услышал через Огюста, но я надеюсь, что наш друг возместит упущенное, – произнес Декарт, поклонившись в сторону Пьера Ферма.
И тот стал увлеченно показывать сделанные им преобразования формулы Пифагора[13].
Декарт внимательно выслушал Пьера Ферма, взял в руки составленную им таблицу, лицо его из грозного стало сосредоточенным, потом он горько усмехнулся:
– Друг мой, боюсь разочаровать вас, но стоило ли вам вкладывать столько труда в «изобретение колесницы», известной еще при фараонах?
– Вы правы, Рене, очевидно, при фараонах жрецы бога Тота знали эти ряды, но разве не наш долг вернуть людям утраченные знания?
– Вы не поняли меня, друг мой. Я применил метафору о колеснице, имея в виду, что она известна была и древним римлянам, даже в наше время на ее основе созданы кареты. Просто вам нет надобности применять свой математический дар для вычисления сторон приевшихся всем прямоугольников, поскольку древние оставили нам изящные формулы, дающие значения всех возможных пифагоровых троек. – И он размашисто написал на листе несколько формул. – Их связывают чуть ли не с Платоном, их можно найти в X книге «Начал» Евклида[14].
– Простите, что я вступаю в ваш высоконаучный разговор, почтенные знатоки чисел, – вмешался звездочет, – но арабской науке действительно известны эти древние формулы, правда, в несколько другом написании. Однако, к сожалению, до нас не дошел их вывод. Впрочем, в том, что они дают верный результат, я имел, по воле аллаха, возможность убедиться всякий раз, когда их применял, подобно тому, как это делал сам Диофант.
Пьер Ферма нахмурился, пристально глядя на свои и написанные Декартом формулы:
– Они выводятся очень просто, почтенные господа, из тех самых выражений, которые позволили мне составить таблицу. – И Пьер Ферма показал, как удивительно простым способом можно получить эти древние формулы[15].
12
Решение это таково: если согласно четвертой и пятой строчкам надписи число прожитых Диофантом лет делится и на 12 и на 7, то возраст его будет равен 12·7 = 84 (или 168, что исключено). Возможно, надпись и предусматривала составление неопределенного Диофантова уравнения с тремя (а не с семью в определенном уравнении) членами:
где «y» теоретически не может быть больше 19, чтобы «x» получился бы величиной целочисленной и реальной для человеческого возраста. Очевидно, в этом и подразумевалась мудрость искусства покойного математика. (Примеч. авт.)
13
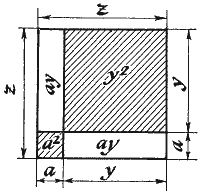
Примечание автора для особо интересующихся. Если, как следует из квадрата орнамента, z = y + a, то z2 = x2 + y2 будет иметь вид z2 = y2 + (a2 + 2ay) и x2 = a (a + 2y). Если a = a2 и (a + 2y) = b2 то x = ab, y = (a2 – b2) / 2; z = (a2 + b2) / 2.
Из выражения для «y», где в числителе разность квадратов a и b, ясно, что хотя бы одна из этих величин не может быть четной, иначе «y» не будет целым числом. Случай с иррациональными числами рассмотрен в последующем примечании.
Для возрастающих коэффициентов a и b можно составить таблицу, из которой вытекает ряд закономерностей, в частности формулировка новой теоремы. Нечетный катет простейших пифагоровых троек в целых числах разлагается на два взаимно простых сомножителя, квадраты которых соответственно равны сумме или разности гипотенузы и второго катета, то есть в дополнение к теореме Пифагора: a2 = z – y; b2 = z + y.

(В приводимой таблице цифры в скобках получены после сокращения намеченного в таблице значения на общий множитель и равны цифрам столбца при β = 1.)
14
x = m2 – n2; y = 2mn; z = m2 + n2. (Примеч. авт.)
15
Примечание автора для особо интересующихся.
Если положить a = m + n; b = m – n, то x = ab = (m + n) (m – n) = m2 – n2; y = 2mn; z = m2 + n2, что и было записано Декартом.