Мы приводим на рисунке эту странную итоговую позицию. Легко заметить, что ни одна белая фигура не может ходить.

177. Ходите следующим образом:

Разумеется, под «королевским рядом» понимается горизонталь, на которой король находился первоначально. Хотя если черные будут играть плохо, то могут получить мат за меньшее число ходов. Выше учтены все возможные ходы черных.

178.

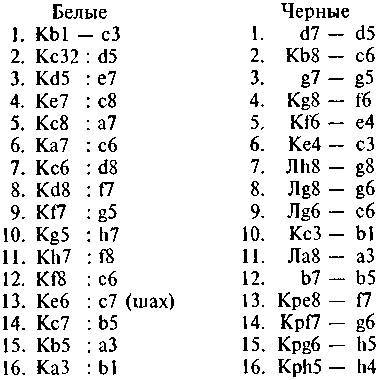
Теперь белые дают мат в три хода. .

17. d2 — d4 17. Kph4 — h5

18. Фd1 — d3 18. Kp ходит

19. Фd3 — h3 (мат)

Если

18. е2 — е4 (шах) 17. Kph4 — g3

19. g2 — g3 (мат) 18. Kp ходит

Данная позиция после шестнадцатого хода с матом в три хода впервые была дана С. Лойдом в его книге «Шахматные орешки».

179.

1. Kgl — f3

2. Кf3 — h4

3. Кh4 — g6

4. Kg6 : h8

5. Kh8 : g6

6. Kg6 : f8

7. Kpe8 : g8

8. Кb1 — c3

9. Kc3 — a4

10. Ka4 — b6

11. Kb6 : a8

12. Ka8 : b6

13. Kb6 : c8

14. Kc8 : d6

15. Ф61 — e1

16. Kd6 : e8

17. Король берет коня, и мы получаем искомую позицию.

Черные в точности повторяют ходы белых, поэтому выше приведены лишь ходы последних. В партии число ходов (17) наименьшее возможное.

180. Расположите 8 оставшихся белых фигур следующим образом: Кр на f4, Ф — b6, Л — d6, Л — g7, С — d5, С — h8, К — а5 и К на с5. При этом можно получить следующее количество матов:

Открывая Ф 8

Открывая Л на d6 13

Открывая С на b8 11

Слоном на а5 2

Пешками 2

Итого: 36

Возможно ли придумать позицию, при которой за один ход можно было бы дать более 36 различных матов? Насколько мне известно, никому еще не удалось превзойти мое решение.

181. Мистер Блэк оставил своего короля на клетке g2, и, какую бы фигуру Уайт ни выбрал вместо своей пешки, ему не удастся поставить Блэку мат. Как мы уже сказали, черный король не обращает внимания на шахи и никогда не двигается с места. Уайт может, проведя пешку на восьмую горизонталь, заменить ее ферзем, взять черную ладью и атаковать тремя своими фигурами, но мат совершенно невозможен. На любой другой клетке мат для черного короля оказался бы возможным. Сэм Лойд первым указал на ту странную особенность, на которой основана данная головоломка.

182. Переместите белую пешку с f6 на е4 и поставьте черную пешку на П. Теперь белые ходят пешкой на е5, шах, и черные должны ходить пешкой на f5. Тогда белые ходят пешкой, берут, проходя, пешку, шах и мат. Следовательно, белые сделали ход последними и привели к данной позиции. Это единственное возможное решение.

183. Если вы расположите фигуры так, как показано на рисунке (где изображен только нужный участок доски), то черному королю будет сделан шах, а ходить ему некуда. Читатель видит теперь, почему я избегал термина «мат». Помимо того, что отсутствует белый король, данная позиция невозможна в реальной шахматной игре, ибо белые не могут сделать черным шах двумя ладьями одновременно, а черный король также на последнем шаге не может занять позицию под шахом.

Я полагаю, что эта позиция была впервые опубликована Сэмом Лойдом.

184. Ходите следующим образом:

1. Лс6 — d6 2. Крbб — а7 3. Ла6 — с6 (мат).

Черные делают вынужденные ходы, которые не нужно указывать.

185. Общая формула для шести пешек на квадратных досках, больших 2×2, такова: ушестеренный квадрат числа сочетаний из n предметов по 3, где n — число клеток на одной стороне доски. Разумеется, если п четно, то и число незанятых клеток в одном ряду должно быть четным, а если n — нечетно, то и число незанятых клеток обязано быть нечетным. В нашем случае n = 8, так что ответ равен 18 816. Это иная форма уже знакомой головоломки 27. Я повторяю ее здесь, чтобы объяснить метод решения, доступный новичку. Прежде всего очевидно, что если мы поставим пешку на любую прямую, то должны поставить на эту же прямую еще одну пешку, дабы число пустующих клеток оказалось четным. Мы не можем поставить в одной горизонтали 4 или 6 пешек, ибо в соответствующих вертикалях не удалось бы тогда обеспечить четное число пустующих клеток. Следовательно, мы должны поставить по две пешки в каждую из трех горизонталей и в каждую из трех вертикалей. Далее, при этих условиях существует всего 6 схем расположения, указанных на рисунке.

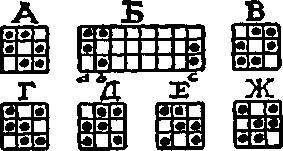
Я только упомяну, что А и Г — единственные два существенно различных расположения, поскольку если вы повернете А на четверть оборота, то получите В, а если вы станете поворачивать Г на четверть оборота по часовой стрелке, то получите последовательно Д, Е и Ж. Не важно, как вы располагаете свои пешки; если удовлетворяются условия головоломки, то вы обязательно получите одно из этих расположений. Разумеется, мы понимаем, что простое расширение не нарушает существенно характера этих расположений. Так, Б есть всего лишь расширенная форма А. Решение, следовательно, состоит в отыскании числа таких расширений. Предположим, что мы ограничились первыми тремя горизонталями, как в случае Б; тогда, поместив пары а и b на первых двух вертикалях, мы можем пару с расположить на любой из шести остальных вертикалей, что даст 6 решений. Теперь сдвинем пару b на третью вертикаль; тогда для пары с останется 5 возможных положений. Сдвинув b на четвертую вертикаль, мы оставим для с 4 возможности и так далее до тех пор (где а по-прежнему находится на первой вертикали), пока мы не сдвинем b на седьмую вертикаль, оставив для с единственное место на восьмой вертикали. Затем мы можем поместить а на второй, b на третьей, а с на четвертой вертикали и, сдвигая, как и прежде, с и b, находить серии новых решений.

Таким образом, мы получаем, что, пользуясь лишь схемой А и ограничивая себя только тремя верхними горизонталями, мы получаем столько ответов, сколько есть сочетании из 8 предметов по 3, то есть

. Читатель сразу же догадается, что если можно 56 способами выбрать вертикали, то ровно столькими же способами в каждом из этих случаев можно выбрать горизонтали, ибо мы можем сдвигать пару сверху вниз точно так же, как и слева направо. Следовательно, общее число способов, подчиняющихся схеме А, равно 56 × 56 = 3136. Но, как мы уже видели ранее, существует 6 различных схем. Поэтому ответ равен 3136 × 6 = 18 816, как я и утверждал.

186. Ходите следующим образом: 3—11, 9—10, 1—2, 7—15, 8—16, 8—7, 5—13, 1—4, 8—5, 6—14, 3—8, 6—3, 6—12, 1—6, 1—9, и все шашки оказываются удаленными, за исключением 1, что и требовалось в условиях задачи.

187. Ходите следующим образом: 7—15, 8—16, 8—7, 2—10, 1—9, 1—2, 5—13, 3—4, 6—3, 11—1, 14—8, 6—12, 5—6, 5—11, 31—23, 32—24, 32—31, 26—18, 25—17, 25—26, 22—32, 14—22, 29—21, 14—29, 27—28, 30—27, 25—14, 30—20, 25—30, 25—5. Две оставшиеся шашки — это 25 и 19, обе они принадлежат к одной группе, как и требовалось, причем 19 ни разу не сдвигается со своего исходного положения.

Я думаю, что невозможно придумать решение, где бы в конце игры на доске осталась только одна шашка.

188.

Белые

Черные

1.

f2 — f4

1.

c7 — c6

2.

Kpel —12

2.

Фd8 — a5

3.

Kpf2 — e3

3.

Kpe8 — d8

4.

f4 — f5

4.

Kpd8 — c7

5.

Фd1 — c1

5.

Kpc7 — b6

6.

Фe1 — g3

6.

Kb8 — a6