136. Фишки можно расположить в следующем порядке:

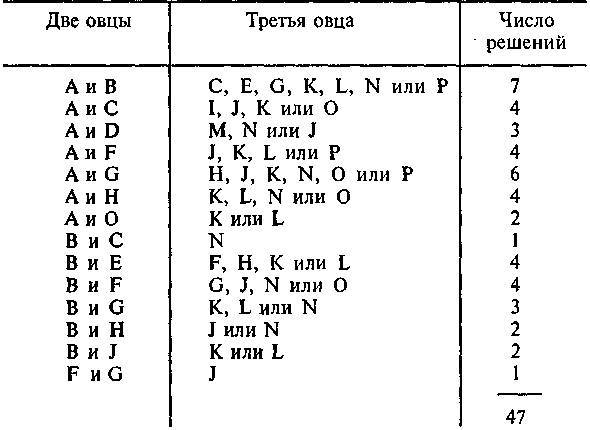
137. Число различных расположений овец по загонам, при которых каждый загон либо оказывается занятым, либо находится на одной вертикали, горизонтали или диагонали по крайней мере с одной овцой, равно 47.
В таблице указаны все эти расположения, разобраться в которых поможет ключ из рисунка 1.
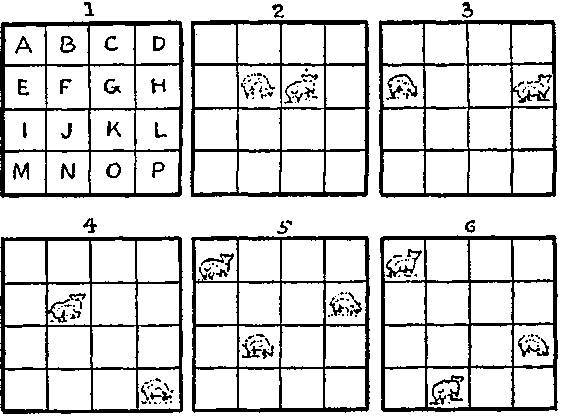
Это, разумеется, означает, что если вы поместите овец в загоны А и В, то существует 7 различных загонов, куда вы сможете поместить третью овцу, что дает 7 различных решений. Мы помним, что повороты и отражения не приводят к новым решениям.
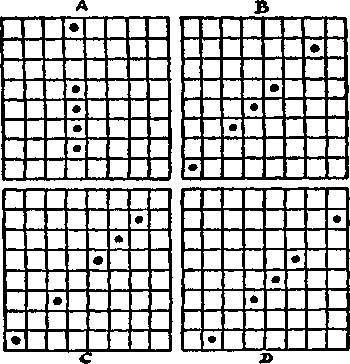
Если потребовать, чтобы по крайней мере один загон не находился на одной прямой ни с какой овцой, то число решений окажется равным 30. Если мы в каждом из этих 47 и 30 случаев соответственно будем считать новыми решения, получающиеся с помощью поворотов и отражений, то получим общее число решений, равное 560, что совпадает с числом способов, которыми овец можно разместить по трем загонам вообще без всяких условий. Я хочу отметить, что существуют три способа, какими можно двух овец расположить так, чтобы каждый загон либо оказался занятым, либо находился на одной прямой по крайней мере с одной овцой (см. рисунки 2, 3 и 4), но при этом в каждом случае овцы располагаются на одной прямой. Существуют лишь 2 расположения, при которых каждый загон оказывается либо занят, либо на одной прямой по крайней мере с одной овцой, но никакие две овцы не располагаются на одной прямой друг с другом (см. рисунки 5 и 6). Наконец, существует лишь один способ, при котором три овцы располагаются таким образом, что по крайней мере один загон не находится ни на какой прямой ни с одной овцой и никакая овца не находится на одной прямой с другой овцой. Поместите овец в клетки С, Е и L. Этим практически исчерпывается все, что следовало бы сказать по поводу такого приятного пасторального сюжета.
138. На рисунке показаны 4 фундаментально различных решения. В случае А мы можем изменить порядок так, чтобы одиночная собака оказалась внизу, а остальные отстояли от нее на 2 клетки вверх. Точно так же мы можем использовать следующую справа вертикаль и обе из двух центральных горизонталей. Таким образом, случай А порождает 8 решений. Далее, решение В можно повернуть на 180° и расположить вдоль любой диагонали, что дает 4 решения. Аналогично случай С дает 4 решения. Расположение на прямой в случае D симметрично, так что повороты на 180° ничего нового не дадут, но собак можно помещать вдоль 4 различных прямых. Таким образом, мы получаем всего 20 различных решений.
139. Если бы древний архитектор расположил 5 своих полумесяцев так, как показано на рисунке, то каждая плитка оказалась бы под наблюдением (то есть на одной прямой) по крайней мере одного полумесяца и, кроме того, осталось бы место для квадратного ковра, занимающего ровно половину всего данного участка пола. Весьма удивительно, что, хотя существуют 2 или 3 решения, при которых ковер, если соблюдаются все прочие условия, занимает площадь приблизительно в 29 плиток, это единственно возможное решение, дающее ровно половину всей площади, что является максимумом.

140. Слон находится на клетке, занятой первоначально ладьей, а 4 ферзя расположены таким образом, что каждая клетка либо занята, либо оказывается под угрозой нападения одной из фигур (см. рисунок а).
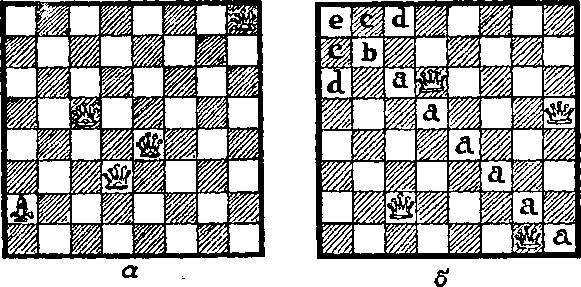
Если 4 ферзя расположены, как показано на рисунке б, то пятого ферзя можно поместить на любую из 12 клеток, помеченных буквами a, b, с, d и е; либо можно поставить ладью на две клетки с; либо слона на 8 клеток а, b и е; либо пешку на клетку b; либо короля на четыре клетки b, с и е. Единственное известное расположение четырех ферзей и коня, принадлежащее Дж. Уоллису, приведено на рисунке в.
Я нашел большое число решений для случая четырех ферзей и ладьи или слона, но единственным решением, как я полагаю, с тремя ферзями и двумя ладьями, при котором все фигуры защищены, будет решение (см. рисунок г), впервые опубликованное доктором К. Плэнком. Однако с тех пор я нашел дополнительное решение для случая трех ферзей, ладьи и слона, хотя фигуры и не защищают друг друга (см. рисунок д).

141. Мои читатели привыкли к тому, что требуется по меньшей мере 5 планет, дабы атаковать каждую из 64 звезд, расположенных в виде квадрата, а потому многие из них, быть может, полагают, что в случае большего квадрата потребуется увеличить число планет. Именно с целью изменить это ошибочное мнение, а также предостеречь читателей от еще одного из тех многочисленных подводных камней, которыми полон мир головоломок, я и придумал эту новую задачу со звездами. Позвольте мне сразу же заметить, что в случае квадратного расположения 81 звезды существует несколько искомых расположений. На рисунке приведено решение головоломки «Южный Крест».

Стоит вспомнить, что в условии говорилось: «Разумеется, после перестановки они закроют 5 новых звезд, отличных от тех, которые закрыты сейчас». Это было сделано для того, чтобы исключить более простое решение, в котором передвигаются лишь 4 планеты.
142. Передвижения ферзей ясны из приведенных здесь рисунков 1—4, которые показывают положение на доске после каждого перемещения. В итоге все клетки оказываются либо занятыми, либо под ударом, но ни один ферзь не угрожает другому ферзю. На последнем шаге ферзя в верхнем ряду можно было бы передвинуть еще на одну клетку дальше влево. Это, как я полагаю, единственное решение данной головоломки.
143. На рисунке можно заметить, что только 3 ферзя передвинуты с их первоначального положения на краю доски и что в результате 11 клеток (отмеченных черными точками) не находятся под угрозой нападения. Я рискну утверждать, что 8 ферзей нельзя расположить на шахматной доске таким образом, чтобы остались неатакованными более чем 11 клеток. И хотя строгое доказательство этого факта отсутствует, я полностью уверен в справедливости данного утверждения. Существует по меньшей мере 5 различных расположений, при которых остаются неатакованными 11 клеток.

144. Шестнадцать пешек можно расположить таким образом, чтобы никакие три из них не оказались на одной прямой, идущей в любом направлении (см. рисунок). Как и требовалось в условии, мы рассматриваем пешки просто как точки на плоскости.

145. Существует 6480 способов, которыми можно разместить человека и льва при единственном ограничении, что они располагаются в разных местах. Это очевидно, ибо человека можно поставить на любое из 81 места, и в каждом случае остается 80 мест для льва; следовательно, 81 х 80 = 6480. Далее: если мы вычтем отсюда число способов, при которых человек и лев оказываются на одной тропе, то в результате получится число способов, при которых они не располагаются на одной тропе. Число способов, при которых они оказываются на одной тропе, равно, как можно установить без особых затруднений, 816. Следовательно, искомый ответ равен 6480 — 816 = 5664.
Решением в общем случае будет