Это, разумеется, эквивалентно тому, как если бы мы сказали, что при условии, что на стороне шахматной доски расположено n клеток, на ней можно разместить двух слонов указанным числом способов, при которых они не атакуют друг друга. Только в таком случае ответ нужно было бы уменьшить вдвое, поскольку два слона не отличаются друг от друга, и, поменяв их местами, мы не получим нового решения.

146. Наименьшее возможное число коней при данных условиях равно 14. Иногда полагают, что существует очень много различных решений. Кстати, существуют лишь 3 расположения, если не учитывать повороты и отражения. Довольно удивительно, что, по-видимому, никому в голову не пришло следующее простое доказательство и никто не догадался действовать с белыми и черными клетками по отдельности.

Семь коней можно расположить на белых клетках так, чтобы они атаковали каждую черную клетку лишь двумя способами. Они показаны на рисунках 1 и 2. Обратите внимание, что в обоих случаях 3 коня занимают одинаковые положения.

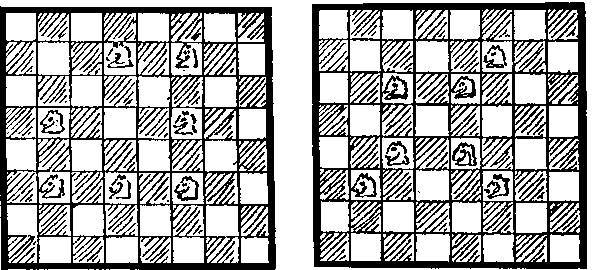
Следовательно, ясно, что если вы повернете доску так, чтобы в левом верхнем углу оказалась черная клетка, и поставите коней на те же самые места, то у вас получатся два похожих способа атаки всех белых квадратов. Я предположу, что читатель выполнил два последних описанных рисунка на кальке, и обозначу их 1а и 2а. Теперь, наложив рисунок 1а на рисунок 1, вы получите решение на рисунке 3, наложив рисунок 2а на рисунок 2, вы получите рисунок 4, а наложив рисунок 2а на рисунок 1, получите рисунок 5.

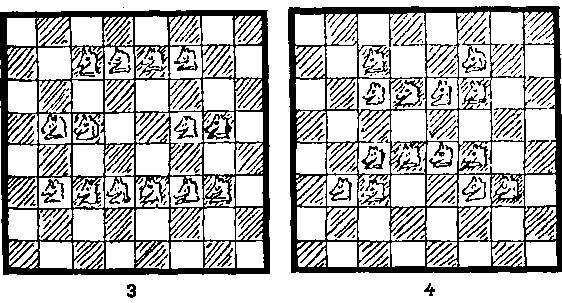
Вы можете теперь перебрать все возможные комбинации этих двух пар рисунков, и при этом вы получите лишь те 3 решения, которые я привел, а также решения, получающиеся из них с помощью поворотов и отражений. Следовательно, существуют только эти 3 решения.

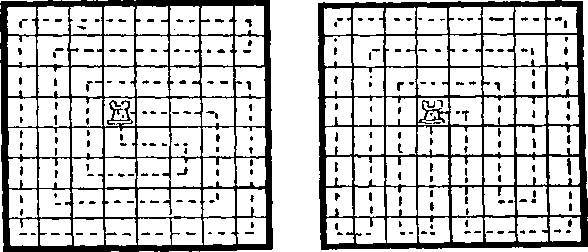
147. Два единственно возможных минимальных решения приведены на двух рисунках, где, как можно заметить, требуется лишь 16 ходов. Для большинства окажется трудным сделать число ходов меньше 17.

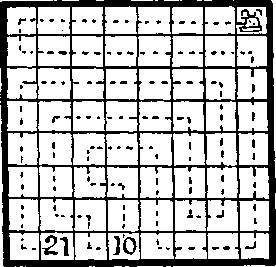
148. Путь показан на рисунке. Можно заметить, что десятый ход приводит нас в клетку, отмеченную числом 10, а последний, 21-й ход заканчивается в клетке 21.

149. Пунктирная линия показывает путь, состоящий из 22 прямолинейных отрезков, которым рыцарь добрался до девы. Необходимо, войдя в первую камеру, немедленно вернуться назад, прежде чем войти в другую камеру. Иначе вам не удастся найти решение.

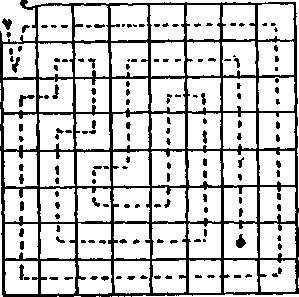
150. Если узник выберет путь, показанный на рисунке, где для простоты не изображены двери, то он посетит каждую камеру по одному разу, пройдя 57 прямо линейных участков. Ни при каком пути ладьи по шахматной доске нельзя превзойти это число.

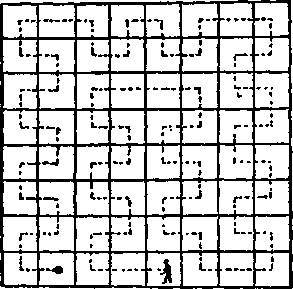
151. Прежде всего наименьшее число прямолинейных участков в каждом случае равно 22, и, дабы ни одну ячейку не посетить дважды, совершенно необходимо, чтобы каждый зашел в первую камеру, а затем немедленно «посетил» ту, из которой отправился; после этого он должен следовать вдоль пути, указанного на рисунке. Путь человека обозначен сплошной линией, а путь льва — пунктиром. Можно следовать вдоль каждого пути с двумя карандашами в руках и заметить, что человек и лев ни разу не встретились, хотя есть одно место, где они «мелькали в поле зрения друг друга». Далее мы обнаружим, что, двигаясь с постоянной скоростью, они никогда не окажутся в поле зрения друг друга. Однако на рисунке можно заметить, что лев и человек оказываются в камерах, обозначенных буквой А, одновременно и, следовательно, могут увидеть друг друга через открытые двери. То же происходит, когда они оказываются в камерах В, причем верхние буквы в обоих случаях показывают положение человека, а нижние — положение льва. В-первом случае лев устремляется прямо к человеку, тогда как человек, кажется, пытается зайти ко льву с тыла. Второй случай несколько более подозрителен, ибо похоже, что они здесь удирают друг от друга!

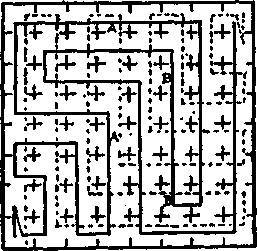
152. Я показал на рисунке, каким образом слон может посетить каждое из намеченных мест за 17 ходов. Очевидно, что мы должны начать с одного углового квадрата и закончить в диагонально противоположном. Головоломку нельзя решить за меньшее число ходов.

153. Передвигайте шашки следующим образом: 2—3, 9—4, 10—7, 3—8, 4-2, 7—5, 8—6, 5—10, 6—9, 2—5, 1—6, 6—4, 5—3, 10—8, 4—7, 3—2, 8—1, 7—10. Теперь белые шашки поменялись местами с красными за 18 ходов при соблюдении заданных условий.

154. Играйте следующим образом, используя обозначения, основанные на нумерации клеток на рисунке А.

На рисунке Б показано положение после девятого хода. Слоны на клетках 1 к 20 еще не ходили, но 2 и 19 уже двигались вперед, а затем вернулись назад. В конце 1 и 19, 2 и 20, 3 и 17, 4 и 18 поменяются местами. Обратите внимание на позицию после тринадцатого хода.

155. На приведенном рисунке показан второй вариант турне ферзя. Если вы прервете линию в точке J и уберете более короткий участок этой прямой, то получите искомый путь для любой клетки J. Если вы прервете линию в I, то получите невозвратное решение, начинающееся из любой клетки I. А если вы прервете линию в G, то получите решение для любой клетки G. Ранее приведенное турне ферзя можно также прервать в трех различных местах, однако я воспользовался возможностью привести второе турне.

156. Рисунок говорит сам за себя. Все звезды вычеркиваются за 14 прямолинейных движений, причем путь начинается и заканчивается белой звездой.

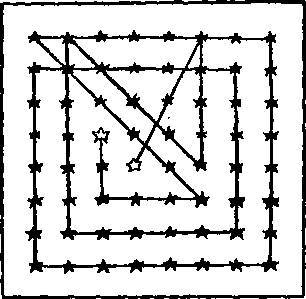
157. Решение вы видите на рисунке. Числа показывают направления прямых в их правильном порядке.

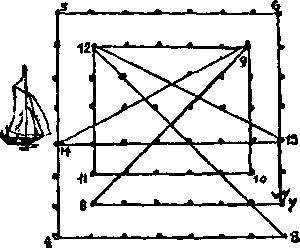
Можно заметить, что седьмой курс заканчивается у буя с флажком, как и требовалось.

158. В данном случае мы выходим за границы квадрата. Кроме того, все наши движения производятся ходом ферзя. Существуют 3 или 4 решения задачи.

Здесь приводится одно из них.

Можно заметить, что конькобежец вычеркивает все звездочки за один непрерывный путь, состоящий из 14 прямолинейных участков и возвращающийся в исходную точку. Чтобы проследить этот путь, нужно всегда двигаться по прямой как можно дальше до поворота.

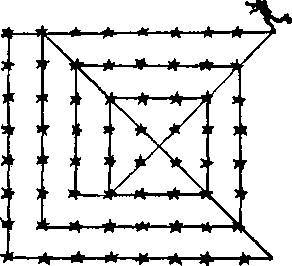
159. На рисунке показано, каким образом все звездочки можно вычеркнуть за 12 прямолинейных движений, начиная и заканчивая черной звездой.

160. Правильное решение головоломки показано на рисунке сплошной линией. За 5 ходов ферзь проходит наибольшее возможное для него при заданных условиях расстояние. Пунктирная линия на исходном рисунке показывает путь, который предлагает большинство читателей, однако он короче первого. Допустим, что расстояние между центрами соседних клеток, расположенных на одной горизонтали или вертикали, равно 2 дюймам и что ферзь движется из центра исходной клетки в центр той клетки, где он останавливается; тогда в первом случае путь превосходит 67,9 дюйма, а во втором — не превышает 67,8 дюйма. Разница не велика, но достаточна для того, чтобы выделить более длинный путь. Все другие пути короче.