Производная. Пусть требуется определить скорость прямолинейно движущейся материальной точки. Если движение равномерно, то пройденный точкой путь пропорционален времени движения; скорость такого движения можно определить как путь, пройденный за единицу времени, или как отношение пути, пройденного за некоторый промежуток времени, к длительности этого промежутка. Если же движение неравномерно, то пути, пройденные точкой в одинаковые по длительности промежутки времени, будут, вообще говоря, различными. Пример неравномерного движения даёт тело, свободно падающее в пустоте. Закон движения такого тела выражается формулой s = gt²/2, где s — пройденный путь с начала падения (в метрах), t — время падения (в секундах), g — постоянная величина, ускорение свободного падения, g » 9,81 м/сек². За первую секунду падения тело пройдёт около 4,9 м, за вторую — около 14,7 м, а за десятую — около 93,2 м, т. е. падение происходит неравномерно. Поэтому приведённое выше определение скорости здесь неприемлемо. В этом случае рассматривается средняя скорость движения за некоторый промежуток времени после (или до) фиксированного момента t; она определяется как отношение длины пути, пройденного за этот промежуток времени, к его длительности. Эта средняя скорость зависит не только от момента t, но и от выбора промежутка времени. В нашем примере средняя скорость падения за промежуток времени от t до t + Dt равна

 

Это выражение при неограниченном уменьшении промежутка времени Dt приближается к величине gt, которую называют скоростью движения в момент времени t. Таким образом, скорость движения в какой-либо момент времени определяется как предел средней скорости, когда промежуток времени неограниченно уменьшается.

  В общем случае эти вычисления надо проводить для любого момента времени t, промежутка времени от t до t + Dt и закона движения, выражаемого формулой s = f (t). Тогда средняя скорость движения за промежуток времени от t до t + Dt даётся формулой Ds/Dt, где Ds = f (t + Dt) — f (t), а скорость движения в момент времени t равна

 

Основное преимущество скорости в данный момент времени, или мгновенной скорости, перед средней скоростью состоит в том, что она, как и закон движения, является функцией времени t, а не функцией интервала (t, t + Dt). С другой стороны, мгновенная скорость представляет собой некоторую абстракцию, поскольку непосредственному измерению поддаётся средняя, а не мгновенная скорость.

  К выражению типа (*) приводит и задача (см. рис.) построения касательной к плоской кривой в некоторой её точке М. Пусть кривая Г есть график функции у = f (x). Положение касательной будет определено, если будет найден её угловой коэффициент, т. е. тангенс угла a, образованного касательной с осью Ox. Обозначим через x абсциссу точки М, а через x₁ = x + Dх — абсциссу точки M₁. Угловой коэффициент секущей MM₁ равен

 

где Dy = M₁N = f (x + Dx) — f (x) — приращение функции на отрезке [x, x₁]. Определяя касательную в точке М как предельное положение секущей MM₁, когда x₁ стремится к x, получаем

 

  Отвлекаясь от механического или геометрического содержания приведённых задач и выделяя общий для них приём решения, приходят к понятию производной. Производной функции у = f (x) в точке х называется предел (если он существует) отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, так что

 

С помощью производной определяется, кроме уже рассмотренных, ряд важных понятий естествознания. Например, сила тока определяется как предел

 

где Dq — положительный электрический заряд, переносимый через сечение цепи за время Dt; скорость химической реакции определяется как предел

 

где DQ — изменение количества вещества за время Dt; вообще, производная по времени есть мера скорости процесса, применимая к самым разнообразным физическим величинам.

  Производную функции y = f (x) обозначают f' (x), у', dy/dx, df/dx или Df (х). Если функция y = f (x) имеет в точке х производную, то она определена как в самой точке x, так и в некоторой окрестности этой точки и непрерывна в точке x. Обратное заключение было бы, однако, неверным. Например, непрерывная в каждой точке функция

 

графиком которой служат биссектрисы первого и второго координатных углов, при х = 0 не имеет производной, т.к. отношение Dу/Dх не имеет предела при Dx ® 0: если Dх > 0, это отношение равно +1, а если Dx < 0, то оно равно -1. Более того, существуют непрерывные функции, не имеющие производной ни в одной точке (см. Непрерывная функция).

  Операцию нахождения производной называют дифференцированием. На классе функций, имеющих производную, эта операция линейна.

  Таблица формул и правил дифференцирования

  (C)´ = 0; (xⁿ)´ = nx^n-1;

  (a^х)´ = a^x ln a и (e^x)´ = e^x;

  (log_ax)´ = 1/x ln a и (ln x)´ = 1/x;

  (sin x)´ = cos x; (cos x)´ = – sin x;

  (tg x)´ = 1/cos² x; (ctg x)´ = – 1/sin² x;

 

  (arc tg x)´ = 1/(1 + x²).

  [f (x) ± g (x)]´ = f ´(x) ± g´(x);

  [Cf (x)]´ = Cf ´(x);

  [f (x) g (x)]´ = f´´(x) g (x) + f (x) g ´(x);

 

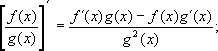
если y = f (u) и u = j(x), т. е. y = f [j(x)], то dy/dx = (dy/du)×(du/dx) = f¢ (u)j¢(x).

Здесь С, n и a — постоянные, a > 0. Эта таблица, в частности, показывает, что производная от всякой элементарной функции есть снова элементарная функция.

  Если производная f' (x), в свою очередь, имеет производную, то её называют второй производной функции у = f (x) и обозначают

  у", f" (x), d²y/dx², d²f/dx² или D²f (x).