Широким опросом я обнаружил, что никто не может установить взаимосвязь этих чисел и руководящий принцип, которому они подчинены. По моему глубокому убеждению, они не образуют систему! Они — хаос!

Само собой разумеется, что в качестве системы счисления нельзя использовать хаотический набор цифр и чисел, подобный тому, о котором сейчас шла речь. Система начинается тогда, когда они подчинены определенному порядку перехода от одного числа к другому, определенным законам действия над ними.

Так, мы знаем, что в десятичной системе за числом 9 следует число 10, за 499 следует 500, а за 7855 — 7856. Такой переход от числа к числу мы обычно совершаем не задумываясь. Однако сознательно или бессознательно мы при этом всегда руководствуемся следующими правилами:

1. Заменить последнюю цифру числа следующей цифрой, имеющейся в этой системе (например, в числе 7855 заменить последнюю 5 на 6).

2. Если последняя цифра числа является наибольшей в этой системе, то ее следует заменить на наименьшую, а затем сдвинуться на одну колонку влево и заменить стоящую здесь цифру на старшую.

3. Если в этой колонке стоит наибольшая цифра системы, то надо повторять действие, предусмотренное предыдущим правилом, до тех пор, пока не встретится колонка, допускающая замену стоящей в ней цифры на старшую.

Попробуем, например, применить эти правила для перехода от числа 499 к следующему числу. Последняя цифра этого числа 9 является наибольшей цифрой в десятичной системе счисления, и согласно правилу 2 ее следует заменить на нуль. Сдвинувшись затем на одну колонку влево, видим, что и здесь стоит цифра 9. Согласно правилу 3 ее также заменяем на нуль, а затем, передвинувшись в следующую колонку, заменяем 4 на 5. В результате от числа 499 мы перейдем к числу 500.

Вот теперь, располагая методом, позволяющим переходить от одного числа к другому, мы можем утверждать, что ведем счет чисел по определенной системе; в нашем случае по десятичной.

Согласно этой системе сначала накапливаются единицы вплоть до 9. Следующее число 10 образуется двумя цифрами, ранее использованными для счета единиц. Цифра 1, записанная во второй колонке слева, или, как говорят, во втором разряде, означает, что счет теперь ведется десятками. Переход в третий разряд соответствует счету сотен и т. д. Число 499 фактически представляет собой 4 · 10² + 9 · 10¹ + 9 · 10⁰ = 499.

Число 7856 в действительности есть 7 · 10³ + 8 · 10² + 5 · 10¹ + 6 · 10⁰ = 7856.

А число 4,99 равно 4 · 10⁰ + 9 · 10^–1 + 9 · 10^–2 = 4,99.

Таким образом, в десятичной системе счисления каждое число представляет собой сумму различных степеней числа 10, то есть числа, равного количеству различных символов этой системы.

Само собой разумеется, что не только десятичная, но и любая другая система счисления подчинена определенным правилам. Попытаемся изобрести еще одну систему (кстати, она уже давно служит людям). Для этого припишем отверстию в перфоленте или импульсу тока символ единицы; отсутствию отверстия или паузе — символ нуля. Теперь мы располагаем двумя символами 1 и 0. Оказывается, они могут составить основу новой системы счисления, которая будет называться двоичной. В ней любые числа записываются в виде той или иной комбинации всего лишь двух цифр — нуля и единицы. Однако правила перехода от одного числа к следующему в двоичной системе точно такие же, что и в десятичной.

Первые две цифры 0 и 1 в обеих системах одинаковы, однако уже для числа 2 в двоичной системе отдельного символа нет. Эквивалентная ему цифра образуется использованием уже имеющихся двух цифр и записывается так: 10. Чтобы избежать путаницы, будем число 2 читать: один-ноль.

Следующее число получим, пользуясь приведенными выше правилами. Согласно первому из них оно запишется как 11.

Для записи следующего числа нам придется применить правило 3 и использовать запись уже в трех разрядах: получим — 100. Следующими числами в двоичной системе будут 101, 110, 111; затем будут следовать четырехразрядные числа 1000, 1001, 1010 и т. д. В таблице приведены эти числа вместе с соответствующими им десятичными числами.

Как в десятичной системе любое число представляет собой сумму различных степеней числа 10, так в двоичной системе любое число представляет собой сумму различных степеней числа 2.

Таким образом, десятичное число, эквивалентное числу 1101, записанному в двоичной системе, будет равно:

1101 = 1 · 2³ + 1 · 2² + 0 · 2¹ + 1 · 2⁰ = 1 · 8 + 1 · 4 + 0 · 2 + 1 · 1=8 + 4 + 1 = 13.

Ниже приведены числа, представляющие различные степени двойки; с их помощью легко отыскиваются десятичные эквиваленты двоичных чисел:

2⁰ = 1

2¹ = 2

2² = 4

2³ = 8

2⁴ = 16

2⁵ = 32

2⁶ = 64

2⁷ = 128

2⁸ = 256

2⁹ = 512

2¹⁰ = 1024

2¹¹ = 2048

2¹² = 4096

2¹³ = 8192

Но, конечно, чтобы перейти от двоичного числа к десятичному, совершенно не обязательно пользоваться таблицами. Для этой цели можно, например, воспользоваться способом, основанным на применении двух следующих правил, относящихся ко всем разрядам двоичного числа.

Начиная со старшего разряда следует поступать так:

1. Если в следующем разряде стоит нуль, удвойте то, что вы накопили.

2. Если в следующем разряде стоит единица, удвойте то, что вы накопили, и прибавьте еще единицу.

Давайте для примера найдем десятичный эквивалент двоичного числа 1101, строго выполняя указанные правила.

Начнем со старшего разряда. Удвоим единицу и согласно правилу 2 прибавим еще единицу. В результате получим 3. Затем переходим к следующему разряду. Теперь согласно правилу 1 получим 6. А затем удваиваем это число и прибавляем еще единицу. Как и следовало ожидать, получим число 13.

Так же несложно совершается переход от записи чисел в десятичной системе к записи их в двоичной системе. Для этого десятичное число следует разделить на два, частное вновь разделить на два и продолжить деление до тех пор, пока частное будет равно единице. Эта единица и остатки всех предыдущих делений образуют двоичное число, эквивалентное исходному десятичному. Запишем в качестве примера число 19 в двоичной системе. Для этого составим таблицу последовательных делений.

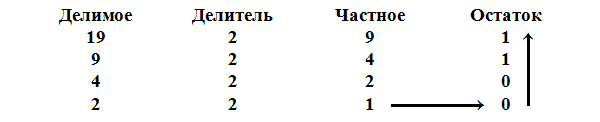
Выписав последнее частное и все остатки начиная снизу, найдем, что в двоичной системе 19 запишется так: 10011.

Вы, наверно, уже обратили внимание на то, что любое двоичное число, кроме нуля и единицы, требует при своей записи большего количества разрядов, чем эквивалентное ему десятичное число. Однако этот недостаток двоичной системы с избытком перекрывается простотой способов автоматической записи, чтения и передачи двоичных чисел, а также простотой автоматизации арифметических операций над ними.

При сложении десятичных чисел следует помнить, что 9 плюс 8 равно 17, 5 плюс 6 равно 11 и т. д. и т. д. а при их умножении следует помнить большую таблицу умножения. При сложении двоичных чисел достаточно запомнить три следующих простейших правила:

1) 0 плюс 0 равно 0.

2) 0 плюс 1 равно 1.