Если остановиться в наших рассуждениях на сказанном, то может возникнуть желание истолковать происхождение иллюзий искажения таким же образом, как толкуется изменение видимого размера при изменении видимого расстояния. Подобный эффект мы наблюдали при перцептивном перевертывании куба; к тому же нам известен закон Эммерта, выведенный при наблюдении зависимости размеров послеобраза от расстояния до экрана, на фоне которого этот образ виден. Однако такое истолкование не годится, потому что при иллюзиях искажения фигура все время воспринимается в плоскости. Правда, в ней всегда выражены перспективные элементы, но, вне всякого сомнения, нет необходимости воспринимать фигуры Понзо, Мюллера-Лайера и другие в трех измерениях, чтобы восприятие этих фигур содержало иллюзию искажения. Мы видим их на плоскости бумажного листа - и все же иллюзия налицо, а это совсем не то же самое, что было с перевертывающимся кубом. Куб и подобные ему фигуры меняют видимую форму только в тех случаях, когда они воспринимаются как трехмерные фигуры, но не тогда, когда они видны как плоские фигуры.
Поэтому проблему нельзя считать решенной. Быть может, эти искажения окажутся в конце концов никак не связанными со шкалированием размера и расстояния? А может быть, связь существует, но она хорошо замаскирована? Тот факт, что искажения соответствуют перспективным особенностям фигур, показывает, что второе предположение ближе к истине. Тогда в чем же заключается эта скрытая связь?
Зададим себе сначала такой вопрос: почему эти фигуры, явно содержащие перспективу, не воспринимаются как трехмерные? Ответ, по-видимому, ясен. Указания на глубину нейтрализуются фактурой фона. Доказать это нетрудно. Покройте рисунок светящейся краской, погасите свет - и вы устраните фон. Рисунок в таких условиях в большинстве случаев воспринимается как трехмерная фигура в соответствии с содержащимися в нем элементами перспективы.
Можно сделать больше: объективно измерить кажущуюся глубину таких фигур. Тогда мы свяжем величину "глубинности" со степенью искажения фигуры, наблюдаемой в плоскости.
Измерение кажущейся трехмерности картин
Неподготовленному человеку может показаться, что измерить кажущуюся глубину совершенно невозможно - ведь это задача, абсолютно непохожая на измерение положения предметов во внешнем пространстве. Как можно зафиксировать "внутреннее", воспринимаемое наблюдателем, пространство?
На первый взгляд кажется, что довольно точные результаты мы получим, попросту регистрируя движение наблюдателя, который касается предметов, расположенных на разных расстояниях от него (такой опыт можно поставить даже с тренированными животными). Пример: набрасывание колец на колышки, удаленные на разные расстояния. Но подобные эксперименты далеки от совершенства: регистрируемые ошибки в оценке расстояний содержат не только перцептивные погрешности, но и двигательные несовершенства, а мы не знаем, как велика доля первых. Задача отделения ошибок восприятия от ошибок исполнения - одна из самых трудных проблем исследования поведения.
Мы сумеем найти лучший способ измерения кажущейся глубины, если используем бинокулярное наблюдение как дальномер-эталон и его показания будем сравнивать с оценками глубины, найденными при наблюдении одним глазом.
Для этого прежде всего необходимо устранить всю стереоскопическую информацию, чтобы узнать величину монокулярного эффекта перспективы при наблюдении плоской фигуры. Затем надо нейтрализовать влияние фона, видимая фактура которого может противоречить перспективе, заключенной в рисунке, отчего возникает перцептивный парадокс. Чтобы выполнить первое условие, достаточно вести наблюдение одним глазом. Выполнение второго условия достигается, если покрыть рисунок светящейся краской и погрузить комнату в темноту. Того же эффекта можно добиться и другим способом: изготовить диапозитив (точнее, "дианегатив" - прозрачный рисунок на непрозрачном фоне) и осветить его на просвет слабым равномерным светом (идеальный вариант - электро люминесцентная панель, помещенная непосредственно за "дианегативом"). Теперь осталось найти способ ввести какой-нибудь указатель в пределы фигуры; этот указатель должен восприниматься обоими глазами, и его следует сделать движущимся в глубину, даже сквозь плоскость рисунка. Это достигается оптическими методами.
Указатель представляет собой маленькое пятно света, отраженное от полупрозрачного зеркала, которое повернуто под углом 45 градусов к линии взора, направленного на рисунок; рисунок рассматривают прямо сквозь полупрозрачное зеркало. Световое пятнышко видно там же, где находится рисунок, - оптически оно именно там и находится. Если длина светового луча от глаз к указателю оказывается больше, чем от глаз до рисунка, то указатель виден позади, дальше рисунка; если первая меньше второй, то указатель виден ближе, перед рисунком. Осталось сделать так, чтобы рисунок (вернее, фигура) был виден лишь одному глазу, а указатель - обоим. Тогда мы сможем использовать бинокулярное зрение как дальномер для определения удаленности любой части фигуры, воспринимаемой одним глазом; это позволит нам промерить воспринимаемые одним глазом расстояния до всех частей фигуры и составить таким образом карту зрительного пространства. Цель достигается, если установить поляризаторы света перед картиной и перед одним глазом (крест-накрест): перед диапозитивом помещаем лист "поляроида", ориентируя плоскость поляризации под углом 45 градусов к горизонтали, перед глазом помещаем такой же фильтр, но ориентированный под углом 135 градусов к горизонтали; этот глаз картины видеть не будет. Поскольку указатель освещен неполяризованным светом, оба глаза видят указатель, но лишь один из них - фигуру, содержащую искажение. Измерение зрительного пространства производят, перемещая световой указатель поочередно к разным частям фигуры и затем (оптически) приближая или удаляя его до тех пор, пока он не будет воспринят - стереоскопически - на том же расстоянии, что и данный (монокулярно видимый) элемент фигуры.
Кстати, не обязательно пользоваться одним указателем; их можно сделать несколько и разместить у разных точек фигуры, чтобы измерить удаленность всех частей фигуры одновременно. Этот глубиномерный аппарат мы назвали "ящиком Пандоры" (рис. 73).
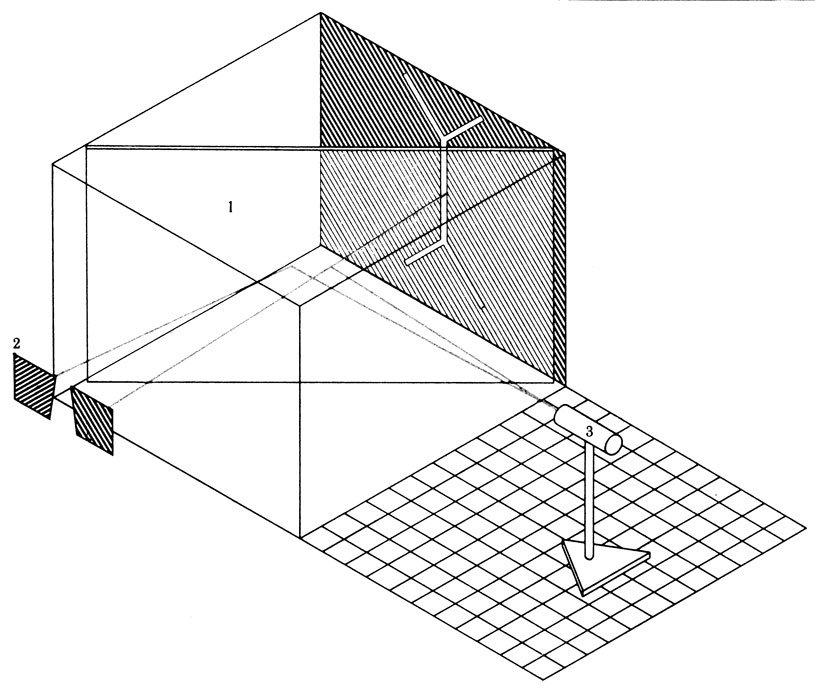
Рис. 73. 'Ящик Пандоры' - аппарат для измерения кажущейся глубины картин. 1 - полупрозрачное зеркало; 2 - поляроидные очки; 3 - проектор светового индикатора
Что получится, когда мы измерим кажущуюся глубину на картинах, содержащих иллюзию? Устранив противоречивую информацию, которая поступает от стереозрения и от фактуры фона, мы получим доказательство того, что фигуры, содержащие иллюзии искажения, - фигуры Понзо (железнодорожный путь), Мюллера-Лайера (стрелы) и им подобные - действительно воспринимаются в трех измерениях и поддаются промерам также в трех измерениях. Меняя степень выраженности перспективных элементов в этих фигурах, мы находим связь между кажущейся глубиной фигур и величиной их перцептивного искажения. На графике (рис. 74) видна эта экспериментально найденная зависимость: увеличение перспективности фигуры приводит к увеличению перцептивного искажения.
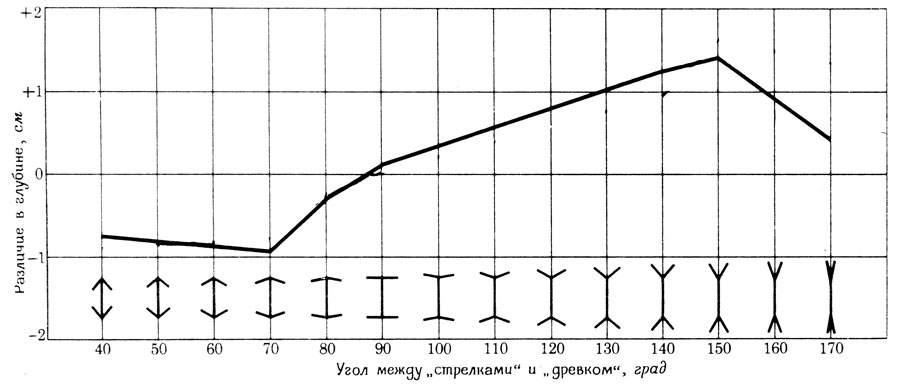
Рис. 74. Зависимость величины иллюзорного искажения глубины (измеренного с помощью 'ящика Пандоры') от положения штрихов, ограничивающих отрезки в фигуре Мюллера-Лайера
Результаты этих экспериментов позволяют предположить, что перспектива влияет на зрительное шкалиро-вание прямо - даже в тех случаях, когда указаниям перспективы противоречат другие факторы (например, видимая фактура фона), противодействующие непосредственному восприятию глубины. Мы считаем так потому, что иллюзии искажения воспринимаются даже на фоне, имеющем явно видимую фактуру (как, например, на страницах этой книги), - фигуры выглядят при этом плоскими, но искаженными.