Просто? Но можно сделать ещё проще, прибегнув к логическому выражению.

Логические выражения

Данные логического типа можно получать в результате не совсем обычных вычислений. В этих вычислениях порой не увидишь ни чисел, ни арифметических действий, – речь идет о логических выражениях. Например, сравнивая две строки, вы задаетесь вопросом, равны ли они? Ответом может быть либо «да», либо «нет», или, выражаясь на языке Паскаль, TRUE или FALSE. Следовательно, сравнение строк, которое мы применяли в условных и циклических операторах, – это логическое выражение. А раз так, то результат сравнения можно присвоить булевой переменной. В приведенном выше примере вместо условного оператора можно записать выражение:

      B := S=’1’;       { равносильно if S=’1’ then B:= true else B:= false }

Здесь справа от знака присваивания стоит логическое выражение S=’1’, и в переменную B попадет TRUE, если S будет содержать строку «1» и FALSE – в любом другом случае.

Булевы переменные и выражения применяют везде, где требуется проверка условия, например, в условном и циклическом операторах:

if B

      then... { выполняется, если B=true }

      else... { выполняется, если B=false }

repeat

      { цикл выполняется, пока B=false }

until B

Замечу здесь, что «if B then…» равносильно «if B=TRUE then…».

К чему ещё годны булевы данные? С ними производят логические операции, но к операциям обратимся чуть позже, – пора вернуться к нашей автомобильной задаче.

С высоты птичьего полета

Напомню, что мы работаем над программой для навигатора автомобиля, принимающего сигналы от спутников системы ГЛОНАСС. Из космоса прекрасно видны все улицы и пробки города. Пусть все возможные маршруты от дома до школы известны заранее, а спутник сообщает лишь о том, открыта ли для движения та или иная улица. Если улица открыта, спутник сообщает об этом значением TRUE, а иначе – значением FALSE. Увы, к настоящему спутнику мы пока не подключены, и вводить данные о пробках придется вручную. Результатом работы нашей программы будет сообщение о том, можно ли проехать в школу (TRUE), или нет (FALSE).

Вот первый маршрут. Предположим, путь от дома до школы пролегает по двум улицам так, как показано на рис. 31.

Рис.31 – – Схема первого маршрута

Очевидно, что отразить состояние двух улиц можно двумя булевыми переменными, назовем их A и B. Объявим переменные и введем данные в них.

var A, B : Boolean; S: string;

begin

      Write(’Улица A открыта? ’); Readln(S); A:= S=’1’;

      Write(’Улица B открыта? ’); Readln(S); B:= S=’1’;

Здесь, как мы условились раньше, значение TRUE вводится цифрой «1».

Обратите внимание на новую для вас процедуру Write, – это «младшая сестра» процедуры Writeln. В отличие от «старшей сестры», после вывода сообщения она не переводит курсор на следующую строчку, – это удобно при запросе данных.

Ну-с, данные со спутника введены, и можно заняться их обработкой. Ясно, что для проезда в школу обе улицы должны быть открыты. Условными операторами это нехитрое рассуждение можно выразить так:

      S:=’Топай пешком’;

      if A then

      if B then S:=’Поезжай на машине!’;

Исходное значение – «Топай пешком» – заносим в переменную S заранее. Оно изменится тогда, когда обе булевы переменные станут равны TRUE. Согласитесь, это решение из двух условных операторов оказалось несложным. Но до поры до времени. Что, если маршрутов станет много, и каждый будет пролегать через несколько улиц? Программа превратится в нагромождение условных операторов, больше похожее на хаос землетрясения! Страшно? Тогда рассмотрим другой подход. Суть его в том, чтобы выразить решение на обычном человеческом языке, а затем превратить это высказывание в логическое выражение.

Решение нашей задачи можно высказать так: «проехать можно, если открыта улица A И открыта улица B». Обратите внимание на выделенный курсивом союз «И». Чтобы превратить это рассуждение в логическое выражение и записать на Паскале, надо лишь перевести союз «И» на английский язык – это будет «AND», а названия улиц заменить логическими переменными A и B. И вот результат такого перевода.

      if A and B

      then S:=’Поезжай на машине!’

      else S:=’Топай пешком!’;

Вместо двух условных операторов остался один. Готовая программа будет такой.

{ P_13_1 – первый маршрут проезда }

var A, B : Boolean; S: string;

begin

      { ввод данных со «спутника» }

      Write(’Улица A:’); Readln(S); A:= S=’1’;

      Write(’Улица B:’); Readln(S); B:= S=’1’;

      { решение }

      if A and B

      then S:=’Поезжай на машине!’

      else S:=’Топай пешком!’;

      Writeln(S); Readln

end.

Испытайте программу при разных сочетаниях входных данных и проверьте, не врёт ли она?

Теперь рассмотрим другой маршрут, здесь попасть в школу можно по любой из двух улиц (рис. 32).

Рис.32 – Схема проезда, второй вариант

Обычным языком молвим так: «проезд возможен, если открыта улица A ИЛИ открыта улица B». Союз «ИЛИ» тоже припасен в Паскале, по-английски он пишется «OR». В этом случае решение будет таким.

      if A or B

      then S:=’Поезжай на машине!’

      else S:=’Топай пешком!’;

А вот маршрут на рис. 33 более замысловат.

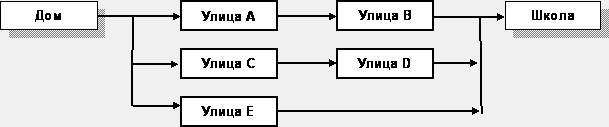
Рис.33 – Схема проезда, третий вариант

Слабо ли вам выразить решение для этого случая? Сказать на обычном языке легко: «проехать можно, если открыта A И открыта B ИЛИ открыта C И открыта D ИЛИ открыта E». Слово «улица» я пропустил. Все, решение готово! Осталось лишь перевести его на язык Паскаль.

      if A and B or C and D or E

      then S:=’Поезжай на машине!’

      else S:=’Топай пешком!’;

Как просто! Здесь опять выделено курсивом логическое выражение. Только теперь оно составлено из булевых переменных и булевых операций AND (И) и OR (ИЛИ). Иногда эти операции называют логическим умножением и логическим сложением. Сходство с арифметикой здесь в том, что каждая логическая операция обладает в выражении своим старшинством: умножение AND выполняется раньше сложения OR. Когда эту последовательность надо изменить, применяют скобки. Пример такого рода показан на рис. 34 (перекресток).

Рис.34 – Схема проезда, четвертый вариант

Сначала скажем словами: «проехать можно, если открыта A ИЛИ открыта B И открыта C ИЛИ открыта D». Переведя на Паскаль буквально, без скобок, получим: