N := 10 div 3; { =3 } M := 10 mod 3; { =1 }
N := 10 div 4; { =2 } M := 10 mod 4; { =2 }
N := 10 div 5; { =2 } M := 10 mod 5; { =0 }
N := 10 div 6; { =1 } M := 10 mod 6; { =4 }
Как видите, операции с целыми числами дают целый результат даже при делении, поскольку дробная часть отбрасывается.
Числовые переменные и выражения можно сравнивать между собой на равенство (=), неравенство (<>), больше (>), меньше (<), больше или равно (>=), меньше или равно (<=). При сравнении получается, как всегда, булев результат, например:
var X, Y: integer;
B: Boolean;
begin
X:=5; Y:=10;
B:= X=Y; { B = FALSE }
B:= X<Y; { B = TRUE }
B:= X=Y-5; { B = TRUE }
end.
А как быть с вводом и выводом числовых данных, нет ли тут сложностей? К счастью, нет. Так же как и строки, числовые данные вводятся процедурой Readln, а печатаются процедурами Write и Writeln, например:
Readln(X);
Writeln(X);
Writeln(’Y=’, X+10);
В последнем операторе на экран выводится строковая константа ’Y=’ и результат сложения X+10.
Теперь вы снабжены всем необходимым для написания экзаменатора.
Алгоритм экзаменатора
Прежде всего, уточним алгоритм создаваемой программы. Живой экзаменатор сам придумывает примеры для умножения. Но нам это пока не под силу – маловато знаний – отложим этот вариант до следующей главы. А пока экзаменуемый будет сам «создавать себе проблемы», то есть будет вводить сомножители по запросу программы вручную. Пример диалога может выглядеть, например, так:
Первый сомножитель A = 7
Второй сомножитель B = 7
Произведение A*B = 47
Ошибка, повтори таблицу умножения!
И так далее. Здесь выделенные курсивом числа 7, 7 и 47 пользователь ввел сам. Разумеется, что задания надо решать многократно, в цикле. Для выхода из цикла нужен какой-то признак, сигнал. Пусть таким сигналом будет ввод нуля в качестве ответа. Тогда блок-схема программы получается такой (рис. 37).
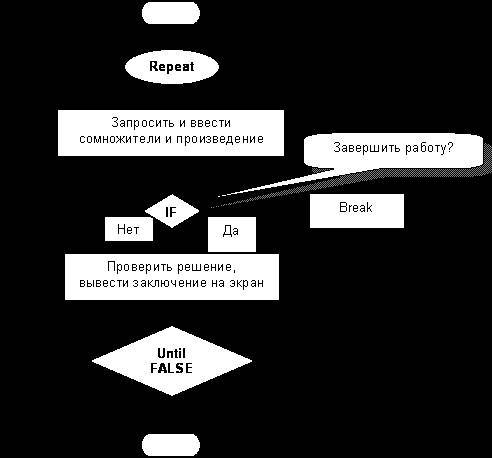
Рис.37 – Блок-схема программы проверки таблицы умножения
Обратите внимание на условие в операторе цикла REPEAT-UNTIL, – оно равно FALSE. Такой цикл будет продолжаться бесконечно, и выйти из него можно лишь процедурой BREAK, как показано на блок-схеме.
Экзаменатор, первый вариант
Вот теперь все готово для написания следующей программы.
{ P_14_1 – экзаменатор таблицы умножения, первый вариант }
var A, B, C : integer; { сомножители и произведение }
R: Boolean; { результат сравнения }
S: string; { сообщение для вывода на экран }
begin
repeat
{ ввод сомножителей и произведения }
Write(’Первый сомножитель A = ’); Readln(A);
Write(’Второй сомножитель B = ’); Readln(B);
Write(’Произведение A*B = ’); Readln(C);
if C=0 then break; { завершение цикла, если C=0 }
{ проверяем правильность вычисления }
R:= A*B=C; { R=true, если верно }
if R
then S:= ’Молодец, правильно!’
else S:= ’Ошибка, повтори таблицу умножения!’;
Writeln(S);
until false; { бесконечный цикл }
end.
Запустите программу и проверьте её работу. В следующий раз мы научим её придумывать сомножители, – так будет честнее. А пока подведем итоги.
Итоги
• Для вычислений в Паскале предусмотрены данные числового типа (INTEGER).
• К данным целого типа могут применяться четыре арифметических операции, а также операция нахождения остатка от деления.
• В результате сравнения численных данных получается булев результат, который может быть применен везде, где проверяется условие.
• Числовые данные вводятся оператором Readln и выводятся операторами Write и Writeln;
• Числовым переменным нельзя присваивать строковые значения и наоборот: строковым переменным нельзя присваивать числовые значения.
А слабо?
А) Найдите ошибки в следующей программе и объясните их.
var N, M : integer;
S : string;
begin
N:= ’10’;
S:= N + 5;
M:= S – 1;
if S=N then;
end.
Проверьте свои догадки, призвав на помощь компилятор.
Б) Перепишите программу «P_14_1», не прибегая к процедуре Break. В чем, по-вашему, слабость этого второго варианта? Можно ли обойтись в программе «P_14_1» без булевой переменной R и строковой S? Напишите такой вариант программы. Или слабо?
В) Пусть программа запросит три числа: A, B и C, а затем напечатает большее из них. Подсказка: примените булевы выражения вкупе с операциями сравнения, которые в булевых выражениях надо заключать в скобки, например:
if (A>=B) and (A>=C) then...
Примечание. Скобки ставят по той причине, что булевы операции можно выполнять и с числами, и такие операции приоритетней операций сравнения. О применении логических операций к числам сказано в главе 48.
Г) В стене прорублено прямоугольное сквозное отверстие со сторонами A и B. Пусть ваши программы разберутся, пройдет ли в него кирпич с ребрами X, Y, Z. Сделайте две программы для таких случаев:
• Известно, что A<B и X<Y<Z.
• Соотношение между сторонами неизвестно, и программе самой надо выяснить высоту и ширину, как отверстия, так и кирпича.
Д) Площадь земельного участка вычисляется умножением его сторон A и B. В программу вводятся стороны двух участков (A1, B1 и A2, B2), пусть она напечатает ширину и длину того участка, что больше по площади. Ширина должна быть не больше длины.
Глава 15
Айда в Монте-Карло!

Монте-Карло – весёлый пригород в княжестве Монако, славный своими игорными заведениями. Там, по словам Поэта, жертвуют необходимым в надежде приобрести излишнее. Но к чему нам игорный бизнес, – спросите, – когда мы заняты программой-экзаменатором? Не забывайте, однако, что наш первоклашка пока ещё сам придумывает себе примеры, а это неразумно. Избавим его от ввода сомножителей, – пусть программа сама «изобретает» их. Потому и обращаемся к азартным играм.
Куда ни глянь – то процедура, то функция!
Современные программы очень сложны. И, как любое крупное изделие, заключают в себе труд десятков и сотен специалистов. Трудно поверить, но большинство программистов, работающих над крупным проектом, не видят его в целом, что не мешает им выполнять свою часть работы. Как такое возможно?
Чтобы понять это, оглянитесь вокруг. Обойдутся ли жители города или страны друг без друга? Кем бы ты ни был – врачом, водителем или сапожником – не проживешь без услуг иных граждан, – все мы зависим друг от друга! Но спросите, к примеру, сталевара, куда пойдет выплавляемая им сталь? Он только плечами пожмет!