— Прямо ответить на этот вопрос невозможно, — сказал Коникос, — но уж раз мы знаем, что такие весьма точные вычисления существовали, мы убеждаемся в том, что либо это делалось просто из научной любознательности, либо это были упражнения для учеников. Но и в том и другом случае это все-таки очень похоже на то, что мы теперь называем наукой. Возможно, что некоторые вопросы, вроде теории квадратного уравнения, изучались преимущественно на числовых решениях. Может быть, это не самый лучший способ анализа, но и он давал некоторые результаты. Квадратное уравнение вавилоняне решали просто: находили два числа по их сумме и произведению… Что ты на это скажешь?

— На основании формул Виета как раз выходит квадратное уравнение:

х² + рх + q = 0.

Сумма его корней равна р с обратным знаком, а их произведение = q.

— Вавилонянин решал задачу так: либо эти искомые величины (корни) равны между собой, либо нет. Если нет, то между ними есть некая разность z. Тогда можно написать, что

x₁ = -p/2 + z; x₂ = — p/2 — z, где z = 1/2(x₁ — x₂).

— 306 —

Затем во второе уравнение x₁ · x₂ = q подставляем эти значения корней и приходим к известной формуле квадратного уравнения, что нетрудно проверить.

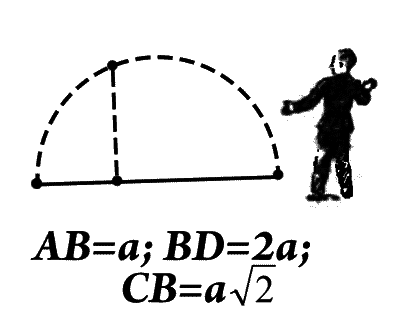
AB = a; BD = 2a; CB = a√2

Илюша немного повозился с расчетами, выяснил, что получается, а затем сказал:

— Но ведь ученый халдеи не знал формул Виета?

— Формул, конечно, он не знал, но самый факт определенных взаимоотношений между исходными данными такой задачи и ее решением не мог быть для него тайной, потому что тогда он не сумел бы так решить задачу. Формулировать это еще не умели и не понимали, может быть, сколь это полезно, но факт был известен. Догадываешься, в чем тут разница?

— Как будто… то есть, как вы говорите, не знали, почему?

— Вот именно, — подтвердил Радикс. — Удвоить квадрат оказалось довольно просто, а основное правило решения выясняется при помощи теоремы Пифагора. Если сторона квадрата равна а, то мы узнаем х из пропорции:

Ты, наверно, помнишь, как геометрически производится построение средней пропорциональной?

— Конечно! — отвечал мальчик. — Это мы по геометрии проходили. Откладываешь на прямой отрезки, равные а и 2а, и на их сумме, то есть на 3а, строишь полуокружность, радиус которой равен 1,5а. А теперь, если АВ будет отрезок а и 2а отрезок BD, то из точки В ты восстанавливаешь перпендикуляр до пересечения с окружностью — это и будет искомая средняя пропорциональная. Доказать, что это так, нетрудно. Теорема Пифагора все тут объясняет.

— Хорошо. Таким образом, тебе, следовательно, ясно, что, применяя это несложное построение, для которого ты пользуешься двумя известными тебе по своим свойствам геометрическими местами, то есть прямой и окружностью — иначе сказать, линейкой и циркулем, — ты получишь совершенно точно искомую величину. Но затем стал вопрос об удвоении объема. Тут нужен не квадратный, а кубический корень из двух. Конечно, и для него не так уж трудно найти грубое приближение, вроде дроби 29/23, потому что, если эту дробь возвести в куб, получится 24389/12167 что равно 2,0045, то есть двойка с ошибкой

— 307 —

 меньше пяти тысячных. Опять для целей строительства — прекрасное приближение! Но и в этом вопросе, который оброс в Древней Греции разными легендами и широко обсуждался, древнегреческий ученый действует по-особому. И для куба Гиппократ Хиосский вводит в пропорцию еще одну величину, у, причем он допускает, что между х и у соблюдается то же соотношение, что и между а и х. Строится пропорция

а : х = х : у = у : b,

откуда

x² = ay; y² = xb; x⁴ = a²y² = a²xb;

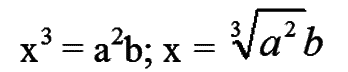
Положив теперь b = 2а, мы и получаем искомое решение:

х³ = 2а³; 

— А тут я чего-то, наверно, не понимаю, — признался Илья. — Зачем же Гиппократу понадобились все эти сложности[24] с его пропорцией? Ведь то, что ты называешь решением, то есть равенство х³ = 2а³, можно прямо написать из условий задачи. Для чего здесь нужна была эта длинная пропорция?

— Видишь ли, чтобы сообразить, зачем Гиппократу понадобилась эта сложная пропорция, надо вспомнить, что греки не располагали современной символикой. Это ты теперь можешь написать сразу:

а у греков пропорция была единственным способом для построения кратных соотношений между величинами. Следы этого громоздкого пропорционального подхода к подобным вопросам можно заметить вплоть до семнадцатого века вашей эры. Гиппократ придумал нужную пропорцию, и заслуга его в том, что он формулировал решение задачи, то есть он «составил уравнение», которое должен был далее решить геометрически, построением. Но Гиппократу это все-таки не удалось. Он только указал общий принцип решения. Решили эту задачу другие греческие математики, в том числе Менехм, ученый, который много занимался коническими сечениями (так что три эти сечения даже назывались в его честь «триа—

— 308 —

дой Менехма»). Это решение представляет собой нечто более сложное, нежели известное тебе построение средней пропорциональной. Искомый отрезок х строится при помощи двух пересекающихся парабол, поскольку парабола имеет близкое отношение к средним пропорциональным.

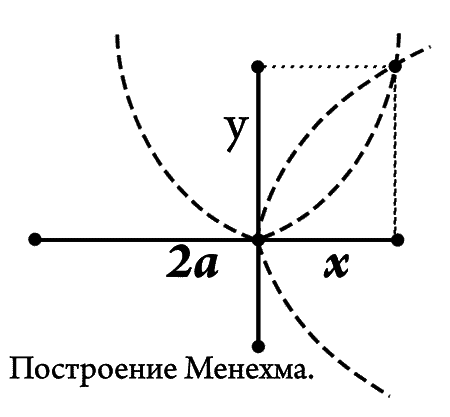
Параболы:

х² = аy; y² = аx;

Ищется средняя пропорциональная между a и 2a.

Впрочем, другие математики древности дали иные решения, не менее остроумные, и подошли впервые к решению кубического уравнения. Рассказ об этой задаче очень популярен среди ученых Возрождения, и для нас интереснее всего то, что принцип Гиппократа и всех, кто шел по его пути, представляет собой не только решение одной-единственной задачи, а является решением определенного типа задач на две средние пропорциональные. Этот вывод уже греческий.

— Это справедливо, — заметил Асимптотос, — но вот что еще можно отметить. Греческая разработка древневосточной науки привела постепенно греков к убеждению, что геометрия покоится на некоторых общих положениях, из которых путем ясного, простого и последовательного рассуждения можно вывести все важнейшие теоремы. Самые размышления стали глубже и проще: вместо того, чтобы покоряться неведомым силам природы, человек стал доискиваться их причин и мало-помалу пришел к заключению, что мировой порядок может быть изложен при помощи вычислений, то есть математически.

Разумеется, успехи вавилонских вычислителей-астрономов очень помогли этому. В Греции возникла пифагорейская школа мыслителей, которая учила, что все на свете определяется числом, причем целым. Значение этой школы в том, что она утверждала; мировой порядок есть нечто от человека не зависящее, что законы природы представляют собой не просто что-то таинственное, но нечто сложное, однако постижимое для человека. И вот при разработке этого учения древние мыслители столкнулись с явлением, которого не знал Древний Восток, — с иррациональностью, которая никакими числами точно выражена быть не может. Это открытие разрушило веру в целое число, а с другой стороны, показало, что геометрия в некотором смысле сильнее арифметики, ибо построить корень из двух нетрудно, а вычислить невозможно.