Помня эти эйлеровы правила, вы сумеете без труда решать головоломки, связанные с вычерчиванием кривых и обходом хитроумных маршрутов. Однако такие задачи, если осложнить их одним или двумя дополнительными условиями, нередко превращаются в труднейшие проблемы. Рассмотрим, например, сеть, изображенную на рис. 121.

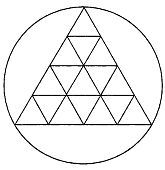
Рис. 121 Как обойти все линии, совершив минимальное число поворотов?

Все ее узлы четны. Как мы уже знаем, такую сеть можно начертить, не отрывая пера от бумаги и не проходя ни по одному ее участку дважды. Усложним теперь задачу: разрешим проходить любой участок сети неограниченное число раз, а начинать и заканчивать обход сети в любых двух ее точках. Спрашивается, чему равно наименьшее число поворотов, которое необходимо совершить, чтобы побывать на всех без исключения участках сети?

Маршрут предполагается непрерывным, без прыжков; остановка и возвращение назад по одной и той же прямой считается поворотом.

В основе механических головоломок с веревочками и колечками нередко лежит топологическая теория узлов. Одна из лучших головоломок этого типа изображена на рис. 122.

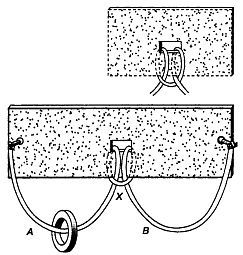
Рис. 122 Можно ли, не развязывая веревки, передвинуть кольцо в петлю В?

Ее нетрудно сделать самому из куска плотного картона, веревочки и колечка таких размеров, чтобы оно не проходило через центральное отверстие. Чем больше кусок картона и чем тяжелее веревочка, тем легче производить соответствующие манипуляции. Задача заключается в том, чтобы переместить кольцо из петли А в петлю В, не разрезая веревочки и не отвязывая ее концов.

Эту головоломку можно найти во многих старых сборниках занимательных задач, но обычно ее формулируют в крайне упрощенной форме: концы веревочки не привязывают, как это сделано у нас, к краям картона, а, пропустив через маленькие дырочки, прикрепляют к пуговицам, не позволяющим веревочке выскользнуть. В этом варианте задача имеет весьма неизящное решение: петлю X по очереди продевают в дырочки у краев картона и накидывают на пуговицы. Существует более хитроумное решение, в котором концы веревочки вообще никак не используются. Интересно заметить, что если один конец веревочки проходит под петлей X, а другой — над X (так, как показано на рис. 122 вверху), то задача не имеет решения.

Среди многих математических игр, имеющих любопытные топологические особенности, нельзя не назвать восточную игру го и широко распространенную детскую игру в точки и квадраты.

В последнюю играют так. На листке клетчатой бумаги точками отмечают вершины всех клеточек, образующих какой-нибудь прямоугольник. Играющие по очереди соединяют отрезками прямых любые две соседние точки. Если получающаяся ломаная во время очередного хода замыкается, образуя квадрат, то играющий ставит внутри него свою метку и ходит снова. После того как все линии проведены, победителем объявляется тот, кто сумел построить наибольшее число квадратов. Если игроки достаточно искусны, то игра в точки и квадраты при всей своей простоте может быть увлекательной, ибо, жертвуя квадратами в гамбите, игроки получают возможность с лихвой вознаградить себя построением большего числа квадратов в эндшпиле.

Хотя игра в точки и квадраты распространена ничуть не меньше, чем игра в крестики и нолики, подробный математический анализ ее до сих пор не был опубликован. Даже в том случае, когда «оперативным простором» служит квадрат размером 4x4 (из шестнадцати точек), игра отличается необычайной сложностью. Это — наименынее поле, на котором игра не может закончиться вничью, поскольку игрокам необходимо построить девять (нечетное число) квадратов. Существует ли выигрышная стратегия для первого или второго игрока, насколько мне известно, пока еще не установлено.

Замечательную игру, в которой также приходится соединять точки линиями, придумал профессор Д. Гейл. Я беру на себя смелость назвать ее игрой Гейла. На первый взгляд кажется, что игра Гейла очень похожа на упоминавшуюся в нашей книге топологическую игру в гекс. В действительности же игра Гейла (рис. 123) имеет совершенно иную природу.

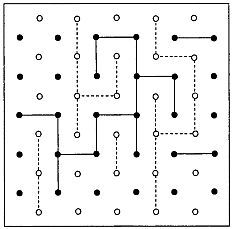
Рис. 123 Топологическая игра Гейла.

На прямоугольном поле изображены узлы двух квадратных решеток, вдвинутых друг в друга: узлы одной решетки черные, а узлы второй — любого другого цвета (на рис. 123 последние показаны белыми кружками, а соединяющие их линии — пунктиром). Игрок А наносит ломаную черным карандашом. За один ход он соединяет отрезком прямой две соседние черные точки по вертикали или по горизонтали. Его цель — соединить непрерывной ломаной левый и правый края поля. Игрок В наносит свою ломаную цветным карандашом. Его задача заключается в том, чтобы соединить верхний и нижний края поля. Линии противников не должны пересекаться. За один ход каждый игрок может соединить лишь две соседние точки. Победителем считается тот, кто первым соединит непрерывной линией свои края поля. На рис. 123 показан случай, когда победителем стал игрок с цветным карандашом.

В игру Гейла можно играть на поле любых размеров, хотя на маленьких полях (меньших, чем поле на рис. 123) ситуация слишком легко поддается анализу, чтобы игра представляла интерес для кого-нибудь, кроме новичков. Можно доказать, что при любых размерах поля всегда существует стратегия, обеспечивающая верный выигрыш первому игроку. Доказательство проводится так же, как и доказательство существования выигрышной стратегии для первого игрока при игре в гекс. К сожалению, ни одно из доказательств не дает ни малейшего намека на то, как найти оптимальную стратегию.

* * *

В 1960 году в продаже появилась доска для игры Гейла, изображенная на рис. 123; называлась она «Bridgeit».[41] Точки на доске были выпуклыми и соединялись с помощью маленьких пластмассовых мостиков, длина которых позволяла соединять лишь две соседние точки. Это позволяло вносить в игру интересные изменения, подробное объяснение которых давалось в прилагаемой инструкции.

Каждый игрок ограничен определенным числом мостиков, например 10-ю мостиками. Если после того, как «построены» все 20 мостиков, ни одному из игроков не удалось добиться победы, игру продолжают, сдвигая при каждом ходе по одному мостику в новое положение.

В 1951 году, за семь лет до того, как игра Гейла была описана мной в Scientific American, профессор Клод Э. Шеннон построил первого робота, который с успехом играл в игру Гейла (сам Шеннон называл ее «Птичья клетка»). Робот играл превосходно, хотя и не совершенно. Основным элементом робота было несложное аналоговое вычислительное устройство на сопротивлениях. В 1958 году два инженера из Иллинойсского технологического института У. А. Дэвидсон и В. Ч. Лэфферти спроектировали другого робота, также игравшего в игру Гейла. Не зная ничего о машине Шеннона, они положили в основу своего проекта тот же принцип, что и Шеннон.

Принцип этот заключается в следующем. Цепь сопротивлений соответствует линиям, которые может провести во время игры один из игроков, например А (рис. 124).

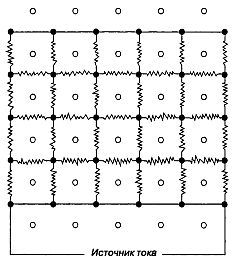
Рис. 124 Электрическая схема робота, умеющего играть в топологическую игру Гейла.

Все сопротивления одинаковы. Когда А во время очередного хода проводит отрезок прямой, соответствующее этому отрезку сопротивление замыкается. Когда игрок В в свою очередь проводит отрезок прямой, он пересекает одну из «линий» А, и соответствующий этой линии участок электрической цепи размыкается. Таким образом, если выигрывает А, то замыкается вся цепь (то есть ее сопротивление падает до нуля), а если выигрывает В, то ток в цепи полностью прекращается (сопротивление становится бесконечным). Машина либо замыкает, либо размыкает то сопротивление, на котором происходит наибольшее падение напряжения. Если же таких сопротивлений оказывается два или больше, то выбор одного из них производится случайным образом.