Итак, получаем схему:

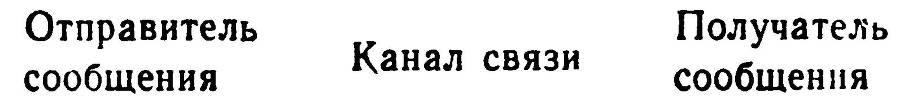
Она относится к любому средству связи, к любым собеседникам человеческого, животного или машинного происхождения. Если в глубинах космоса нас ждет встреча с неведомыми «братьями по разуму», то и тогда эта схема останется верна.

Впрочем, в нее нужно внести дополнение, прибавить еще один необходимый элемент — код.

Это слово, вероятно, вам знакомо. Знаменитая азбука Морзе является телеграфным кодом, о котором слышал любой школьник. Каждой букве русского языка соответствует набор точек и тире, например: букве «а» — точка и тире (.—), букве «е» — точка (.), букве «о» — три тире (——— ),

и т. д.

Но эти точки и тире, кодирующие русские буквы, в свою очередь, кодируются на телеграфе. Точка — быстрый нажим ключа, короткий импульс тока; тире — нажим более медленный, импульс длительный.

Впрочем, и сами буквы также являются кодовыми знаками по отношению к нашей разговорной речи. Устную речь можно кодировать и другими способами, например, записывать на магнитофонную ленту или граммофонную пластинку. Наша речь будет тогда закодирована в виде звуковых волн.

Общение невозможно, если не пользоваться каким-либо способом кодирования. Более того, необходимо, чтобы и отправитель и получатель сообщения пользовались одним и тем же кодом. Вы слышите слово «я». Нельзя считать, что это местоимение первого лица, единственного числа. А вдруг человек говорит по-немецки? Ведь тогда это будет означать «да».

Еще более многогранный пример. Один и тот же кодовый знак «!» может значить: сильный ход в шахматной нотации; знак опасности — «осторожно!» — в дорожной сигнализации; восклицательный знак в правилах правописания; знак факториала в математике, например: 5! означает 1Х2ХЗХ4Х5, 21 — это 1X2, и т. п.

Мы приводили в начале главы схему. Теперь, пожалуй, стоит несколько уточнить ее. Существует некий отправитель сообщения. Имеется устройство, которое кодирует это сообщение. Есть канал связи, через который оно передается в пространстве и во времени.

И, наконец, есть получатель сообщения и декодирующее устройство, «понимающее» знаки кода. В итоге получаем:

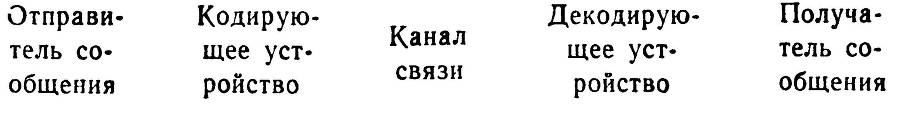
Какими бы кодовыми знаками ни записывали знаменитую теорему, ее смысл остается постоянным.

Этот смысл, математическая истина, не имеет ничего общего ни с точками и тире азбуки Морзе, ни со стенографическими значками, ни с аккуратными буквами, выведенными в ученической тетради.

Мы можем пойти на футбольный матч и видеть его своими глазами. Можем смотреть его по телевизору, можем слушать репортаж по радио. О результатах матча можно узнать от товарища, прочесть в газете «Советский спорт» или «Пионерская правда». Если вас нет дома, приятель может записать репортаж на магнитофонную ленту. Несмотря на то что матч давно закончился, вы, вернувшись домой, можете переживать весь его ход, слушая запись. .. В какие бы формы ни облекалось сообщение — в импульсы тока или звуки речи, сумели ли мы посмотреть весь матч своими глазами или узнали только о счете, — мы получили информацию.

Это слово всем вам знакомо. Но в науке оно имеет более узкий смысл, чем в обыденной жизни. Ведь и в физике слово «сила» гораздо уже, чем житейское понятие «сила». Однако такое сужение ведет к тому, что мы получаем возможность измерять информацию числами (подобно тому как в физике мы можем измерять силу). И с помощью чисел — универсального языка — мы можем привлекать к передаче, приему и переработке информации наших железных помощников — машины.

ЕДИНИЦА ИЗМЕРЕНИЯ — БИТ

Вероятно, вы читали рассказ писателя Н. Носова «Телефон». Легко можно представить себе, что его герои затеяли такую игру: один из ребят бросал монету,

а затем передавал по телефону, ка«кая сторона ее — «герб» или «решка» — оказалась сверху.

Обе стороны, если монета без вмятин, равноправны. И получатель сообщения, сидящий у телефона в соседней квартире, не знает заранее, о «гербе» или «решке» сообщит ему бросающий монету отправитель сообщения.

Информация уничтожает незнание... В нашем случае это незнание о том, какая из сторон монеты выпала, ибо обе они равноправны, или, как говорят математики, равновероятны. Информация, которая содержится в сообщении о том, какая из сторон монеты выпала, равна одному биту (сокращенное английское название «двоичный разряд» — binary digest).

Бит — это количество информации, которое содержится в сообщении, где возможно два выбора, два исхода. И оба исхода равноправны, равновероятны. Сила измеряется в динах, энергия — в эргах, масса — в граммах, время — в секундах, информация же — в битах.

Мы уже рассказывали об удивительных свойствах «машинной», двоичной арифметики, где все числа записаны в виде нулей и единиц. Теперь же стоит ознакомиться и с «машинными логарифмами» — логарифмами, у которых основанием степени взято число 2, а не 10, как в обычной школьной математике. Логарифм 2 будет равен единице; эта величина и равна одному биту, единице измерения информации.

Логарифм — это показатель степени. 2 во второй степени, то есть 4, будет равно 2 битам. Это значит, что в сообщении о том, какой масти карта, вытащенная наугад из колоды, содержится 2 бита. 23, то есть 8, равно 3 битам, 24, то есть 16, равно 4 битам, и т. д. Шахматная доска состоит из 64 квадратов. 64 — это 2 в шестой степени. Значит, если нам сообщат об одном задуманном наугад квадрате, мы получим информацию в 6 бит.

Двоичный логарифм 1 равен нулю; двоичный логарифм 3 равен 1,58496; числа 5 — 2,32193; числа 6 — 2,58496; числа 7 — 2,80735, и так далее. Значит, информация в сообщении о том, какая из шести сторон кубика выпала, равна 2,58496 бита. Точно так же можно найти, пользуясь таблицей двоичных логарифмов, значение в битах любого числа выборов.

ЗАЧЕМ НУЖНЫ ЛОГАРИФМЫ!

Но, может быть, проще обходиться без логарифмов? Ведь и так ясно, что чем больше выборов, чем больше неопределенности, тем больше информации несет сообщение, уничтожающее, «снимающее» эту неопределенность. А количество информации измерять просто числом возможных выборов, и только.

Разумеется, можно выбрать и такую меру. Но у нее есть явное неудобство по сравнению с мерой логарифмической.

Информацию, выраженную в битах, можно складывать и вычитать. Скажем, в сообщении о выборе из восьми возможностей содержится на 2 бита больше, чем в сообщении о выборе из двух исходов, так как 3 бита минус 1 бит равно 2 битам. Информация многих кодовых знаков равна сумме информации, которую несет каждый знак. Но если мерять информацию не логарифмически, в битах, то это было бы не так. И вот почему.

Мы говорили о равноправных, равновероятных выборах. Например, каждая из сторон монеты выпадает с равной вероятностью. Допустим, нам десять раз сообщили, какая из сторон монеты выпала при десяти подбрасываниях. Информация об этом равна 10 битам. Но не «20 выборам», если принять за единицу измерения просто число выборов.

Теория вероятностей говорит: вероятности надо не складывать, а умножать. У нас произошло десять событий, десять результатов подбрасывания монеты. И что бы узнать количество информации, которое мы получили, нужно перемножить число выборов десять раз, если мы хотим получить измерение информации в «числе выборов», а не в битах.

Гораздо проще не умножать, а складывать числа, особенно большие. Логарифмы и позволяют делать это.

Преимущество логарифмической меры стало особенно ясно после того, как в 1947 году американец Клод Шеннон заложил основы современной теории информации.