173. Второй игрок всегда может выиграть, действуя так, чтобы делить лепестки на 2 равные группы. Например, если первый игрок берет 1 лепесток, то второй игрок берет 2 противолежащих лепестка, оставляя 2 группы по 5 лепестков в каждой. Если же первый игрок берет 2 лепестка, то второй игрок берет 1 противолежащий лепесток, добиваясь того же самого результата. Далее он просто повторяет действия первого игрока. Если первый игрок берет 2 лепестка, оставляя в одной из групп комбинацию 2–1, то второй игрок берет соответствующие 2 лепестка, оставляя такую же комбинацию 2–1 во второй группе. Действуя таким образом, он обязательно выиграет последний ход.

174. Груз в ³/ ₄фунта, очевидно, равен ¹/ ₄кирпича; соответственно кирпич должен весить ¹²/ ₄= 3 фунта.

175. Четыре корабля перемещаются к центру, как показано на рисунке, дабы образовалось 4 ряда по 4 корабля в каждом. Пятый ряд – это нижняя горизонталь.

176. Каждая овальная крышка разрезается соответственно рис. 3, а затем 6 частей складываются вместе, как показано на рис. 4.

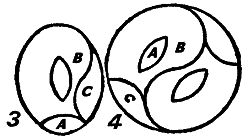
[Еще одно решение с шестью частями предложил Генри Э. Дьюдени. [33]Позднее С. Лойд нашел решение с четырьмя частями для случая с поперечными, а не продольными отверстиями. – М. Г.]

177. Можно обнаружить, что существует 372 способа прочитать Red Rum, заканчивая чтение в центре квадрата. Здесь вступает в силу любопытная особенность данной головоломки (хотя и очевидная), что существует ровно столько же способов прочитать Red Rum, сколько есть способов прочитать Murder. Следовательно, общее число способов, с помощью которых можно прочитать всю фразу, равно (372) ²– 138 384.

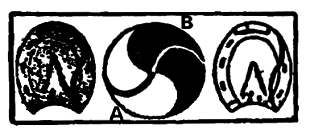
178. [Решение С. Лойда к первой головоломке с монадой показано на рисунке в центре. Крайние рисунки показывают решение третьей головоломки. Что касается его ответа на вторую головоломку, то Лойд ограничивается замечанием, что нужно провести прямой разрез от Ак 2? как показано на среднем рисунке. Каким образом найти точки А и В икак доказать, почему при этом Инь и Ян делятся на две равные по площади части, подробно разобрал Генри Э. Дьюдени. [34]– М. Г.]

179. [Составить уравнения к этой задаче труднее, чем может показаться на первый взгляд. Если х– расстояние от гостиницы до придорожной станции, то пока дилижанс стоит на станции 30 мин, человек проходит х– 6 миль. Следовательно, скорость человека составляет 2х –8 миль в час. Поскольку человек проходит 4 мили за то время, пока дилижанс проезжает хмиль, мы можем выразить скорость дилижанса в виде х(х-4)/2.

Теперь, обозначив через урасстояние от станции до Пайктауна, мы можем выписать два уравнения относительно хи у.В первом уравнении мы приравняем время, которое требуется человеку, чтобы пройти все расстояние минус 1 милю, ко времени, которое нужно дилижансу, чтобы проехать все расстояние плюс 30 мин. Во втором уравнении мы приравняем время перехода человека от станции до Пайктауна плюс 15 мин ко времени, за которое дилижанс преодолеет то же самое расстояние плюс 30 мин. Решая уравнения, мы получим для хзначение, равное 6, а для у– равное 3, так что расстояние от гостиницы до Пайктауна составляет 9 миль. Дилижанс едет со скоростью 6 миль в час, а скорость человека равна 4 милям в час. – М. Г.]

180.Два кувшина уравновешиваются тремя блюдцами, так что вес одного блюдца равен 2/3 веса кувшина. Теперь добавим на каждую чашу весов второго рисунка по стакану; при этом в левой чаше окажутся те же предметы, что и в левой чаше первого рисунка. Это означает, что вес кувшина равен весу блюдца и двух стаканов, а поскольку вес блюдца равен 2/3 веса кувшина, то вес двух стаканов равен оставшейся 1/3Следовательно, вес каждого стакана равен 1/6веса кувшина.

На первом рисунке мы видим, что стакан (1/6 веса кувшина) и бутылка уравновешивают кувшин; отсюда мы находим, что вес бутылки составляет 5/6 веса кувшина. Таким образом, чтобы уравновесить бутылку на последнем рисунке, требуется 5 стаканов.

181. Дополнительное количество спиртного, купленное агентом, увеличило стоимость всего запаса до 343 долларов. К этой сумме он сделал надбавку в 10 %, что привело к общей продажной стоимости, равной 377,3 доллара. Агент продал спиртного на 285,8 доллара, а на руках у него осталось напитков на 91,5 доллара, как и показано на рисунке. Стоимость этого остатка без 10 %-й надбавки составляет 83,18 доллара. Вычитая ее из 343 долларов (общей стоимости спиртного), мы находим стоимость проданного спиртного – 259,82 доллара. Мы вычитаем это значение из общей продажной стоимости в 285,8 доллара и находим, что доход города на продаже спиртного составил 25,98 доллара.

Это можно проверить следующим образом. Доход в 25,98 доллара плюс аванс в 12 долларов и 59,5 доллара стоимости напитков дают в сумме 97,48 доллара. Отсюда мы вычитаем комиссионные агента, равные 14,29 доллара, что дает стоимость оставшегося спиртного в 83,19 доллара и показывает, что расчеты агента были правильными в пределах 2 центов.

182. У леди в начале прогулки было 42 цента.

183. Дети были настолько не в ладах с календарем, что отправились в школу воскресным утром!

184.[Пусть хозначает общее число столбов, а у– число часов, за которое автомобиль проезжает 3 5/8 мили. Автомобиль минует хстолбов за учасов, то есть х/устолбов в час, или х/60 устолбов в минуту. Поскольку нам известно, что число столбов, мимо которых автомобиль проезжает за минуту, умноженное на 3 5/8, равно его скорости, выраженной в милях в час, мы можем составить следующее уравнение: 3 ⁵/ ₈ х/ 60у= 3 ⁵/ ₈ / у.

Произведя сокращение на общий множитель в левой и правой частях, мы находим, что х= 60.

Поскольку линия длиной в 3 5/8 мили, или в 19 140 футов, [35]содержит 60 столбов, то, разделив 19 140 на 60, мы находим, что расстояние между двумя соседними столбами составляет 319 футов. Скорость автомобиля, как и длина линии, оказывается не существенной. Однако решение задачи не единственно, если только мы не предположим, что счет столбов, проезжаемых за минуту, начинается и заканчивается в точке, расположенной в промежутке между столбами, и что аналогично определяется и длина телеграфной линии. – М. Г.]

185. Вот эти 5 нечетных «цифр», которые в сумме дают 14:

186. На рисунке показан ответ к этой удивительно трудной головоломке.

187. Шахматную доску можно разделить на 18 различных частей, как показано на рисунке.

[Существует много разных способов, какими можно разделить доску на 18 различных частей. В качестве интересного упражнения читатель может попытаться найти доказательство того, что 18 – действительно максимальное число. – М. Г.]