Рис. 78. Поворот звёздной орбиты меняет форму кривой ускорения a rи блеска m.
Теперь о причинах плавного изменения периода цефеид. Здесь снова дело в приливных гравитационных силах, под действием которых орбиты звёзд в тесных двойных системах постепенно расширяются (такой эффект реально выявлен астрономами у короткопериодических двойных звёзд и у Луны, которая, постепенно отдаляясь от нас, увеличивает продолжительность месяца [28]). Соответственно, нарастает орбитальный период и равный ему период колебаний блеска. У той же Полярной период ежегодно увеличивается на 8 секунд. Как видим, Полярная — весьма интересный и даже ключевой объект ("Природа" 2005, № 7), — не только как звезда с северного полюса мира и ближайшая к нам цефеида, но и как одно из главных подтверждений гипотезы Белопольского о двойственности цефеид. Не зря, Полярная была "любимицей" Белопольского — предметом его пристального внимания [17, 51]. Именно Белопольский первым обнаружил, что Полярная входит в двойную систему, где второй компонент — карлик главной последовательности с периодом обращения в 30 лет. Однако, колебания блеска с периодом в 4 дня у Полярной, вероятно, вызваны более близким и невидимым спутником (звездой или планетой). Не исключено, впрочем, что именно орбитальное движение Полярной в системе карлика с нарастающим a rвызывает вековые вариации: постепенный рост видимого периода её мерцаний T΄= T(1+ La r/ c 2), с медленным падением средней яркости пропорционально T΄/T, по эффекту Ритца. Точно так же, ритц-эффект может плавно наращивать или снижать период миганий и у других цефеид и переменных звёзд, входящих в кратные системы.
Иногда, вместо плавных, наблюдаются скачкообразные изменения периодов цефеид, невозможные в ТП [158]. Зато, если цефеиды — двойные, такие сдвиги периода вполне могут быть вызваны столкновением звезды с малым космическим телом. Удар скачком меняет скорость звезды, её орбиту и период обращения, но, за счёт малой массы врезавшегося тела, это изменение периода обычно мало в сравнении с самим периодом. Таким образом, все странные пертурбации мигающих звёзд — это следствие изменения размера, формы, наклона и поворота их орбит.
К слову о периоде, БТР объясняет и знаменитую зависимость период-светимость: чем выше период колебаний блеска звезды, тем выше её абсолютная яркость. Связь "период-светимость" и сделала цефеиды маяками космоса: определив по периоду действительную яркость цефеиды и, сравнив с видимой, находят удалённость звезды. Но почему же период выше у ярких цефеид? Причина в том, что цефеиды — это очень тесные системы, где размеры звёзд и их орбит сопоставимы. Поэтому, более крупные и яркие цефеиды и орбиты имеют большие, а, значит, — и периоды. А вот для звёзд типов Миры Кита и RV Тельца, имеющих периоды около года и широкие орбиты, основное значение приобретает уже масса звезды. Поэтому, чем ярче, массивней звёзда, тем быстрей крутятся возле неё спутники, и тем меньше период миганий. Недаром, у звёзд указанных типов зависимость "период-светимость" — обратная в сравнении с цефеидами: чем выше период, тем меньше яркость [158], о чём в теории пульсаций упоминать не любят, поскольку не могут объяснить.
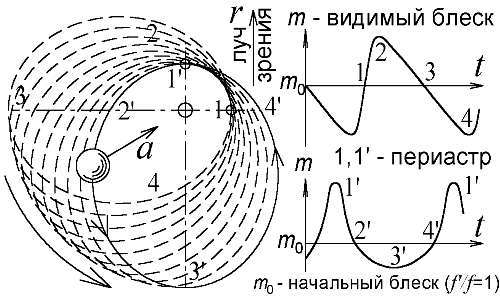
Используя ТП, нельзя объяснить даже форму кривых блеска. У цефеид и звёзд типа RR Лиры эти кривые часто имеют отчётливый горбик (Рис. 75) — вторичный максимум [157]. Истолковать его можно, лишь считая цефеиды двойными. Обычно, у двойных звёзд, образующих цефеиды, заметна лишь главная, более яркая звезда, тогда как блеск звезды-спутника, или, даже, — планеты, совершенно незаметен на её фоне, что предполагал ещё Белопольский [51]. Но, в случаях, когда яркость главной звезды и спутника сопоставимы, их кривые блеска, слагаясь, дадут два максимума и минимума (Рис. 79). Существованием двух колебаний, наложенных и сдвинутых по фазе, объясняют вторичный максимум и в теории пульсаций, но не могут объяснить, откуда берётся сдвинутое по фазе колебание [102, с. 89]. А БТР объясняет не только этот фазовый сдвиг (лучевые ускорения пары звёзд колеблются в противофазе), но и его изменение: смещение горбика в зависимости от периода цефеиды [157, 158]. Просто положения максимумов на кривых блеска главной звезды и звезды-спутника зависят от их орбитальной скорости, а, значит, — от периода их обращения. Тот же эффект вторичного максимума может создать и одна звезда. Ведь кривая ускорений, как показывает компьютерное моделирование, имеет плавную форму лишь у звёзд с орбитами малого эксцентриситета ε. При ε=0,3 и более на кривой ускорений возникает горбик (Рис. 75), переходящий и на кривую блеска. Причём, моделирующая программа позволяет наблюдать постепенное смещение вторичного максимума по кривой блеска — при увеличении периода цефеиды, в полном согласии с наблюдениями. Но, несмотря на успехи БТР в разгадке форм кривых блеска цефеид, эффекта Блажко и других закономерностей и аномалий, некоторые авторы [82] ещё пытаются нас убедить, что характер колебаний яркости цефеид не совпадает с предсказаниями баллистической теории. На деле же, такие нестыковки всегда отличали как раз пульсационную теорию цефеид Эддингтона.
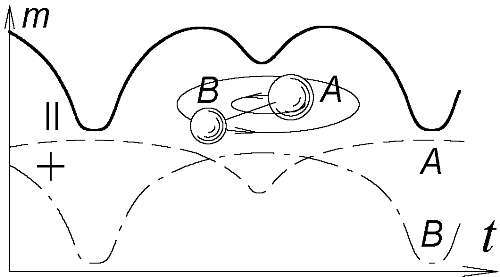
Рис. 79. Блеск звёзд A и B меняется в противофазе, что в сумме даёт сложную кривую блеска m, как для β Лиры и W Большой Медведицы.
Другая странность колебаний блеска в том, что иногда они происходят сразу с двумя периодами: одно колебание налагается на другое, как, скажем, у AC Андромеды [158]. БТР легко обходит этот камень преткновения теории пульсаций. Ведь, если главная звезда имеет не один, а два спутника с разными периодами обращения P 1и P 2, то вызванные их притяжением смещения главной звезды возле центра масс тоже происходят с двумя периодами, отчего двойной период колебаний приобретут кривые ускорений и блеска (Рис. 80.1). И такие спутники у переменных звёзд реально выявлены, скажем, — у σ Скорпиона, причём их орбитальные периоды действительно оказались связаны с периодом колебаний блеска [27, с. 67]. Два периода дают и кратные системы, где один компонент двойной звезды сам является парным (Рис. 80.2). Такие трёх-, четырёхкратные системы в космосе — не редкость. При этом, быстрые периодичные колебания яркости наложены на долгопериодические вариации среднего блеска звезды, реально открытые у DF Лебедя и других звёзд типа RV Тельца [158]. Наличием двух спутников, особенно, если их орбитальные периоды близки или кратны, можно объяснить и периодичные изменения формы кривой блеска (эффект Блажко), а также загадочное усиление и прекращение колебаний блеска цефеид, за счёт сложения кривых ускорений и блеска от обращения двух спутников (аналогично эффекту биений от сложения двух колебаний). Наконец, если главная звезда обладает более чем двумя спутниками, скажем четырьмя или пятью, то их притяжение создаст кривую ускорений и блеска столь сложную, что колебания яркости покажутся случайными, неправильными. Такие неправильные переменные, говорящие против ТП, реально выявлены в наблюдениях [158].
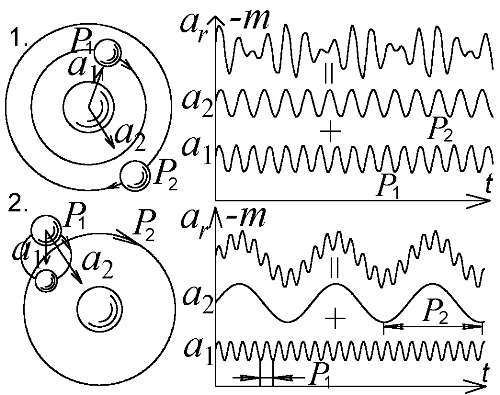
Рис. 80. В кратных системах сложение кривых ускорений порождает сложные формы колебаний ускорений ar и блеска m по ритц-эффекту.
Вообще, оказывается, астрономы давно уже открыли двойные звёзды, в которых плавные колебания блеска вызваны орбитальным движением. Примером таких звезд служат β Лиры и W Большой Медведицы [76, 158]. У β Лиры нашли плавные колебания яркости, подобные цефеидным, и спутник, обращающийся с тем же периодом в 13 дней. А у W Большой Медведицы звезда-спутник обращается с периодом 0,33 дня (оба периода типичны для цефеид и звёзд типа RR Лиры). Их непрерывные плавные колебания блеска нельзя объяснить эпизодическими затмениями звезды спутником. Поэтому, астрономы приняли следующее надуманное объяснение: звёзды в системе имеют вытянутую форму, за счёт чего при вращении их видимая яркость меняется. Кроме того, систему окружили газовым кольцом, приняли ещё уйму допущений, и, всё равно, модель мало соответствовала наблюдениям.