Так, для круговой орбиты кривая лучевого ускорения a rимеет форму синусоиды: a r= a×sin(2π t/ P) (Рис. 68. а), и, потому, видимая яркость тоже периодически меняется, пропорционально T/T΄=1/[1+ La×sin(2π t/ P)/ c 2]. Причину изменения яркости за счёт временной фокусировки света можно пояснить и наглядно. От перекоса кривой лучевых скоростей (Рис. 67. а) пара точек 1 и 2, соответствующих началу и концу промежутка времени T, смещаются, причём в разной степени, и расстояние между 1 'и 2 ', измеренное вдоль оси времени t, даст видимый интервал времени T', отличный от T. Свет, испущенный звездой за период T, воспринимается в течение иного времени T', и, потому, он станет казаться пропорционально T/T΄ярче или слабее, в зависимости от положения звезды.
Но, именно такая переменная яркость, периодичная кривая блеска, как заметил Секерин, характерна для переменных звёзд типа цефеид. По Секерину, цефеиды — это не что иное, как двойные звёзды. Впервые эту мысль высказал уже упомянутый выше русский астрофизик А.А. Белопольский (Рис. 54): сняв у цефеид кривые лучевых скоростей, он подметил их сходство с таковыми у двойных звёзд и предложил гипотезу, по которой именно вращением цефеид в двойных системах вызваны колебания их блеска и спектра [51]. Но от его точки зрения отказались, посчитав, что цефеиды — это пульсирующие, периодично раскаляющиеся звёзды. Учёт эффекта Ритца позволяет вернуться к гипотезе Белопольского. Если цефеиды — это двойные звёзды, то простое толкование получат многие их странности и особенности. Так, легко объяснятся синхронные с колебаниями яркости колебания температур и лучевых скоростей цефеид (Рис. 74): и то и другое суть следствия эффекта Ритца, — смещения, соответственно, спектров излучения и поглощения. И все эти колебания — кажущиеся. Видимо, и предсказанные БТР искажения в движении двойных звёзд не были обнаружены только потому, что, когда такие искажения становятся заметны за счёт перекоса кривых скоростей (Рис. 67. а), начинает заметно колебаться и яркость звезды, и её считают уже не двойной, а цефеидой. Сравнение типичных кривых скоростей цефеид (Рис. 74. б) с Рис. 67. аподтверждает баллистический принцип, по которому у двойных звёздных систем с круговыми орбитами, за счёт кажущегося изменения масштаба времени, кривая лучевых скоростей сильно скошена (эффект Барра), — наклонена вправо [33, 158]. Кстати, и сам Барр в своей статье 1908 г.связал перекос графиков скоростей спектрально-двойных — с колебаниями блеска цефеид, которые по гипотезе Белопольского считал тоже двойными звёздами и именно их орбитальным и осевым вращением объяснял колебания блеска.
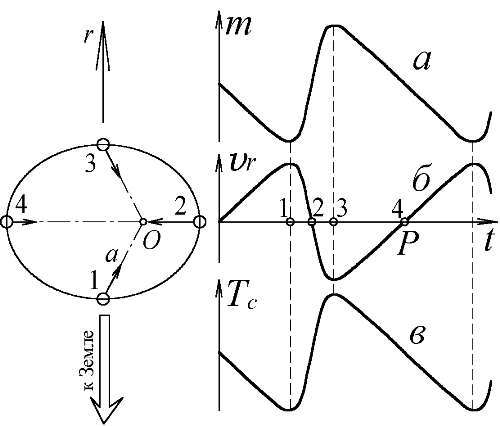
Рис. 74. Наблюдаемые у цефеид колебания блеска m, скорости v rи температуры T cполучаются в БТР как естественное следствие эффекта Ритца для двойных звёзд. Они представляют собой лишь иллюзию, созданную преобразованием частоты и масштаба времени от переменного ускорения a r.
Если колебания блеска и спектра вызваны единой причиной, — эффектом Ритца от ускоренного движения звезды по орбите, то должна быть определённая связь между характеристиками кривых блеска, "лучевых скоростей" и температур. И, действительно, известно, что, вместе с нарастанием амплитуды колебаний блеска, растёт амплитуда колебаний температур и лучевых скоростей [65, 102, 140]. Рассмотрим звезду, расположенную на расстоянии L, движущуюся по круговой орбите с ускорением aи обладающую средней яркостью I. Тогда, по ритц-эффекту временной фокусировки света (§ 2.11), величина яркости в максимуме есть I(1+ La/c 2), а в минимуме I(1- La/c 2). Таким образом, глубина модуляции яркости Δ I/I=2 La/c 2. Те же преобразования испытывает и частота, и длина волны. Поэтому, в спектре излучения звезды спектральный максимум λ maxсмещается то в красную, то в синюю сторону с размахом Δ f/f=Δλ/λ=2 La/c 2. То есть, звезда будет казаться то синее, то краснее, меняя цвет синхронно с яркостью. Эти вариации спектра излучения интерпретируют как изменение температуры звезды, хотя реально спектральный анализ, по закону смещения Вина T cλ max= b=0,003 м·K, даёт лишь оценочную цветовую температуру тела T c, часто не совпадающую с реальной температурой [74, 136]. Согласно закону Вина: чем краснее излучение тела, чем дальше его цвет и отвечающее ему значение λ maxсдвинуты в длинноволновую область, тем ниже температура тела T c, в чём легко убедиться, наблюдая остывание раскалённого над пламенем металлического прутка. Соответственно, периодичные смещения спектрального максимума цефеиды расценивают как колебания её температуры Δ T c/T c=Δλ max/λ max =2 La/c 2. То есть, глубины модуляции температуры T cи яркости Iдолжны быть, согласно БТР, одинаковы, что и наблюдается у цефеид. Но, ещё раз отметим, что это лишь видимые колебания параметров, вызванные эффектом Ритца, тогда как реальная яркость и температура цефеид (отличная от цветовой) — не меняются.
Но между амплитудой колебаний блеска и лучевых скоростей может уже и не быть столь точного соответствия. Спектр поглощения испытывает гораздо меньшие колебания, чем спектр излучения. Причина этого, по-видимому, в том, что, если спектр излучения наблюдают преобразованным на всём пути следования, то спектр поглощения может создаваться слоями газа, расположенными гораздо ближе к Земле. Соответственно, смещения, вызванные эффектом Ритца, будут много меньше. Не исключено, поэтому, что колебания спектра поглощения вызваны, в основном, эффектом Доплера, а не Ритца. Интересно отметить, что сам Х. Доплер объяснял различие цвета звёзд в двойных системах их движением и открытым им эффектом, смещающим цвет звезды в зависимости от её положения на орбите и лучевой скорости то в красную, то в синюю сторону. Эта интересная гипотеза критиковалась многими и тормозила признание эффекта Доплера [153]. Но, выходит, чешский физик был в чём-то прав: именно такие колебания цвета, вызванные движением звёзд в двойных системах, мы и наблюдаем у цефеид. Только вызывает их не эффект Доплера, а — эффект Ритца, или ЭДР, поскольку скорости звёзд недостаточны для сильного изменения их спектра, тогда как ускорения и эффект Ритца за счёт большой удалённости Lменяют цвет весьма заметно.
Наконец, была уверенно обнаружена и связь амплитуды блеска со степенью асимметрии кривой блеска и кривой скоростей. Все цефеиды имеют тенденцию резко наращивать яркость и долго снижать её до прежнего уровня. Степень этой асимметрии, как оказалось, растёт с увеличением амплитуды колебаний блеска. Это так же находит объяснение в рамках БТР. Большинство двойных звёзд имеет круговую орбиту и потому должны иметь синусоидальную кривую лучевых скоростей. Однако, видимое изменение масштаба времени от эффекта Ритца приводит к тому, что кривые лучевых скоростей, а, значит, и кривые блеска становятся асимметричными, перекошенными (эффект Барра, Рис. 67). И, чем выше этот перекос, тем выше сопровождающие его по эффекту временной концентрации света вариации яркости. Именно этим объясняется наблюдаемая зависимость, впервые отмеченная тем же Барром в его статье 1908 г. Поэтому, классические цефеиды, имеющие резко асимметричные спектральные кривые, показывают сильные колебания блеска. Зато переменные звёзды с почти симметричной, синусоидальной кривой блеска, имеют слабые колебания яркости, как, например, малоамплитудные цефеиды типа ζ Близнецов [157, 158]. Этот эффект легко наблюдать на трёхмерной диаграмме клистрона, где хорошо видно, что, по мере нарастания амплитуды колебаний плотности потока электронов, увеличивается и асимметрия волн, становящихся из синусоидальных — коноидальными, с острыми пиками (Рис. 72, Рис. 73).