Другой причиной асимметрии кривой блеска цефеид могут быть эффекты взаимодействия света подвижной звезды со средой. Как было показано Фоксом, свет, проходя через межзвёздный газ, в ходе переизлучения атомами, постепенно теряет дополнительную скорость, приданную звездой (§ 1.13). Это тормозящее действие среды оказывается разным для лучей света, испущенных с разной частотой и скоростью в моменты приближения и отдаления звезды. Поэтому, преобразование кривой лучевых скоростей усложняется в сравнении с Рис. 67, становясь нелинейным, что и создаёт добавочную асимметрию кривых блеска и лучевых скоростей цефеид, тем ярче выраженную, чем выше амплитуда колебаний лучевой скорости и блеска. Вот почему, яркость цефеид нарастает быстро, а спадает медленно: гребни световых волн (колебаний интенсивности) не только нарастают по мере движения, но и укручают передний фронт, подобно волнам морского прибоя, становящимся, по мере движения, резко асимметричными, из-за нелинейных эффектов при трении о дно (§ 2.11). Подобное торможение средой света цефеид надо учитывать ещё и потому, что оно ведёт к сокращению эффективного расстояния L, на котором идёт преобразование света по эффекту Ритца. Временная фокусировка света происходит не на всём пути, а лишь на начальном его участке, на эффективном расстоянии L(составляющем по оценкам Дж. Фокса порядка светового года [2]), по прохождении которого скорость света приводится средой почти к значению c, и колебания яркости практически перестают нарастать. Этот эффект особенно существенен для определения расстояний до цефеид по эффекту Ритца (§ 2.13).
Итак, принцип работы мигающих звёзд, — этих "маяков Вселенной", как их порой называют, состоит в чисто механическом сложении скорости света со скоростью испустившей его звезды. Изучим попристальней эти мигающие, пульсирующие звёзды-маяки. Кроме цефеид, к ним относят ещё звёзды типов RR Лиры, RV Тельца и Миры Кита [158]. Пульсирующими все эти звёзды назвали потому, что периодичные спады-нарастания их яркости и температуры принято связывать с пульсацией (расширением-сжатием) этих звёзд. Но теория пульсаций (ТП), разработанная уже упоминавшимся астрофизиком А. Эддингтоном и необоснованно сместившая теорию цефеид Белопольского [51], имеет массу нестыковок. К примеру, если бы звезда пульсировала, то наибольшей температурой и яркостью она б обладала в момент предельного сжатия. Реально же, звезда ярче всего в момент расширения с максимальной скоростью, если судить по эффекту Доплера (Рис. 75).
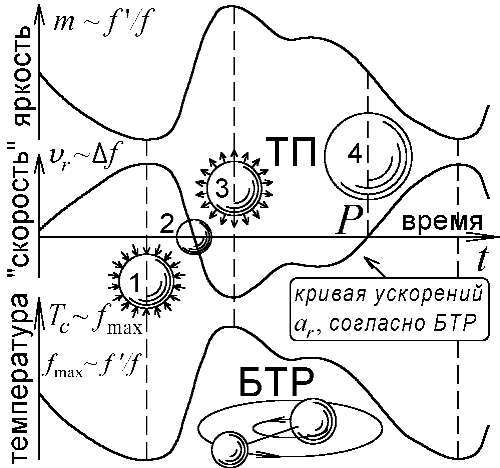
Рис. 75. Синхронные колебания яркости, лучевой скорости и температуры цефеид, сходные по форме и не объяснимые по теории пульсаций, прямо следуют из БТР.
Впрочем, теоретики, во главе с известным махинатором Эддингтоном, быстро подогнали факты к теории формальным приёмом: посчитали, что внешние и внутренние слои звезды пульсируют по-разному. Другое несоответствие их тоже не остановило. Выяснилось, что пульсации звёзд, как любые свободные колебания, должны довольно быстро затухать, чего реально никто не наблюдал. Пришлось выдумать весьма сложный и надуманный механизм поддержания автоколебаний звезды. В ходе таких формальных подгонок и возникла современная теория звёздных пульсаций, при всей своей сложности и искусственности способная объяснить лишь очень немногие особенности цефеид.
Совсем иная картина складывается в БТР, где из гипотезы А. Белопольского, считавшего цефеиды двойными звёздами, сразу вытекают все их свойства. Напомним, что Ритц предсказал эффект влияния лучевого ускорения arисточника на его частоту fи яркость, меняющихся пропорционально множителю f'/ f= T/ T'=1/(1+ La r/ c 2), где L— расстояние до источника, а c— скорость света. Как показано выше, у цефеид с периодом в десятки дней этот эффект изменения частоты намного превосходит доплеровский. Поэтому, движение двойных звёзд по орбите с переменным лучевым ускорением должно вызвать сильные колебания (с периодом равным орбитальному) их видимой яркости и синхронные смещения спектральных линий, дающих по эффекту Доплера "скорость" звезды (Рис. 76). Не случайно, кривые "блеска" и "лучевых скоростей" (реально же ускорений) — это зеркальные копии друг друга (Рис. 75). Кстати, ТП их сходства объяснить не может, поскольку в случае пульсаций кривая блеска должна формой повторять колебания радиуса звезды, а не её скорости.
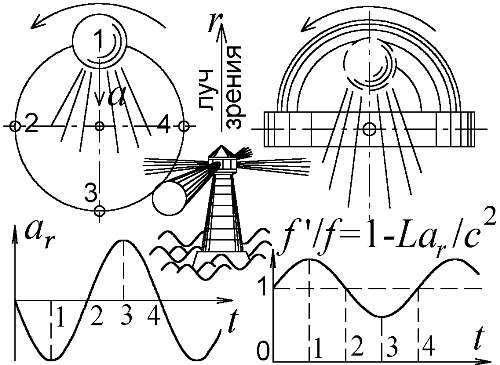
Рис. 76. Звезда, крутящаяся по орбите, словно прожектор маяка, создаёт ускорением a rколебания блеска и частоты f пропорциональные f'/f.
Как видели, от сильного сдвига частоты, спектра цефеид будет казаться, что меняется их температура T c, оцениваемая по цвету звезды (её спектральному максимуму f max). И, в момент предельной величины яркости и ускорения, когда спектр максимально смещён в синюю сторону, покажется, что звезда горячей всего. Вот почему, колебания "яркости", "лучевой скорости" и "температуры" — идентичны и синхронны [33]. Если у колебаний и есть небольшие расхождения формы и фазы, то они вызваны разной степенью взаимодействия (поглощения и переизлучения) лучей разного цвета, имеющих разную скорость, с промежуточной средой (облаками газа), и ещё тем, что кривые блеска и температур дают общее изменение яркости и спектра двойной звезды, а не одного компонента, — как кривая лучевой скорости. Согласно БТР, все эти колебания не затухают по той простой причине, что порождающее их орбитальное вращение — это пример наиболее стабильного, почти вечного движения. Так что, маяки цефеид будут мерцать вечно, пока не "перегорит" звезда. Есть, правда, цефеиды, которые по неясным причинам прекращают менять яркость, а, затем, нередко, вновь начинают ("Наука и жизнь" 1967, № 7). Такова, к примеру, Полярная звезда. Этот древний маяк и ориентир моряков оказался тоже цефеидой. В начале XX в. её яркость раз в четыре дня менялась на 15 %, а к концу XX века звезда почти перестала мигать: колебания яркости Δ I/ Iупали до 2 % ("Природа" 2005, № 7). Ныне Полярная восстанавливается: Δ I/ Iуже стало 4 %, а в обозримом будущем вновь достигнет 12 %. Объяснение подобного непостоянства цефеид представляет серьёзную проблему для ТП, но не для БТР.
Всё дело в том, что в тесных двойных звёздных системах, к которым, очевидно, относятся цефеиды, орбиты из-за огромных гравитационных и приливных сил часто претерпевают быстрые изменения, что отражается на кривой лучевых ускорений и, следовательно, на колебаниях блеска. В частности, плоскость звёздной орбиты может менять наклон к лучу зрения, подобно тому, как кренится в разные стороны диск прецессирующего волчка (Рис. 77). Точно так же, к примеру, наклоняется то туда, то обратно в ходе прецессии плоскость орбиты Луны [28]. Вот и плоскость звёздной орбиты в один момент может предстать видимой в плане (перпендикулярно лучу зрения), а в другой — с ребра. В первом случае лучевые ускорения занулятся, а потому исчезнут и колебания блеска. Когда же орбита чуть повернётся, колебания яркости вернутся.
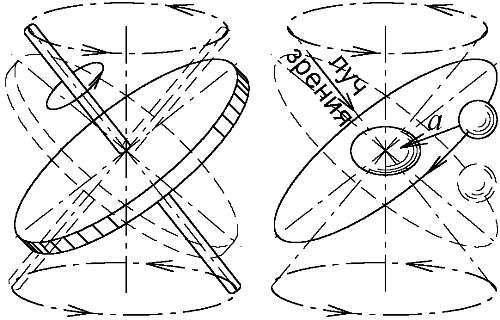
Рис. 77. Изменение наклона к лучу зрения плоскости волчка и звёздной орбиты.
Поскольку у звёзд, как у Луны, прецессионное вращение орбит цикличное (сделав полный оборот, орбита займёт прежнее положение), то и степень колебаний блеска цефеид должна меняется периодично. Особенно такие вариации характерны для звёзд типа RR Лиры и карликовых цефеид, — переменных с периодами в несколько часов. И не удивительно, ведь столь малый период обращения говорит о близости компонент двойной звезды и ощутимости гравитационного возмущения орбит. Не зря, у таких звёзд обнаружены и другие необъяснимые теорией пульсаций аномалии: периодично меняется форма кривой блеска (эффект Блажко) и очень медленно — период его колебаний [158]. Эти вариации легко объяснимы в БТР. В тесных двойных системах орбиты звёзд поворачиваются, подобно перигелию орбиты Меркурия (§ 2.3), только гораздо быстрее. Впервые такое явление постепенного смещения периастра двойных звёзд обнаружил всё тот же Белопольский [17]. По мере вращения орбиты, меняется, в зависимости от угла поворота, — форма кривой ускорений (Рис. 68) и, соответственно, — форма кривой блеска (Рис. 78). Когда орбита сделает полный оборот, кривая блеска примет исходную форму. То есть, в полном соответствии с эффектом Блажко, вариации кривой должны периодично повторяться.