Особое внимание Степанцов уделял проблеме практически неизбежной паники среди людей в случае возникновения чрезвычайных ситуаций в общественном месте. Главной задачей исследователя было смоделировать ситуацию с беспорядочным движением большой неорганизованной группы людей (то есть толпы), чтобы выявить те элементы и особенности конструкций, которые могут спровоцировать давку или "пробку". Степанцов полагает, что помимо общего потока пассажиров в проектировании городских пешеходных коммуникаций стоит также учитывать данные детального мониторинга движения потоков на отдельных участках.
Наиболее уместным решением в данном случае является использование класса математических моделей, известных как "клеточные автоматы", которые активно применяются, например, в газодинамике. Степанцов считает, что моделирование ситуаций с активным участием людей на данном этапе научного прогресса практически невозможно, так как исследователю приходится иметь дело с критически большим количеством скрытых факторов. Однако по мере увеличения количества участвующих в модели людей роль рациональных и иррациональных факторов, описывающих поведение отдельного человека, снижается, и поведение группы может быть описано вероятностным образом, то есть спрогнозировано. Это характерная иллюстрация действия закона больших чисел. Даже если исследователь не учитывает причин, которые могут заставить индивидуума действовать нестандартным образом, его поведение вряд ли скажется на действиях общей группы.
Клеточные автоматы – дискретные системы, то есть параметры, описывающие пространство и время, принимают значения из конечного небольшого набора. Клеткой называется узел пространственной решетки, ближайшие ячейки называются соседями. Каждому узлу присваивается некоторый набор значений, описывающий его текущее состояние, которое может изменяться по заданным правилам в зависимости от состояния соседей.
В данном случае клеточный автомат имеет два состояния клетки (наличие/отсутствие в ней человека) и учитывает две составляющие движения: хаотичное и направленное. Интересно, что данные условия схожи с уже существующей моделью, описывающей диффузионные процессы (окрестность Марголуса). Степанцов модифицировал правила этой модели, добавив к диффузионной составляющей движения направленную и представив движение частицы (человека) как суперпозицию случайного и направленного перемещения.
Далее была программно реализована работа клеточного автомата и исследованы некоторые модельные задачи. Так, на рис. 1 отражена ситуация, в которой люди выбегают из узкого выхода. При этом измеряется временная зависимость плотности числа людей до сужения и после. В данном случае плотность в широкой части прохода выше, а значит, данный выход может спровоцировать затор. Этого не произошло при изменении конфигурации прохода (рис. 2). Таким образом, модель позволяла описывать возникновения эффекта пробки и "отрицательной вязкости" (более быстрое движение у границ прохода).
Впоследствии Степанцов дважды вносил изменения в свою модель – в 1999 и 2003 гг. Главной целью доработки был учет решений человека, который стремится выбрать оптимальный путь к выходу, даже находясь в толпе. Раннюю версию исследователь называл моделью "слепых котят", так как выбор способа движения в заданном направлении отдавался на волю случая.
Для привнесения элементов анализа ситуации людьми выдвигается предположение, что каждый индивид старается передвигаться в нужном направлении и если видит непреодолимое препятствие или значительное скопление других людей на своем пути, то меняет траекторию движения в область с минимальными затруднениями. Для этого в модель вводится понятие "просмотра" на некое расстояние (добавляется параметр r). Если в направлении движения на этом расстоянии встречается клетка с препятствием, то она и все лежащие за ней клетки считаются занятыми. Тогда человек начинает смещаться в сторону, стараясь придерживаться общего вектора (для этого просто нужно увеличить вероятность движения в направлении выхода).
Эффективность модели также была проверена на решении тестовых задач. Так, автор исследования попробовал оценить различные профили сужения некоего коридора и выделить оптимальный угол, при котором длина сужения будет минимальной, однако достаточной для того, чтобы избежать возникновения заторов. После моделирования оказалось, что оптимальным значением угла является 45 градусов. В этом случае пробка будет возникать только при плотности потока, приближающейся к максимально возможной (рис. 3).
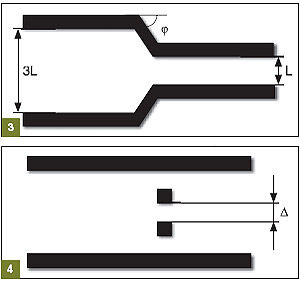
Другая задача состояла в том, чтобы определить наиболее удачное расположение двух конструкций, занимающих 40 % ширины прохода. Вместо угла в качестве искомого параметра фигурировало расстояние между этими конструкциями, а условием оптимизации было минимизирование времени прохождения определенного числа людей. Оптимальным оказалось расположение, при котором конструкции делят проход на равные отрезки (рис. 4). Степанцов рекомендовал эту модель в качестве одного из средств проверки безопасности перемещения толпы в условиях пространственных ограничений.
Для проведения соответствующих расчетов в России уже около тридцати лет используется модель движения людских потоков – ADPLV ("Анализ движения людских потоков, вероятность"), где все пути внутри здания представлены как множество взаимосвязанных элементарных участков длиною около метра, на которых в последовательные моменты времени пересчитываются параметры движения людей. На базе модели было разработано одноименное приложение для расчета времени эвакуации из здания, включая начало и завершение движения по каждому участку строения. Кроме того, ADPLV позволяет выделять участки с образованием критически высокой плотности, для которой помимо значения можно посчитать время ее образования и рассасывания, а также срок существования.
Этот софт был сертифицирован тогда еще Госстандартом РФ, однако пока более распространенной методикой подсчета остается ручное калькулирование по формулам из ГОСТ 12.1.004-91. Последний учитывает такие свойства движения толпы, как пересечение границы смежного участка пути, слияние и расчленение, а также частично позволяет принять во внимание образование и рассасывание скоплений. ADLPV более близка к реальности (см. врезку), так как позволяет рассчитать время эвакуации с учетом переформирования, растекания, неодновременности слияния, разуплотнения и неоднородности людского потока (например, наличие инвалидов).
Так, при проектировании ММДЦ "Москва-Сити" для проверки пропускной способности лестничных клеток были проведены многовариантные расчеты эвакуации при изменяющихся параметрах людских потоков и размеров путей. Планирование было реализовано при помощи специального ПО, разработанного под руководством профессора МГСУ [Московский государственный строительный институт] Валерия Холщевникова. На его счету множество публикаций на тему моделирования движения людей, а также открытие ряда количественных закономерностей между плотностью и скоростью людских потоков. При планировании эвакуационных путей требовалось определить ширину, которая позволила бы толпе беспрепятственно перемещаться даже при максимальной плотности потока. В результате получилось, что при норме 15 кв. м на человека скоплений можно избежать при ширине пролета 1,35 м и более.
Конечно, определением габаритов коридоров и лестничных проемов забота о беспрепятственном прохождении людей не ограничивается. С той или иной степенью этот аспект учитывается архитекторами при планировке местонахождения лестниц на этаже и установке противопожарных заграждений. Так, требуется, чтобы заблокированный по тем или иным причинам, в том числе в результате пожара, сегмент этажа легко и с минимальными потерями времени можно было обойти. Отдельная задача проектировщиков – обеспечение незадымляемых лестничных клеток с использованием систем подпора воздуха.