Глава 9. От структуры к функции.

Теория графов и сетевая нейронаука

В 1931 году, за три года до своей смерти, Сантьяго Рамон-и-Кахаль передал Институту Кахаля в Мадриде коллекцию своих личных вещей. В коллекции были всевозможные научные безделушки: весы, слайды, фотоаппараты, письма, книги, микроскопы, растворы, реактивы. Но самыми примечательными предметами - теми, которые станут почти синонимом имени Кахаля, - были 1907 научных рисунков, которые он создал за свою карьеру.

Большинство этих рисунков представляли собой различные части нервной системы и были получены в результате трудоемкого процесса окрашивания клеток. Для этого использовалось живое животное, которое приносилось в жертву, а его ткани консервировались. Затем кусок мозга извлекался и замачивался в растворе на два дня, высушивался и замачивался в другом растворе - содержащем серебро, которое проникало в клеточные структуры, - еще на два дня. После этого ткань мозга промывали, снова высушивали и разрезали на кусочки, достаточно тонкие, чтобы поместиться на предметном стекле микроскопа. Кахаль рассматривал эти срезы в окуляр микроскопа и зарисовывал то, что видел. Начиная с карандаша, он очерчивал на куске картона каждый уголок формы нейрона, включая толстые тела клеток и тонкие придатки, выходящие из них. Затем он затемнил клетки индийскими чернилами, иногда используя акварель, чтобы добавить текстуру и размерность. В результате получился набор призрачных силуэтов черных паукообразных на бежевом и желтом фоне.1 Точные контуры и конфигурации зависели от животного и нервных волокон, о которых идет речь; на картонных холстах Кахаля изображены более 50 видов и почти 20 различных частей нервной системы.

Эти сотни портретов отражают увлеченность Кахаля строением нервной системы. Он искал просветления в основной единице мозга - нейроне. Он зациклился на том, как они сформированы и как устроены. Сосредоточение на физических основах было для Кахаля путем к пониманию того, как работает мозг. Он считал, что функция может быть найдена в структуре.

И он оказался прав. Кахаль смог установить важные факты о работе мозга, долго и тщательно изучая его строение. Одно из его важных открытий касалось того, как сигналы проходят по нейронам. Наблюдая за различными нейронами в разных органах чувств, Кахаль заметил, что клетки всегда расположены определенным образом. Многочисленные разветвленные дендриты клетки были направлены в ту сторону, откуда поступал сигнал. Длинный одиночный аксон, напротив, направлялся к мозгу. В обонятельной системе, например, нейроны с химическими рецепторами, способными улавливать молекулы запаха, находятся в слизистой оболочке внутри носа. Эти нейроны посылают свои аксоны в мозг и контактируют с дендритами клеток в обонятельной луковице. От этих нейронов отходят аксоны в другие части мозга.

Эта закономерность, которую Кахаль наблюдал снова и снова, наводила на мысль, что сигналы идут от дендритов к аксонам. Дендриты, заключил он, действуют как приемник сигналов для клетки, а аксоны - как отправитель сигналов для следующей клетки. Кахаль был настолько ясен в этом вопросе, что добавлял маленькие стрелки к своим рисункам схем, таких как обонятельная система, указывая предполагаемое направление потока информации. Кахаль, как мы теперь знаем, был абсолютно прав.

Кахаль был одним из отцов-основателей современной нейронауки. Его вера в связь между структурой и функцией вошла в ДНК этой области. Отголоски этой идеи встречаются во всей истории нейронауки. В статье 1989 года Питер Гетинг пишет, что исследователи 1960-х годов даже на основе своих ограниченных данных могли видеть, что "способности сети возникли из соединения простых элементов в сложные сети, таким образом, из связности возникла функция". К исследованиям 1970-х годов, продолжает он, "подходили с несколькими ожиданиями: во-первых, знание о связности объяснит, как работают нейронные сети". Такое отношение сохраняется. Обзор, написанный в 2016 году профессорами Сяо-Цзин Вангом и Генри Кеннеди, заканчивается следующим утверждением: "Установление прочной связи между структурой и функцией необходимо для понимания сложной нейронной динамики".

В мозге структура существует в разных масштабах. Неврологи могут посмотреть, как нейроны соединены между собой: связан ли нейрон A с нейроном B? Можно еще больше увеличить масштаб и спросить, как взаимодействуют небольшие популяции нейронов. Или можно изучить схемы связей в масштабах всего мозга, рассматривая толстые пучки аксонов, соединяющие отдаленные области мозга. Любая из этих структур более высокого уровня может хранить секреты о функциях.

Но чтобы раскрыть эти секреты, нейробиологам нужен способ четко видеть и изучать эти структуры. То, что можно было бы счесть ограничением метода окрашивания, использованного Кахалем, - то, что он окрашивал лишь небольшое количество нейронов за раз, - на самом деле оказалось преимуществом, которое сделало его революционным. Метод, при котором окрашивались бы все нейроны в поле зрения, привел бы к черному беспорядку без видимых структур; в этом случае деревья не были бы видны. Поскольку нейробиологи перешли от изучения структуры отдельных нейронов к более сложному изучению связей, сетей и схем, они могут подвергаться еще большему риску перегруженности данными и отвлечения на неверные детали.

Однако столь необходимый метод был найден в особой области математики - теории графов. Язык теории графов предлагает способ говорить о нейронных сетях, который избавляет от многих деталей. В то же время ее инструменты находят особенности нейронной структуры, которые практически невозможно увидеть без нее. Эти особенности структуры, как считают некоторые ученые, могут натолкнуть их на новые мысли о функциях нервной системы. Поглощенные перспективами методов теории графов, неврологи в настоящее время применяют их ко всему- от развития мозга до болезней. Хотя пыль еще не осела от этого нового подхода к мозгу, его свежий взгляд на старые проблемы волнует многих.

* * *

В столице Восточной Пруссии XVIII века Кенигсберге река, проходя через город, разветвлялась на две части, образуя посередине небольшой остров. Остров соединялся с частями города к северу, югу и востоку от него семью мостами. В какой-то момент у жителей Кенигсберга возник вопрос: существует ли способ передвижения по городу, при котором каждый из мостов пересекается один и только один раз? Когда этот игривый вопрос встретился со знаменитым математиком Леонгардом Эйлером, родилась теория графов.

Эйлер, эрудит, родившийся в Швейцарии, но живший в России, в 1736 году написал работу "Решение задачи о геометрии положения" (Solutio problematis ad geometriam situs pertinentis). В этой работе он дал однозначный ответ на вопрос: кёнигсбержец не может совершить прогулку по своему городу, проходя через каждый мост ровно один раз. Чтобы доказать это, ему пришлось упростить карту города до скелета ее полной структуры и работать с ней логически. Он показал, не используя слово, как превратить данные в граф и как выполнять на нем вычисления (см. рис. 20).

В контексте теории графов слово "граф" не означает график или диаграмму, как это принято в обычном языке. Скорее, граф - это математический объект, состоящий из узлов и ребер (в современном понимании).Узлы - это базовые единицы графа, а ребра представляют связи между ними. В примере с Кенигсбергом мосты служат ребрами, соединяющими четыре различных массива суши - узлы. Степень узла - это количество ребер, которые он имеет; таким образом, "степень" массива суши - 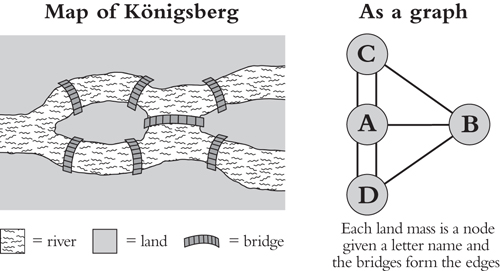это количество мостов, которые к нему подходят.

Рисунок 20

Эйлер подошел к вопросу о мостовых переходах, заметив, что путь через город можно записать в виде списка узлов. Если дать каждому массиву земли буквенное имя, то список "ABDC", например, будет представлять собой путь, который идет от острова в центре к земле внизу (через любой мост, соединяющий их), затем от него к массиву земли справа и далее к земле вверху. При таком пути через граф между каждой парой узлов проходит одно ребро. Таким образом, количество пересеченных мостов равно количеству букв в списке минус одна. Например, если вы пересекли два моста, то в вашем списке будет три земельных массива.

Затем Эйлер заметил нечто важное в количестве мостов, которые есть у каждого массива суши. Это число связано с тем, сколько раз этот массив должен появиться в списке путей. Например, у массива земли B есть три моста, а значит, "B" должен дважды появиться в любом пути, который пересекает каждый мост по одному разу - то есть нет способа пересечь эти три моста, не посетив B дважды. То же самое верно и для массивов C и D, поскольку у них тоже по два моста. А вот массив A с пятью мостами должен появиться в списке путей три раза.

Вместе взятые, любой путь, удовлетворяющий этим требованиям, будет состоять из девяти (2+2+2+3) букв. Однако список из девяти букв представляет собой путь, пересекающий восемь мостов. Поэтому невозможно построить путь, который пересекает каждый из семи мостов только один раз.

Используя эту зависимость между степенью узла и количеством раз, которое этот узел должен встретиться на пути, Эйлер вывел ряд общих правил о том, какие пути возможны. Теперь он мог сказать для любого набора мостов, соединяющих любые участки земли, существует ли путь, пересекающий каждый мост только один раз.

Более того, неважно, говорим ли мы вообще о земле и мостах. Та же процедура может быть использована для поиска путей для городского снегоуборщика, который должен очистить каждую улицу только один раз, или для того, чтобы узнать, можно ли обойти Википедию, нажимая на каждую гиперссылку между сайтами только один раз. Эта податливость - часть того, что придает теории графов ее силу. Отбрасывая детали любой конкретной ситуации, она находит структуру, которая похожа на все остальные. Этот абстрактный и чуждый способ взглянуть на проблему может открыть ее для новых и инновационных решений, подобно тому как Эйлеру помогло рассмотрение прогулки по городу как списка писем.