За десятилетия, предшествовавшие работе Лапика, понимание мембран, окружающих клетки, расширилось. Становилось ясно, что эти пучки биологических молекул работают как кирпичная стена: они мало что пропускают. Среди частиц, которые они способны удерживать, были ионы - атомы различных элементов, таких как хлорид, натрий или калий, которые несут положительный или отрицательный заряд. Таким образом, как заряженные частицы могли накапливаться по обе стороны стекла лейденской банки, так же они могли накапливаться внутри и снаружи клетки. Как писал Лапик в своей работе 1907 года: "Эти идеи приводят, при самом простом подходе, к уже установленным уравнениям для поляризации металлических электродов".
Таким образом, он пришел к описанию нерва в терминах "эквивалентной схемы".(см. рис. 2) То есть он предположил,что различные части нерва действуют подобно различным компонентам электрической цепи. Первая эквивалентность была установлена между клеточной мембраной и конденсатором, поскольку мембрана могла накапливать заряд точно таким же образом. Но было ясно, что эти мембраны не действуют как идеальные конденсаторы: они не могут удерживать весь заряд. Вместо этого между внутренней и внешней частью клетки протекал ток, который позволял ей немного разряжаться. Эту роль могла бы сыграть проволока с некоторым сопротивлением. Поэтому Лапик добавил в модель нерва резистор параллельно конденсатору. Таким образом, когда в цепь подается ток, часть заряда попадает на конденсатор, а часть проходит через резистор. Поэтому пытаться создать разность зарядов в клетке - все равно что наливать воду в неидеальное ведро: большая часть ее останется в ведре, а часть вытечет.
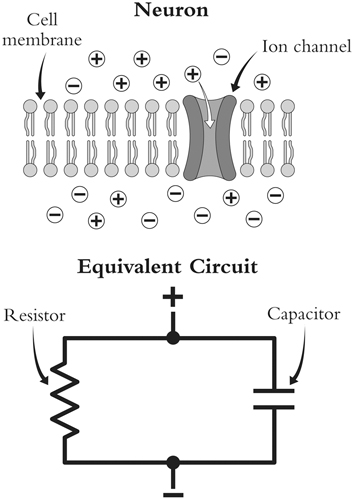
Рисунок 2
Эта аналогия между клеткой и электрической цепью позволила Лапику записать уравнение.Уравнение описывало, какдолжно менятьсянапряжение намембранеклеткис течением времени, в зависимости от того, какое напряжение к ней прикладывается и как долго. С помощью этой формализации он мог рассчитать, когда нерв отреагирует.
Чтобы проверить свое уравнение на данных, Лапик обратился к стандартному эксперименту с лягушачьей лапкой: он подавал на нерв лягушки напряжение разной величины и фиксировал время, необходимое для появления реакции. Лапик предположил, что когда нерв лягушки реагирует, это происходит потому, что напряжение на его мембране достигло определенного порога. Поэтому он рассчитал, сколько времени потребуется его модели для достижения этого порога при каждом разном напряжении. Сравнив предсказания своей модели с результатами экспериментов, Лапик обнаружил хорошее совпадение. Он мог предсказать, как долго нужно подавать определенное напряжение, чтобы нерв отреагировал.
Лапик был не первым, кто записал такое уравнение. Предыдущий ученый, Жорж Вейс, предложил свою догадку о том, как описать эту зависимость между напряжением и временем. И это была относительно хорошая догадка: она лишь немного отклонялась от предсказаний Лапика, например, в случае напряжения, приложенного в течение длительного времени. Но подобно тому, как малейшая улика на месте преступления может изменить картину всего события, это небольшое расхождение между предсказаниями уравнения Лапика и тем, что было до него, на самом деле означало глубокое расхождение в понимании.
В отличие от уравнения Лапика, уравнение Вайса не было вдохновлено механикой клетки и не предназначалось для интерпретации в качестве эквивалентной схемы. Это было скорее описание данных, чем их модель. Если описательное уравнение - это, как мультипликационная анимация события - фиксирует его внешний вид, но без глубины, то модель - это повторное воспроизведение. Таким образом, математическая модель нервного импульса должна иметь те же подвижные части, что и сам нерв. Каждая переменная должна быть сопоставима с реальным физическим объектом, а их взаимодействие должно отражать реальный мир. Именно это и обеспечила эквивалентная схема Лапика: уравнение, в котором термины можно интерпретировать.
Еще до Лапика другие исследователи заметили сходство между электрическими инструментами, используемыми для изучения нерва, и самим нервом. Лапик в значительной степени опирался на работы Вальтера Нернста, который заметил, что способность мембраны разделять ионы может лежать в основе потенциала действия. Другой ученик дю Буа-Реймона, Людимар Герман, говорил о нерве в терминах конденсаторов и резисторов. И даже сам Гальвани представлял себе нерв, работающий аналогично его лейденской банке. Но Лапик с его явной эквивалентной схемой и количественным соответствием данным сделал еще один шаг вперед в аргументации в пользу нерва как точного электрического устройства. Как он писал: "Физическая интерпретация, к которой я пришел сегодня, придает точный смысл нескольким важным ранее известным фактам о возбудимости... Мне кажется, это повод считать ее шагом в направлении реализма".
Из-за ограниченного оборудования большинство нейробиологов того времени записывали данные с целых нервов. Нервы представляют собой пучки аксонов - волокон, по которым отдельные нейроны передают сигналы другим клеткам. Записывая сразу множество аксонов, легче уловить изменения тока, которые они производят, но сложнее увидеть детальную форму этих изменений. Однако, вставляя электрод в один нейрон, можнонапрямую регистрировать напряжение на его мембране. Как только в начале XX века появилась технология наблюдения за отдельными нейронами, потенциал действия стал гораздо более понятным.
Одна из определяющих особенностей потенциала действия, замеченная английским физиологом Эдгаром Адрианом в 1920-х годах, - принцип "все или ничего". Принцип "все или ничего" гласит, что нейрон либо испускает потенциал действия, либо нет - ничего промежуточного. Другими словами, каждый раз, когда нейрон получает достаточно входного сигнала, напряжение на его мембране меняется - и меняется абсолютно одинаково. Поэтому, как гол в хоккее считается одинаково, независимо от того, с какой силой шайба забита в сетку, так и сильная стимуляция нейрона не делает его потенциал действия больше или лучше. Все, что может сделать сильная стимуляция, - это заставить нейрон излучать больше точно таких же потенциалов действия. Таким образом, нервная система больше заботится о количестве, чем о качестве.
Природа нейрона "все или ничего" согласуется с интуицией Лапика о пороге. Он знал, что напряжение на мембране должно достичь определенного значения, чтобы нерв отреагировал. Но как только оно достигало этого значения, ответ был ответом.
К 1960-м годам принцип "все или ничего" был объединен с уравнением Лапика в математическую модель, известную как "нейрон с утечкой и огнем" (leaky integrate-and-fire neuron):"утечка" - потому что наличие резистора означает утечку части тока; "интеграция" - потому что конденсатор интегрирует оставшуюся часть тока и сохраняет ее в виде заряда; и "огонь" - потому что, когда напряжение на конденсаторе достигает порога, нейрон "выстреливает", или излучает потенциал действия. После каждого "выстрела" напряжение возвращается к исходному уровню, чтобы снова достичь порога, если на нейрон подается больше входного сигнала.
Несмотря на простоту модели, она может воспроизводить особенности работы реальных нейронов: например, при сильном и постоянном входном сигнале нейрон модели будет многократно запускать потенциалы действия с небольшой задержкой между каждым из них; если же входной сигнал достаточно слабый, он может оставаться включенным бесконечно долго, не вызывая ни одного потенциала действия.
Эти модельные нейроны можно также заставить образовывать связи - соединяться друг с другом таким образом, чтобы возбуждение одного из них генерировало входной сигнал для другого. Это дает моделистам более широкие возможности: воспроизводить, изучать и понимать поведение не только отдельных нейронов, но и целых сетей.
С момента своего появления такие модели использовались для изучения множества аспектов работы мозга, включая болезни. Болезнь Паркинсона - это заболевание, при котором нарушается работа нейронов в базальных ганглиях. Расположенные глубоко в мозге, базальные ганглии состоят из множества областей с замысловатыми латинскими названиями. Когда при болезни Паркинсона нарушается питание одной из областей - стриатума, это выводит из равновесия остальные базальные ганглии. В результате изменений в стриатуме субталамическое ядро (еще одна область базальных ганглиев) начинает активнее работать, что вызывает возбуждение нейронов во внешнем глобусе паллидуса (еще одна область базальных ганглиев). Но эти нейроны посылают связи обратно в субталамическое ядро, котороене дает этим нейронам разгореться еще больше, что, в свою очередь, отключает и сам внешний паллидус глобуса. Результатом этой сложной сети связей являются осцилляции: нейроны в этой сети стреляют больше, потом меньше, потом снова больше. Эти ритмы, по-видимому, связаны с двигательными проблемами пациентов с болезнью Паркинсона - тремором, замедленными движениями и ригидностью.
В 2011 году исследователи из Фрайбургского университета построили компьютерную модель этих областей мозга, состоящую из 3 000 негерметичных интегративных и огневых нейронов. В модели нарушение работы клеток, представляющих стриатум, вызывало те же проблемные волны активности, которые наблюдаются в субталамических ядрах у пациентов с болезнью Паркинсона. Модель, демонстрирующая признаки заболевания, может быть использована для изучения способов его лечения. Например, введение импульсов входного сигнала в субталамическое ядро модели разрушало эти волны и восстанавливало нормальную активность. Но импульсы должны были быть в правильном темпе - слишком медленные колебания ухудшались, а не улучшались. Глубокая стимуляция мозга - процедура, при которой импульсы электрической активности вводятся в субталамическое ядро пациентов с болезнью Паркинсона, - как известно, помогает облегчить тремор. Врачи, использующие этот метод лечения, также знают, что частота импульсов должна быть высокой - около 100 раз в секунду. Эта модель дает подсказку, почему высокая частота стимуляции работает лучше, чем низкая. Таким образом, моделирование мозга как серии взаимосвязанных цепей позволяет понять, как применение электричества может регулировать его работу.