Высота дерева
Узнать высоту предмета с помощью собственной тени можно только в солнечный день. С древних времен геометрия создала много других способов измерения высоты предметов.
Расскажу о некоторых из них.
Во время Великой Отечественной войны командиру отдельного саперного батальона было приказано срочно построить мост через речку. Он вызвал к себе сержанта и приказал ему узнать высоту деревьев в ближайшем лесу.
Сержант воткнул шест длиной около 2,5 метра на некотором расстоянии от измеряемого дерева, надрезал на шесте черточку на высоте глаза, затем отошел от шеста и стал в такой точке, чтобы конец шеста закрывал собой макушку дерева.

Как видно из рисунка, получились два подобных прямоугольных треугольника, и можно написать такую пропорцию:
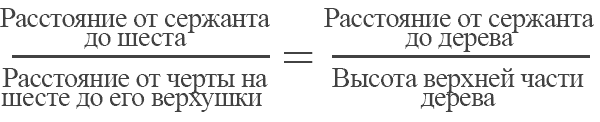
Первые три величины (расстояние до шеста, расстояние от черты на шесте до его верхушки, расстояние до дерева) сержант измерил рулеткой, а по ним узнал четвертую, прибавил к ней высоту своего глаза над землей — и получил высоту измеряемого дерева.
Вот еще один очень несложный способ.
У вас есть линейка с миллиметровыми делениями. Это и будет ваш высотомер.
Станьте где-нибудь в стороне от дерева, вытяните руку и держите линейку вертикально.
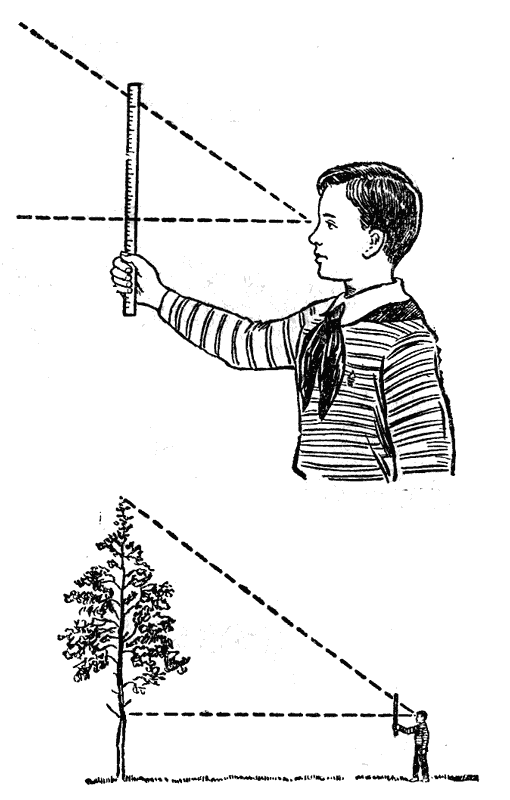
Ноль линейки направьте на самый низ дерева и одновременно посмотрите, какая цифра на линейке совместится с его макушкой.
Опять получились подобные, но не прямоугольные, а равнобедренные треугольники, из которых можно составить такую пропорцию:

Вы знаете, что первый размер равен 0,6 метра, отсчет по линейке вы уже взяли, расстояние от глаза до дерева вы измерите[13]. По этим трем величинам вы узнаете четвертую — высоту дерева.
Наконец, можно измерить высоту дерева с помощью крестовины вашего эккера. Возьмите ее в руки вертикально и станьте в такой точке, чтобы один створ булавок — № 1 и № 3 — был направлен на черту на дереве, замеченную на высоте вашего глаза, а другой створ булавок — № 1 и № 2 — под углом 45° на макушку дерева.
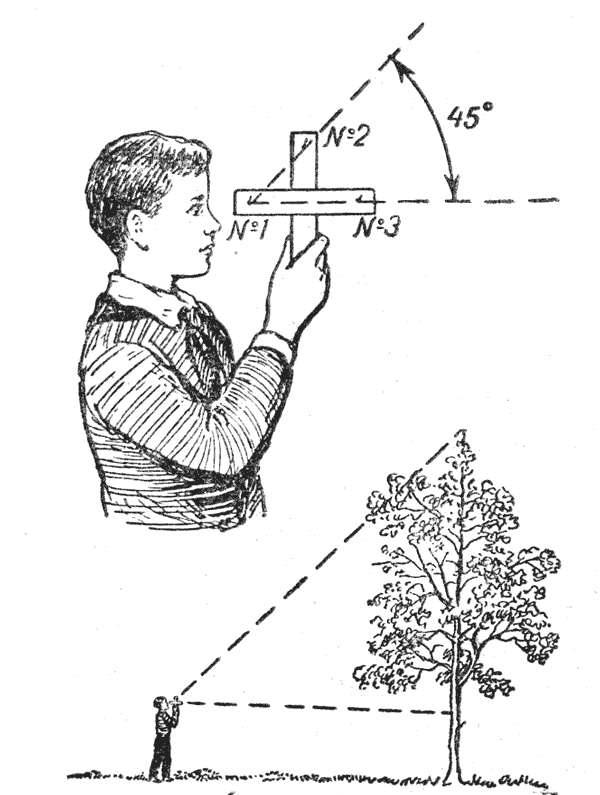
Как видите, у вас получился равнобедренный прямоугольный треугольник, и, следовательно, высота дерева равна расстоянию от вас до дерева плюс ваш рост до глаз.
Во всех описанных случаях предполагается, что и дерево и наблюдатель находятся на одной горизонтальной плоскости.