Рис. 7

Находим значения функции в точках экстремума: y(3) = 108, y(5) = 0. График функции показан на рис. 8.

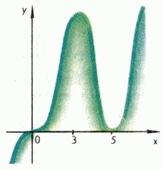
Рис. 8

Заметим, что возможны случаи, когда экстремум достигается в точке, в которой производная не существует. Таковы точки экстремума у профиля пилы, пример такой функции дан и на рис. 1.

Задачи на максимум и минимум имеют важнейшее значение в физике, механике, различных приложениях математики. Они были теми задачами, которые привели математику к созданию дифференциального исчисления, а дифференциальное исчисление дало мощный общий метод решения задач на экстремум с помощью производной.

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ

Основными элементарными функциями считаются: многочлен, рациональная функция, которая представляет собой отношение двух многочленов, степенная функция, показательная функция, логарифмическая функция, тригонометрические функции и обратные тригонометрические функции.

К элементарным функциям относятся и те функции, которые получаются из элементарных путем применения (конечного числа раз) основных четырех арифметических действий и образования сложной функции. Приведем несколько примеров элементарных функций:

, f₂(x) = cos lg x, f₃(x) = x2^x + arctg x,

, f₅ = x^{sin x} - sin tg x.

Отметим, что функция f(x) = |x| также является элементарной, поскольку |x| = √x².

Элементарные функции наиболее изучены и часто используются в приложениях математики.

Хотя понятие функции сформировалось лишь в XVII в., однако зависимости между двумя величинами рассматривались и ранее. К XVII в. почти все основные элементарные функции были достаточно хорошо изучены: к этому времени уже были составлены высокой точности таблицы значений тригонометрических функций и появились первые таблицы логарифмов. Дифференциальное исчисление дало законченное исследование основных элементарных функций, в частности было установлено, что производная от элементарной функции есть также элементарная функция.

Развитие математического анализа, решение различных прикладных задач привели к рассмотрению функций, которые не являются элементарными. Например, не выражаются через элементарные функции решения дифференциальных уравнений:

y^t = e^x /x,

.

При изучении неэлементарных функций их, как правило, выражают через элементарные с помощью пределов, интегралов, бесконечных рядов и исследуют методами математического анализа.

ЭЛЛИПС

Эллипс - одно из конических сечений. Его также можно определить как фигуру, состоящую из всех тех точек плоскости, сумма расстояний от которых до двух заданных точек F₁ и F₂ (называемых фокусами эллипса) является постоянной величиной, обычно обозначаемой через 2a (рис. 1).

Рис. 1

Из этого определения нетрудно установить, что прямая, проходящая через фокусы эллипса, есть его ось симметрии, как и прямая, являющаяся серединным перпендикуляром отрезка F₁F₂. Точка O пересечения этих прямых служит центром симметрии эллипса, его называют просто центром эллипса. Если взять указанные прямые в качестве осей координат, то уравнение эллипса запишется в виде x²/a² + y²/b² = 1.

Из уравнения эллипса следует, что ось абсцисс эллипс пересекает в точках (a,0) и (-a,0), а ось ординат - в точках (b,0) и (-b,0). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами на оси абсцисс называется большой осью, а на оси ординат - малой осью. Их отрезки от вершины до центра эллипса называются полуосями.

Зная определение эллипса, можно сделать простейший прибор, вычерчивающий эллипс. Для этого надо связать две булавки ниткой и воткнуть их в чертежную доску (рис. 2), взять карандаш и двигать его по бумаге так, чтобы грифель карандаша все время натягивал нитку. Тогда кончик грифеля будет рисовать на бумаге эллипс.

Рис. 2

А как получить эллипс с данными полуосями a и b? Оказывается, не случайно сумма расстояний от фокусов до точки на эллипсе обозначена через 2a. Эта сумма равна длине большой оси. Укрепленные на доске булавки задали расстояние между фокусами, его обычно обозначают через 2c, таким образом, c - расстояние от центра эллипса до его фокуса. Если рассмотреть теперь прямоугольный треугольник OAF₂ на рис. 1, то из него видно, что a² = b² + c². Таким образом, если известны величины полуосей эллипса, то расстояние от его центра до каждого из фокусов будет катетом прямоугольного треугольника с гипотенузой, равной большой полуоси, и вторым катетом, равным малой полуоси. Итак, все нужные величины имеются, и можно построить искомый эллипс. Этот способ часто используют садовники при разбивке клумб.

Второй способ построения эллипса основан на том факте, что при сжатии окружности к ее диаметру получается эллипс. Способ построения точек эллипса с полуосями a и b ясен из рис. 3, где внешняя и внутренняя окружности имеют радиусы соответственно a и b.

Рис. 3

Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее вытянут эллипс вдоль большой оси. Однако степень вытянутости эллипса принято выражать через другой параметр, общий для всех конических сечений, - эксцентриситет ε, который в данном случае лучше определить как отношение расстояния от центра до фокуса к длине большой полуоси (ε = c/a). Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы. У планет, которые, как известно, движутся по эллипсам, самый маленький эксцентриситет имеет орбита Венеры (0,0068), следующий по величине эксцентриситет у Нептуна (0,0086), затем у Земли (0,0167). Самый большой эксцентриситет у Плутона (0,253), однако он не идет ни в какое сравнение с эксцентриситетами комет. Так, комета Галлея имеет эксцентриситет 0,967.

Тот факт, что эллипс является результатом сжатия окружности, объясняет, почему круглые предметы: колеса машин, иллюминаторы кораблей, циферблаты часов и т.д. - мы видим как эллипсы, если смотрим на них под углом.

Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с фокусами, пересекают касательную к эллипсу в этой точке под разными углами. А это значит, что луч, пущенный из одного фокуса, после отражения попадет в другой (рис. 1). Это свойство лежит в основе интересного акустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико (рис. 4).

Рис. 4

Рассмотрим поверхность, полученную в результате вращения эллипса вокруг одной из его осей. Такая поверхность называется эллипсоидом вращения. Если вращать эллипс вокруг большой оси, то получится яйцеобразная фигура (рис. 5,а). Если вращать его вокруг малой оси, то полученная поверхность - сплюснутая сфера (рис. 5,б). Заметим, что Земля имеет такую форму, поскольку расстояние между ее полюсами (12 714 км) меньше, чем расстояние между диаметрально противоположными точками экватора (12 756 км).