С развитием алгебры, уже при решении линейных уравнений с одним неизвестным, возникает необходимость в отрицательных числах. Еще до нашей эры их стали употреблять китайские математики. Широко использовали отрицательные числа и индийские математики (Брахмагупта, VII в.). Замечательным достижением индийских математиков было введение понятия нуля и знака для него, что позволило им создать десятичную систему записи натуральных чисел и разработать правила операций над записанными так числами. Эту запись чисел стали применять математики многих восточных стран, откуда она попала в Европу.
В XV в. самаркандский ученый ал-Каши ввел десятичные дроби. Это нововведение оставалось неизвестным европейским математикам, и лишь в 1584 г. нидерландский математик и инженер С. Стевин вновь пришел к этому открытию. Числа целые, дробные (положительные и отрицательные) и нуль получили общее название рациональных чисел.
Следующими важными этапами в развитии понятия числа были открытие комплексных чисел и формальное построение теории действительных чисел на основе понятия натурального числа.
Изучение понятия числа шло не только путем обобщения, но и путем выделения из общего понятия числа важных частных случаев. Например, в множестве R действительных чисел были выделены рациональные и иррациональные числа, т.е. числа, которые соответственно можно записать в виде дроби p/q и которые нельзя записать в таком виде. По своей десятичной записи эти виды чисел различаются тем, что в записи рационального числа, начиная с некоторого места, неизменно повторяется одна и та же цифра или группа цифр, тогда как в записи иррационального числа такого повторения наступить не может. Так, 0,333...(=1/34), 5,0323232...(=2491/495) - рациональные числа; 1,4142...(=√2), 3,14159...(=π) - иррациональные числа.
Далее были выделены алгебраические числа, т.е. числа, являющиеся корнями уравнений вида
a0xn+a1xn-1+...+an,
где a0,a1,an - целые числа (если, кроме того, a0 = 1, то корень уравнения называют целым алгебраическим числом). Примерами алгебраических чисел могут служить 1 + √2 (корень уравнения x2-2x-1=0),
Все числа, не являющиеся алгебраическими, называют трансцендентными. Очевидно, что все трансцендентные числа иррациональны. Трансцендентно число π=3,1415926..., играющее важнейшую роль в математике. Отсюда вытекает, в частности, невозможность «квадратуры круга» (см. Классические задачи древности). Трансцендентно и число
ЭКСТРЕМУМ ФУНКЦИИ
Рассмотрим два зубца хорошо всем известного профиля пилы. Направим ось Ox вдоль ровной стороны пилы, а ось Oy - перпендикулярно к ней. Получим график некоторой функции, изображенный на рис. 1.

Рис. 1
Совершенно очевидно, что и в точке a1, и в точке a2 значения функции оказываются наибольшими в сравнении со значениями в соседних точках справа и слева, а в точке b2 - наименьшим в сравнении с соседними точками. Точки a1,a2,b2 называются точками экстремума функции (от латинского extremum - «крайний»), точки a1 и a2 - точками максимума, а точка b2 - точкой минимума (от латинских maximum и minimum - «наибольший» и «наименьший»).
Уточним определение экстремума.
Говорят, что функция f(x) в точке x0 имеет максимум, если найдется интервал, содержащий точку x0 и принадлежащий области определения функции, такой, что для всех точек x этого интервала оказывается f(x) < f(x0). Соответственно функция f(x) в точке x0 имеет минимум, если для всех точек некоторого интервала выполняется условие f(x) > f(x0).
На рис. 2 и 3 приведены графики функций, имеющие в точке x=0 экстремум.

Рис. 2
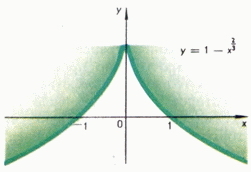
Рис. 3
Обратим внимание на то, что по определению точка экстремума должна лежать внутри промежутка задания функции, а не на его конце. Поэтому для функции, изображенной на рис. 1, нельзя считать, что в точке b1 она имеет минимум.
Если в данном определении максимума (минимума) функции заменить строгое неравенство на нестрогое f(x) ≤ f(x0) (f(x) ≥ f(x0)), то получим определение нестрогого максимума (нестрогого минимума). Рассмотрим для примера профиль вершины горы (рис. 4). Каждая точка x плоской площадки - отрезка [x1,x2] является точкой нестрогого максимума.

Рис. 4
В дифференциальном исчислении исследование функции на экстремумы очень эффективно и достаточно просто осуществляется с помощью производной. Одна из основных теорем дифференциального исчисления, устанавливающая необходимое условие экстремума дифференцируемой функции, - теорема Ферма (см. Ферма теорема). Пусть функция f(x) в точке x0 имеет экстремум. Если в этой точке существует производная f'(x0), то она равна нулю.
На геометрическом языке теорема Ферма означает, что в точке экстремума касательная к графику функции горизонтальна (рис. 5). Обратное утверждение, разумеется, неверно, что показывает, например, график на рис. 6.

Рис. 5

Рис. 6
Теорема названа в честь французского математика П. Ферма, который одним из первых решил ряд задач на экстремум. Он еще не располагал понятием производной, но применял при исследовании метод, сущность которого выражена в утверждении теоремы.
Достаточным условием экстремума дифференцируемой функции является смена знака производной. Если в точке x0 производная меняет знак с минуса на плюс, т.е. ее убывание сменяется возрастанием, то точка x0 будет точкой минимума. Напротив, точка x0 будет точкой максимума, если производная меняет знак с плюса на минус, т.е. переходит от возрастания к убыванию.
Точка, где производная функции равна нулю, называется стационарной. Если исследуется на экстремум дифференцируемая функция, то следует найти все ее стационарные точки и рассмотреть знаки производной слева и справа от них.
Исследуем на экстремум функцию y = x3(x - 5)2.
Найдем ее производную: y' = 5x2(x-5)(x-3).
Определяем стационарные точки: x1 = 0, x2 = 3, x3 = 5. Нетрудно заметить, что в интервалах между стационарными точками знак производной не изменяется, на каждом из интервалов он отмечен на рис. 7. Используя достаточное условие экстремума, можно сделать заключение: в точке x1 = 0 экстремума нет; точка x2 = 3 - точка максимума; точка x3 = 5 - точка минимума.