Зная, как определять направление магнитного поля, а также правила нахождения направления силы, действующей на ток со стороны магнитного поля (о чем чуть ниже), читатель сумеет сам выяснить, что параллельно текущие токи притягиваются, противоположно направленные отталкиваются.

Однородным является такое магнитное поле, действие которого на любые индикаторы поля одинаково в разных местах.

Такое поле удается создать между полюсами магнита. Естественно, чем ближе друг к другу расположены полюса и чем больше плоская поверхность торцов магнита, тем поле однороднее.

О действии однородного магнитного поля на магнитную стрелку и контур тока уже сказано: если нет уравновешивающей пружины, то они установятся в поле так, чтобы их магнитный момент совпадал с направлением поля. «Северный полюс» будет смотреть на «южный полюс» магнита. Этот же факт можно выразить словами: магнитный момент установится вдоль силовых линий магнитного поля.

Рассмотрим теперь действие магнитного поля на движущиеся заряды.

В том, что действие имеется, и притом весьма немалое, убедиться донельзя просто: достаточно поднести самый обычный школьный магнит к электронному лучу, созданному электронной пушкой. Светящееся пятно на экране сместится и будет менять место на экране в зависимости от положения магнита.

От качественной демонстрации явления можно перейти к количественному исследованию, и тогда окажется, что величина силы, действующей со стороны магнитного поля В на электрон, движущийся в поле со скоростью v под прямым углом к силовым линиям, равна

F = e∙v∙B,

где е заряд частицы (закон, конечно, справедлив не только для электронов, но и для любых заряженных частиц).

А вот если частица движется вдоль силовой линии магнитного <поля, то поле на нее не действует! Читателю, знающему тригонометрию, нетрудно сообразить, как написать выражение силы для случая движения под некоторым углом к полю. Мы не станем загромождать текст формулами, которые нам не понадобятся в дальнейшем.

Но еще ничего не сказано о направлении силы. А это крайне важно. Опыт показывает, что сила перпендикулярна как направлению движения частицы, так и направлению индукции. Или иначе: перпендикулярна плоскости, проходящей через вектора v и В. Но этим ведь еще не все сказано. У каждой медали две стороны. В чем они отличны? В направлении поворота, совмещающего один вектор с другим. Если поворот вектора и к вектору В на угол, меньший 180°, мы видим происходящим против часовой стрелки, то эту сторону называют положительной.

Простые векторные схемы, изображенные слева на рис. 3.3, показывают, что положительно заряженная частица отклоняется в сторону положительной нормали. Электрон отклоняется в обратную сторону.

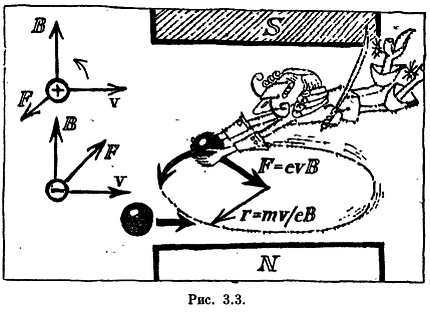
Теперь поглядите, к какому интересному результату приводит этот закон для электрона, влетевшего в постоянное магнитное поле под прямым углом (рис. 3.3 справа). Сообразите: какую траекторию будет описывать электрон? Ну, конечно, он будет двигаться по окружности. Сила магнитного поля является центростремительной силой, и мы сразу же вычислим радиус окружности, приравнивая m∙v²/r и е∙v∙В. Итак, радиус траектории равен.

r = m∙v/e∙B.

Обратите внимание на то, что по поведению частицы вы можете вычислить ее свойства. Но опять та же история, с которой мы столкнулись, изучая движения частицы в электрическом поле. Не удается определить отдельно электрический заряд и отдельно массу частицы!

Опыт приводит нас и в этом случае к величине отношения e/m.

Итак, частица движется по окружности, если ее скорость направлена под прямым углом к магнитному полю; частица движется по инерции, если ее скорость направлена вдоль магнитного поля. Ну, а в общем случае? Ваш ответ, конечно, уже готов. Частица движется по спирали, осью которой является силовая линия. Спираль будет состоять из тесно или редко навитых витков, в зависимости от начального угла влета электрона в магнитное поле.

Раз магнитное поле действует на движущуюся частицу, то оно должно оказывать силу и на каждый кусочек провода, по которому течет ток. Рассмотрим «отрезок» электронного луча длиной l. Пусть на этом отрезке умещается n частиц. Сила, действующая на провод такой же длины, по которому движется столько же частиц с такой же скоростью, будет равна n∙e∙v∙B. Сила тока равняется полному заряду, проходящему через провод в единицу времени. Время τ, за которое рассматриваемые электроны пробегут путь l, равно

τ = l/v

То есть силу тока можно записать так:

I = n∙e/τ

Подставляя скорость

v = I∙l/n∙e

из этого выражения в формулу для силы, действующей на «отрезок» электронного луча, мы и найдем силу, которая действует на проводник длиной l. Вот это выражение:

F = I∙l∙В.

Оно справедливо только для случая, когда провод перпендикулярен полю.

Направление отклонения провода, по которому протекает ток, можно определить с помощью схемы, показанной на рис. 3.3.

Из уважения к исследователям, работавшим в девятнадцатом веке, я привожу рис. 3.4.

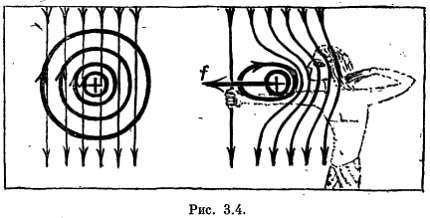
Впрочем, рисунок представляет не только академический интерес. Он помогает запомнить правило отклонения токов. Рисунок показывает, как сложится собственное поле тока (идущего «от нас») с внешним полем. Результат сложения показан справа. Если представлять себе силовые линии как натяжения эфирной материи (а такая точка зрения была широко распространена в прошлом веке), то направление смещения проводника получает наглядную интерпретаций: проводник просто выталкивается полем.

Покажем теперь, что действие магнитного поля на движущийся заряд и на отрезок тока — это то же самое явление, с которого мы начали рассмотрение действий магнитного поля.

Вернемся к рис. 3.1. На рисунке показаны силы, действующие на контур тока. На участки провода, идущие вдоль силовых линий, силы не действуют, на другие два участка действует пара сил, и из рисунка ясно, что момент этой пары как раз и равен произведению силы на плечо:

N = I∙l∙B∙d = I∙S∙В = M∙B.

Таким образом, выражение для момента силы как произведения магнитного момента контура на величину магнитной индукции прямо вытекает из формулы силы, действующей на заряд.

Кстати говоря, формула F = e∙v∙B, с которой мы начали этот параграф, носит имя Лоренца (Гендрик Антон Лоренц, 1853–1928, голландский физик, предложил эту формулу в 1895 г.).

Создать неоднородное магнитное поле совсем нетрудно. Скажем, можно полюсам магнита придать изогнутую форму (рис. 3.5). Тогда ход силовых линий будет таким, как показано на рисунке.

Положим, что полюса достаточно отдалены друг от друга, и поместим магнитную стрелку вблизи одного из полюсов. Как мы бегло упомянули, в общем случае магнитная стрелка не только поворачивается, но и движется поступательно. Одно лишь вращательное движение магнитной стрелки (или контура тока) наблюдается в том случае, если поле однородно. А вот в неоднородном поле будут иметь место оба движения. Стрелка повернется так, чтобы установиться вдоль силовых линий, а далее она начнет притягиваться к полюсу (см. рис. 3.5). Стрелка втягивается в ту область, где поле сильнее. (Конечно, художник перестарался — вряд ли даже сильное поле разломает компас.)