— Вот кусочек гиперболической площади, — сказал он. — Так?

— 366 —

Затем Радикс осторожно передвинул резиновую перегородочку от абсциссы «1» до абсциссы «3».

Илюша внимательно посмотрел и увидел, что теперь поверхность ртути оказалась сверху против точки с абсциссой х = 6.

— Понятно? — спросил Радикс.

— Из одного трапецоида вышло три, — задумчиво констатировал мальчик. — Было от одного до двух, а теперь стало от трех до шести. А как это получилось, не знаю,…

Радикс махнул ручонкой, и вся ртуть немедленно исчезла.

Поглядев машинально на банку, Илюша заметил, что количество ртути в банке снова увеличилось, а сбоку прыгает одна капелька, никак не может попасть обратно в банку.

Вот как Радикс сначала поставил этот чертеж

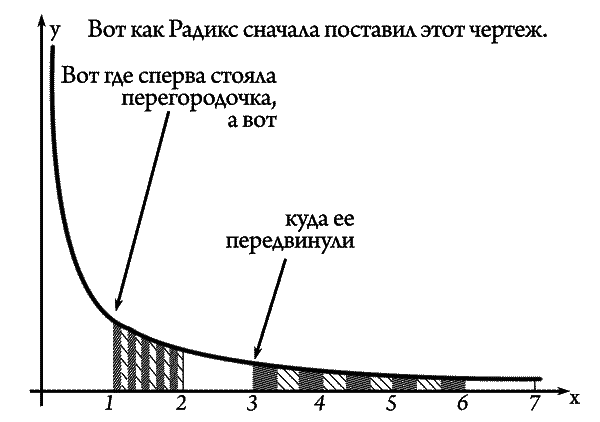
А потом повернули обратно

— Возьмем, — сказал Радикс, — очень тонкую полоску, толщиной в долю микрона. Если взять еще тоньше, так, пожалуй, и не увидишь. Так ведь и делали математики в старое время, когда свойства бесконечно малых не были еще достаточно хорошо исследованы и обсуждены. В этом роде действовали, например, Архимед, Кеплер и Кавальери. Это было начало возникновения анализа бесконечно малых, и при разрешении некоторых, сравнительно простых вопросов в руках крупных ученых этот несовершенный способ давал серьезные, а для тех времен даже и решающие результаты. Во всяком случае, без

— 367 —

этих первых, робких и грубых попыток интегрировать и дифференцировать с помощью таких, как выражался Кавальерн, «неделимых» полосок вряд ли наука сумела бы создать то, чем стала математика в наше время. Итак, мы берем такую тончайшую полоску как раз против абсциссы с пометкой «один». Впрочем, сказать по совести, мне надоело возиться с перегородкой, и я привык, чтобы ось иксов шла горизонтально. Поэтому я попрошу ртуть теперь уж без подпорок занимать полагающееся ей пространство между двумя вертикальными ординатами гиперболы.

Оси послушно повернулись, а Радикс сердито глянул на банку со ртутью. Бедная капелька, которая никак не могла попасть обратно в банку, опрометью кинулась обратно к стеклянной гиперболе и немедленно растянулась против абсциссы «1» тоненькой-претоненькой блистающей серебряной ниточкой.

— Хороша «неделимая» полоска? — спросил Радикс.

— Да, — отвечал Илюша, — уж поистине «неделимая».

— Допустим! — усмехнулся Радикс. — Пусть на этот раз будет по-твоему. Это, конечно, не совсем по Кавальери… Ну, все равно, не будем уж на этот раз придираться!.. Но представь себе, что я хочу ее переместить к абсциссе с пометкой «три». Поскольку эта полоска имеет некоторую конечную толщину, хоть и очень небольшую, она, чтобы уместиться под гиперболой, должна стать короче, а самое главное — толще.

Так вот: во сколько раз она станет толще?

— Поскольку уравнение гиперболы дает для игрека величины, обратные иксу, то ясно, что для абсциссы «один» мы и ординату получаем «один», а для абсциссы «три» мы получаем «одну третью». Опираясь на уравнение гиперболы, я утверждаю, что наша полоска должна, если ее перенести от абсциссы «один» к абсциссе «три», стать толще в три раза, ибо одна треть в три раза меньше единицы. По-моему, иначе быть не может.

Немедленно тончайшая ртутная ниточка сложилась втрое и быстро двинулась направо. Действительно, когда она добралась до абсциссы «три», она стала той длины, какой в этом месте была ордината гиперболы.

— 368 —

— Ясно, — сказал Илюша.

— А далее, — спросил Радикс, — если взять еще одну тончайшую полоску, которая будет стоять рядом с первой, то с ней что будет?

— Я не могу сообразить сразу, как это будет, — отвечал мальчик, — но мне кажется, что если бы мы взяли целый полк тончайших полосок и стали их так перемещать…

Площадь.

— А ведь когда я перемещал целый трапецоид, я именно это и делал! — заметил Радикс.

— Ах да! — спохватился Илюша. — Разумеется. Но я уж буду пока по-своему рассуждать. Итак, ты перемещаешь, скажем, две полоски, они стоят рядом… а стало быть, если первая, сложившись втрое, попадет в абсциссу «три», то ведь и вторая полоска очутится на расстоянии втрое более дальнем, а следовательно, и ей придется сложиться опять-таки втрое. А если это так, то очевидно, что и любая (то есть третья, четвертая, пятая и так далее) полоска тоже должна будет потолстеть при таком перемещении ровно втрое. А тогда и все они вместе, то есть вся площадь трапецоида, тоже должны будут стать втрое толще. И теперь понятно, почему ртуть заняла площадь от «трех» до «шести» по абсциссе.

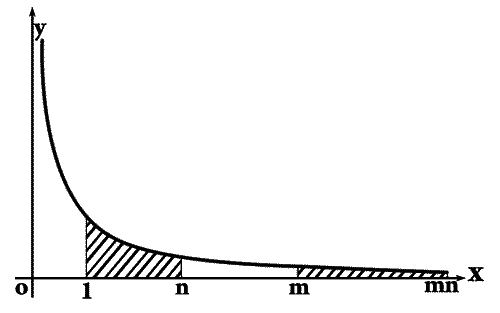
— Превосходно! — ответствовал Радикс.— Ну, а скажи мне, что будет, если я возьму площадку от икса, равного единице, до икса, равного некоторому n, и перенесу ее опять направо,

— 369 —

так, чтобы ее начало совпадало с иксом, равным какому-то m?

— Придется растянуть всю эту площадку в m раз. И она тогда займет расстояние по абсциссе от m до mn.

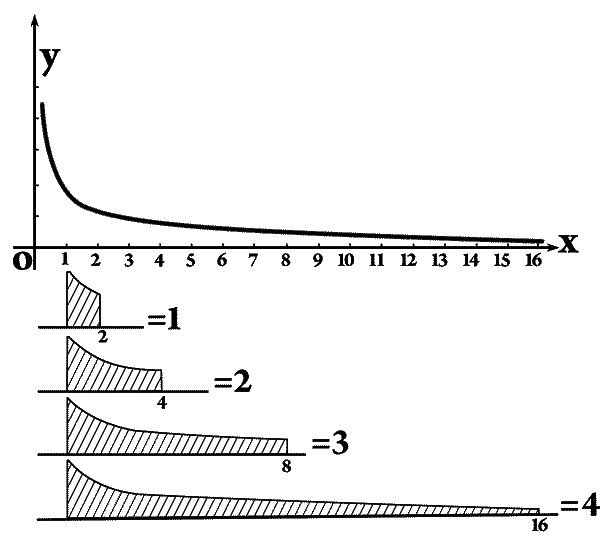
— Итак, — продолжал Радикс, — допустим теперь, что я возьму одну площадочку от «один» по абсциссе до «два». И теперь я хочу к ней пристроить сбоку, справа, еще одну точно такую же, то есть удвоить мою площадку. Затем, когда я пристрою вторую, я захочу пристроить третью, снова той же самой величины, то есть утроить первоначальную площадку. Затем пристрою четвертую, пятую и так далее. И все они должны быть равновеликими. Ну, что из этого получится?

Илюша задумался на минутку, а потом сказал так:

— А может, мне снова поможет наше рассуждение со ртутью? Если трапецоид перенести от абсциссы «один» к абсциссе «два», то ясно, что он растянется вдвое. Следовательно, и вторая пристраиваемая площадочка будет длинней по абсциссе, то есть продолжится от абсциссы «два» до абсциссы «четыре». Третья пристраиваемая площадка будет вдвое длиннее второй и займет место до абсциссы «восемь», а четвертая — вдвое длинней третьей, пятая — вдвое против четвертой и так далее. Значит, если начинать всегда от абсциссы «один» и брать первоначальную площадку, кончающуюся у абсциссы «два», то площадка, вдвое большая по площади, кончится у абсциссы «четыре», вчетверо большая по площади — у абсциссы «шестнадцать», впятеро большая — у абсциссы «тридцать два», и так далее, и так далее. Да ведь это выходит геометрическая прогрессия, раз каждая площадка вдвое длинней по абсциссе. Вот в чем дело! Площади в арифметической прогрессии, конечные абсциссы — в геометрической.

— Тебе ясно, какая у гиперболы связь с логарифмами?

— Да, — ответил Илюша.

— Если последовательно рассматривать абсциссы «два», «четыре», «восемь», «шестнадцать», «тридцать два»… идущие в геометрической прогрессии, и вычислять площади соответствующих гиперболических трапеций, начинающихся от абсциссы х = 1, причем единицей для измерения площадей будет площадь первой гиперболической трапеции от х = 1 до х = 2, то эти площади будут идти в арифметической прогрессии, то есть как показатели степеней числа «два», в которые надо возвести это основание, чтобы получить конечные абсциссы «два», «четыре», «восемь», «шестнадцать» и так далее. Поэтому можно сказать, что площадь каждой трапеции, измеренная указанным образом, будет равна логарифму конечной абсциссы при основании «два». Только мне не совсем понятно, почему мы взяли за единицу для измерения площадей именно эту первую гиперболическую площадку? Ведь за единицу для площадей принимают обыкновенно пло-

— 370 —

щадь квадрата со стороной, равной единице длины. Не проще ли и тут взять то же самое?

— Тогда как раз и получишь логарифмы, называемые натуральными, неперовыми, или гиперболическими. Ты можешь повторить все наше рассуждение, но только за начальную площадку придется выбрать гиперболическую трапецию, простирающуюся от абсциссы х = 1 на такое расстояние направо, насколько это нужно, чтобы под гиперболой получилась площадка, равновеликая квадрату со стороной «один». Ты заметишь по чертежу внизу, что такая начальная площадка должна доходить не до абсциссы х = 2, а немного дальше, приблизительно до 2,7. Эта конечная абсцисса обозначается буквой е и называется неперовым числом. Оно не менее знаменито, чем известное тебе число π. Если провести вычисление с большей точностью, то можно обнаружить, что