— 60 —
кроме того, что это фигура связная и что в ней нечетных узлов или совсем нет, или только два. Именно так следует поставить задачу общего математического доказательства.
— Я буду рассуждать так. Раз это фигура связная, то, значит, я имею возможность так или иначе из первого узла попасть в тот, где должно закончиться мое путешествие, то есть либо во второй нечетный узел, либо, если это фигура только с одними четными узлами, вернуться обратно в начальный узел. Чтобы не путаться, я самый простой такой маршрут отмечу красной линией, а остальные оставлю черными. А затем пойду по этой красной линии, но в каждом узле буду останавливаться и проверять, нет ли из него еще черных путей, которые надо обойти раньше, чем отправиться дальше по красному маршруту. Вот это и значит «идти правильно».
— Нет, — ответил Радикс, — это еще не всё. Почему ты так уверен, что можешь обойти каждую из твоих черных фигур?
— Потому что все узлы у них четные. И если в точках, через которые проходят и красные пути, не считать этих красных путей, то для черных путей и эти узлы тоже будут четными…
— Справедливо! Но ведь таким образом мы приходим к той же самой задаче: снова надо доказать, что можно обойти эти фигуры. И вот мы подошли к самому важному пункту нашего рассуждения. Теперь будет не так трудно. Потому, что нам удалось привести задачу об обходе фигуры с некоторым данным числом путей к задаче об обходе фигуры с меньшим числом путей. Понимаешь?
— Понимаю! — воскликнул Илюша. — А эти новые, более простые задачи я опять сведу к таким же, но еще более простым… И так можно каждый раз уменьшать число путей, а ведь нам дано только некоторое определенное число путей…
— Будем говорить — конечное число путей.
— Хорошо. А так как нам дано конечное число путей, то в конце концов все они будут исчерпаны. А следовательно, я доказал, что всякую связную фигуру, у которой нечетных узлов или нет совсем, или их только два, можно обойти непрерывным движением, проходя по каждому пути только один раз, то есть, другими словами, что всякая такая фигура действительно уникурсальна. И при этом я нашел и общее правило такого обхода.
— Попробуй теперь изложить это правило коротко и ясно, то есть сформулировать его.
— Мы начинаем наше путешествие в одном из нечетных узлов, а если их нет, то в каком угодно. Потом наметим какой-
— 61 —
нибудь маршрут, который вернет нас в начальный узел или в случае двух нечетных узлов приведет во второй нечетный узел. Затем идем в обход, погашая в каждом узле тем же способом все те черные закоулки, которые не вошли в наш маршрут. Вот и всё.
— Хорошо, — отвечал Радикс. — А как ты полагаешь, надо ли заранее намечать маршрут или можно обойтись и без этого?
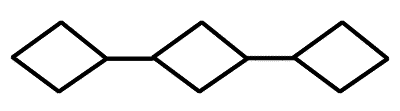
— Мне кажется, — начал Илюша, — что нельзя только упускать из виду того, что путь следует выбрать так, чтобы не нарушить связность фигуры. То есть я могу, например, при первой встрече с черным закоулком не обращать на него внимания, но надо обязательно обойти его из того узла, в котором я должен с ним расстаться. На чертеже (стр. 60) вот что получается: я могу пройти мимо черного закоулка — ромба CFGD, когда я дойду до узла С, но нельзя этого делать, когда я буду в узле D. Ну, разумеется, я говорю о том случае, когда мы двигаемся по направлению от В к Е.
— Так, — благосклонно отвечал Радикс, — все это верно. И, в общем, ты рассуждал довольно мило. Ну, а теперь уж тебе не так трудно будет доказать и еще один пункт, а именно: что всякое путешествие по уникурсальной фигуре, при котором ты, проходя через пути, не нарушаешь связности, приведет тебя к цели. Постарайся теперь это сформулировать?
— По-моему, это уже совсем просто. Мы идем вперед, не нарушая связности. Число путей у нас все время в силу этого уменьшается. Ясно, что в конце концов мы обойдем все пути.
— Точно, правильно, прекрасно! — задумчиво пробормотал Радикс. — А теперь вот что: дана фигура с несколькими нечетными узлами, и если их больше чем два, то она не уникурсальна.
Возникает вопрос: сколько надо сделать в таком случае обходов? Вот тебе фигура с четырьмя нечетными узлами.
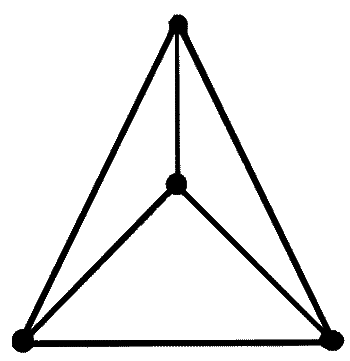
Фигура с четырьмя нечетными узлами.
Рассмотри, сколько надо сделать обходов. Ты увидишь, что обходов надо столько, сколько пар нечетных узлов имеется в фигуре. Это вполне естественно. Вот тебе еще задачка. Возьмем твой первый чертеж — два ромба, соединенных прямой (эту соединительную прямую в фигуре мы называем мостом). Теперь разорвем наш мост посредине. Подумай над таким вопросом: давай заполним разрыв моста какой-нибудь фигурой, то есть вставим в уникурсальную фигуру с двумя нечетными узлами еще одну связную фигуру, и разберемся, какую фигуру и как можно вставить. Только с четными узлами или с двумя
— 62 —

Мост цел.
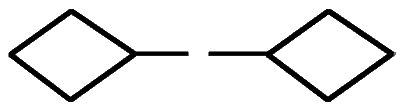
Мост разорван
нечетными (стр. 65)? Это особенная геометрия. Она называется геометрия положения или топология. Вот тебе, кстати, прекрасная фигурка. Попробуй нарисовать ее одним росчерком. Ее придумал когда-то геометр Листинг.
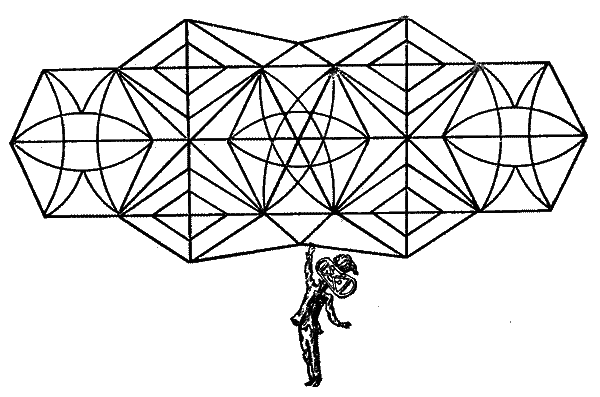
Фигура Листинга.
— Так, значит, — сказал Илюша, — на свете есть не одна геометрия? Не только та, которую мы учим в школе?
— Далеко не одна.
— А почему этот ваш командор еще и Кандидат Тупиковых Наук? Что это за науки?
— Ну, в лабиринте ты видел немало тупиков. Это они самые.
— А почему он Магистр Деревьев?
— Если из твоего первого чертежа с двумя ромбами я уберу мост, система путей потеряет связность, будет опять два отдельных ромба — и все. Линию, которая соединяет два узла, мы называем путем, а если путь имеет то свойство, что при удалении его система теряет связность и распадается, то мы такой путь и называем мостом. Может существовать система, состоящая только из тупиков и мостов.
Такая система называется деревом. В ней ни одного пути, который можно
— 63 —
было бы удалить без того, чтобы система не распалась. Ну, а теперь давай подумаем, нет ли чего-нибудь общего между двумя такими задачами: нарисовать уникурсальную фигуру одним росчерком и обойти лабиринт, у которого только один вход. Ты, я думаю, понимаешь, что любой лабиринт можно считать лабиринтом с одним входом, потому что всякий лабиринт мы всегда можем «обнести» еще одним «забором».

— Уж не знаю, — вымолвил не сразу Илюша. — Правда, быть может, если начертить план лабиринта не так, как мы его чертили до сих пор, а изображать линиями не стенки, а самые пути, как раз и получится такая фигура, которую нужно обойти или начертить…
— Постой, постой минуточку! — прервал Радикс его рассуждения. — А как ты полагаешь, нужно ли в таком случае вычерчивать точный план путей?
— Я должен быть точен в том смысле, чтобы на плане было то число перекрестков, какое есть на самом деле, и то же самое относительно путей между ними. А как именно я нарисую самые пути — это неважно, лишь бы не спутаться, куда какой из них ведет.
— Правильно, — резюмировал его собеседник. — Следовательно, вообще можно сказать, что ты интересуешься топологической схемой путей. Если ты представишь себе, что линии путей изображены нитками, которые связаны в узлах-перекрестках, то можешь как угодно деформировать, или видоизменять, «сетку путей» — топологическая схема останется не-
— 64 —
изменной. Ты только не должен рвать нитки, развязывать узлы или завязывать новые. Ну, а как же все-таки начертить такую фигуру?