Впрочем, обо всем этом ты узнаешь попозже[5]. Но это еще отнюдь не все… Самое главное в том, что попутно с этими решениями выяснено вполне и до конца, какие именно задачи можно решать с помощью циркуля и линейки, а какие нельзя, и почему нельзя. Вот в чем дело. А если ты уяснил, и почему какая-нибудь задача не имеет решения, то тогда ты можешь узнать, что именно тебе требуется для решения подобных задач.

— Извините… — произнес Илюша. — А с другими углами очень трудно?

— Не столь трудно, — отвечал с усмешкой Доктор Четных и Нечетных, — сколь замысловато…

— Когда готово, то нетрудно! — кротко заметила тетушка Розамунда, а язык ее, громко прищелкнув, вдруг нарисовал в воздухе чертеж. Все линии были голубоватые и очень приятно светились.

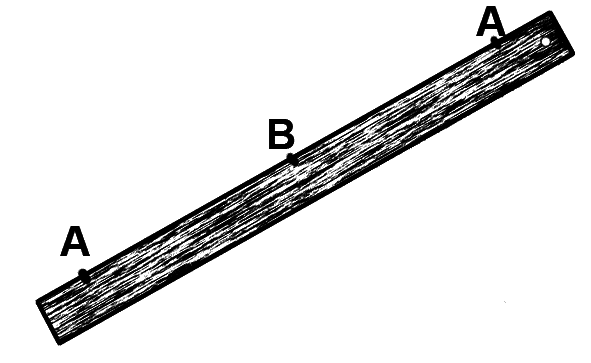
Линейка для невсиса с двумя отметками.

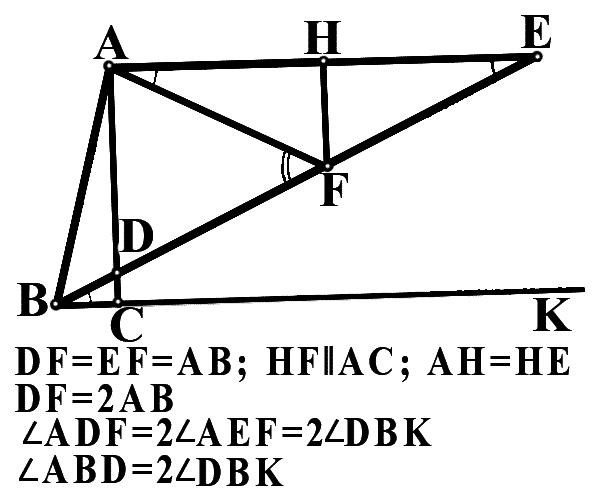
— Прелестный чертеж! — вежливо заметил доктор. — Ну-с, вот тебе угол ABC — 75°, а вот угол СВЕ — 25°. Но делается это не линейкой и циркулем, а линейкой, на которой есть две отметки — одна за другой, и каждая равна отрезку АВ. Этот способ в древности назывался способом невсиса. Через точку В надо провести прямую так, чтобы отрезок DE равнялся бы удвоенному отрезку АВ. При помощи вспомогательных прямых на чертеже нетрудно доказать, что угол AFD равен двум углам AEF…

— Как внешний угол по отношению к треугольнику AEF, — догадался Илюша.

— 49 —

— Точно… — протянула тетушка.

И у Илюши на душе стало на минутку полегче — он все-таки догадался. Ему хотелось еще кое о чем спросить, но доктор Уникурсальян не дал ему и рта раскрыть.

— Сделать можно, — возопил доктор, — а вот объяснить, почему надо делать так, а не иначе, то есть, почему этот способ в данном случае приводит к цели, — это потруднее!

— А когда-нибудь… — робко начал Илюша.

— Все должно двигаться в самом удивительном порядке, — заявила тетушка Розамунда, а ее неукротимый: язык принес откуда-то линейку с двумя отметками, приложил ее на чертеже к отрезку DE, и вышло точь-в-точь.

— Вот именно! — воскликнул доктор Четных и Нечетных — Это невсис Паппа Александрийца. Замысловато, а зато точь-в-точь! Терпи, мой любезнейший, сами греки тоже помучались как следует. А разобрать до конца не удалось. Только в шестнадцатом веке Франциск Виета разобрал[6]. Вот и смекай — нехитрая на вид задача, а в руки попросту не дается. — Вслед за этим доктор мрачно покосился на Илюшу и пробормотал угрожающе: — Внимание и молчание!..

— А ведь, пожалуй, теперь я начинаю соображать… — сказал Илюша.

— Прелестно! — отвечал командор. — Я вижу, что вы, любезнейший юноша, делаете некоторые успехи, как сказала одна заботливая мамаша, ухватив за ухо своего предприимчивого отпрыска в ту минуту, когда он забрался во вторую банку с вареньем.

— Только как это сделать? — со вздохом сказал Илюша. — То есть я не про варенье, а про невсис.

— Все в свое время, — отвечала Розамунда.

Она поглядела на Доктора Четных и Нечетных Узлов и сказала:

— Ну-с?

Доктор Узлов начал свою замечательную речь:

— Досточтимые и глубокоуважаемые друзья мои, слушательницы и слушатели! То, что я имею сказать вам в настоящей моей изумительной речи, так необыкновенно важно, так страшно серьезно, так дивно поучительно, что у меня, признаться, у самого заранее дух захватывает. И ты, о неопытный и желторотый юнец, неизвестно как затесавшийся в наш волшебный мир, повесь свои мохнатые уши на гвоздь внимания и восхищения…

Илюше очень хотелось обидеться, когда он услыхал про

— 50 —

чьи-то мохнатые уши, но он решил, что лучше уж притвориться, что не понимает, о ком тут идет речь.

— Понимаешь ли ты, достопочтенный слушатель, куда ты попал? Постигаешь ли ты, что великая наука наша — одна из древнейших наук мира; что именно на ней некогда человек чуть не впервые учился размышлять и доказывать; на ее примерах человек учил сам себя рассуждать, сам с собой обсуждал свои замыслы, сам научился поправлять их и в течение многих и многих столетий шел осторожнейшими шагами, дабы наконец овладеть тем, чем он сейчас владеет? Можешь ли ты вообразить себе, что много и много человеческих жизней трудолюбиво и самоотверженно положено на то, чтобы мир мог сделать хотя бы еще один шаг в науке? Сумеешь ли ты представить себе, что ты легко можешь услыхать здесь какое-нибудь занимательное слово, но для того, чтобы объяснить тебе, что обозначает это слово, нам всем придется положить немало труда? И поверь, что все мы готовы это для тебя сделать, но и ты должен стараться и относиться к каждому нашему слову так вдумчиво и так серьезно, как только позволяют тебе твои способности! Итак, начнем сначала! Я утверждаю, что путешествовать по нашим чудесным краям невозможно без неких мощных вспомогательных аппаратов. Вот первое, что должен я открыть вам, опираясь на всю силу моего прославленного красноречия, сиречь элоквенции. Что же это за аппараты и как ими пользоваться? Во времена великого Архимеда это были палочка и песок, а в наше время — это карандаш и бумага. Хотя, впрочем, никому не возбраняется, находясь на чистом воздухе, пользоваться для тех же целей палочкой и песочком. Кроме того, надо вооружиться самым прочным терпением: если ты чего-нибудь не понял, ты должен тотчас же возвратиться обратно и снова пуститься в путь в том же направлении. Имей в виду, что нет такого маршрута на свете, который не уступил бы твоему упорству. Все, что мы будем говорить и утверждать, должно быть полно совершенно определенного смысла, и все это должно быть выражено в сжатой, ясной, совершенно недвусмысленной и легко запоминающейся форме. Как это делается, понять очень легко: подражайте мне, и всё! Однако я вынужден идти еще далее. Дело в том, что я требую, и ты требуешь, и мы требуем, и все, кто может нас услыхать, требуют, чтобы все вводимые нами новые наименования, способы выражения и обозначения были исчерпывающим образом объяснены, то есть определены. Всякое заключение наше или вывод, то есть равенство, неравенство, какая-нибудь формула, а также всякое словесное или иное (а стало быть, бессловесное!) утверждение, с полной необходимостью должны вытекать из того, что было принято нами

— 51 —

ранее в качестве условия или было ранее доказано, то есть из наших предпосылок.

Клянусь вам, что это самый непреложный закон в нашем хитроумном мире, где все подчинено Дедукции, что обозначает, как вам, быть может, известно, «вывод», или «заключение». Надо всегда подумывать и о том, есть ли на что сослаться, если ко мне начнут придираться по этому самому поводу самые хитрые, самые сварливые, самые несговорчивые придиры на всем белом свете?.. Когда ученым приходится удостовериться, что некоторая задача совершенно не разрешима известными им способами, то нередко это ведет к глубоким переменам в самой науке. Кажется, чего уж проще — вычислить диагональ квадрата со стороной, равной единице?

Извлек из двойки квадратный корень — и готово! Но когда в древности ученые греки впервые убедились в том, что в точности они это вычисление проделать не могут, то целая система математических воззрений была ниспровергнута! Наш волшебный мир, видишь ли, это очень серьезный волшебный мир: прошу не забывать!

Тут Магистр Деревьев надменно обвел сверкающим взором своих притихших слушателей и продолжал с новой силой:

— Помните: следует знать и нельзя ни в коем случае забывать о том, что-то, что необходимо, не всегда достаточно, а что достаточно, не всегда необходимо. А потом не забывайте о том, чтобы весь ход ваших рассуждений определялся четко поставленным вопросом, чтобы вы не упускали на каждом шагу поставленную вами цель. С другой стороны, смотрите, не внесли ли вы в суждения ваши чего-либо лишнего, что не было предусмотрено теми условиями или ограничениями, которые вы имели в виду. Помните: раз вам даны для задачи некоторые условия, то все они до одного должны быть использованы в решении так или иначе, а если какое-нибудь условие окажется лишним, то и это должно быть установлено с полной убедительностью, о чем мы еще потолкуем с вами в Схолии Седьмой. При этом надо знать, что это правило касается не только тех случаев, когда речь идет об обычном, или «положительном», решении задачи, которое в то же время должно являться общим решением для многих задач, подобных данной. Оно касается также и тех, нередко гораздо более трудных случаев, когда мы собираемся установить, что у нас нет возможности найти в данной области искомое или выполнить заданное предписанным способом, как заметил один прилежный юноша, подавая своему преподавателю на контрольной работе чистый лист бумаги…