При обсуждении задачи об интерференции говорилось, что если попытаться обнаружить, находится ли фотон в состоянии T1, поместив детектор в первое плечо интерферометра, то состояние суперпозиции, необходимое для интерференции, будет разрушено. Состояние суперпозиции T превратится либо в T1, либо в T2. Поскольку состояние T является суперпозицией в равных пропорциях T1 и T2, в половине измерений результатом будет обнаружение системы в состоянии T1, а в другой половине — T2. В каждом конкретном измерении невозможно заранее узнать, какой будет получен результат. Большое число измерений покажет, что суперпозиция имеет пропорцию 50:50, поскольку в половине случаев фотон обнаружится в первом плече прибора (состояние T1), а в половине случаев — во втором плече (состояние T2).
Суперпозиция собственных значений импульса, показанная на рис. 6.5, состоит из огромного (бесконечного) числа состояний, лежащих в диапазоне импульсов, характеризуемом шириной распределения ∆p. Таким образом, существует широкий диапазон значений импульса, которые могут быть получены в любом отдельном измерении. Если выполнить единичное измерение, будет получено одно из множества этих значений.
Допустим, мы выполнили измерение и обнаружили, что импульс немного больше p0. Обозначим его p1, поскольку это наше первое измерение. В процессе выполнения измерения мы произвели возмущение системы, которым нельзя пренебречь. Она перешла из состояния суперпозиции в состояние с единственным собственным значением импульса p1. Таким образом, для выполнения ещё одного измерения понадобится начать всё сначала и подготовить частицу (систему) тем же способом, которым она была подготовлена изначально, чтобы получить такое же распределение импульсов.
Теперь выполняем второе измерение. На этот раз мы получаем значение, которое несколько меньше p0. Обозначим его p2. Вновь подготовим систему и выполним ещё одно измерение. Назовём результат p3. Каждый раз, выполняя измерения одинаково подготовленных систем, мы будем получать разные конкретные значения импульса. Заранее неизвестно, какое получится значение. Если выполнить очень много измерений, можно построить график вероятности получения различных значений p. Такой график даст распределение, подобное тому, что представлено на рис. 6.5. Невозможно предсказать, какое значение будет получено в отдельном измерении. Однако кое-что нам всё же известно. Весьма маловероятно, что будет получено значение p, которое намного больше или намного меньше p0, поскольку распределение имеет очень малую амплитуду на краях диапазона. Скорее всего, измеренное значение p будет находиться вблизи p0, потому что именно в этой части распределения велика амплитуда.
Импульс частицы в состоянии суперпозиции определён не вполне чётко
Частица, находящаяся в суперпозиции собственных состояний импульса, вроде представленной на рис. 6.5, не имеет чётко определённого значения импульса. Нельзя предсказать, какое его значение будет получено в одном конкретном измерении. Можно утверждать, что, скорее всего, будет получено значение, близкое к p0. Выполнив много измерений, можно найти распределение вероятности.
Классическая частица, подобная той, что показана на рис. 2.5, имеет чётко определённое значение импульса. Измерить это значение можно, не изменяя его. Если частица свободна, можно выполнять новые измерения импульса в разные моменты времени, и всегда будет получено одно и то же значение p. Однако это совсем не так в случае абсолютно малых квантовых частиц, находящихся в состоянии суперпозиции по импульсу. В единичном измерении мы получим одно конкретное значение p, но сам акт измерения фундаментальным образом меняет природу частицы. Частица переходит из состояния суперпозиции в одно из собственных состояний (одиночная волна с единственным значением импульса). Из состояния, в котором существует распределение вероятности по импульсам, частица переходит в состояние с единственным значением импульса — тем, которое наблюдалось. Чтобы восстановить распределение, частицу необходимо подготовить заново.
Где находится частица, когда она пребывает в состоянии суперпозиции по импульсу?
При обсуждении рис. 6.1 говорилось, что частица, находящаяся в отдельном собственном состоянии импульса, делокализована по всему пространству. Это совсем не согласуется с описанием фотоэлектрического эффекта, поэтому теперь возникает вопрос: где находится частица, которая пребывает в состоянии суперпозиции? Определённый намёк на ответ мы уже получили, обсуждая рис. 6.2–6.4. Из рис. 6.3 и 6.4 видно, что суперпозиция волн разной длины порождает распределение, которое концентрируется в некоторой области пространства. На рис. 6.3 длина волны изменяется от 0,8 до 1,2 и распределение выглядит не столь сильно сконцентрированным в одной области, как на рис. 6.4, где длина волны изменяется от 0 до 4. На рис. 6.6 показано пространственное распределение, соответствующее распределению волн (импульсных собственных состояний), изображённому на рис. 6.5. Есть положение, где пространственное распределение достигает максимума, и это положение также является средним. Для значений x, больших и меньших, чем x0, амплитуды (вероятности) становятся меньше.
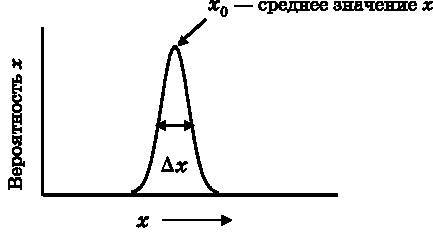
Рис. 6.6. График вероятности обнаружения частицы в точке x, когда она находится в суперпозиции собственных состояний по импульсу, показанной на рис. 6.5. Точка x0 соответствует среднему положению с наибольшей вероятностью. Величина ∆x служит мерой ширины пространственного распределения
Что означает распределение вероятности положений (значений x)? Частица с распределением вероятности по импульсам, изображённым на рис. 6.5, даёт пространственное распределение вероятности, представленное на рис. 6.6. Одиночное измерение положения даёт конкретное значение координаты. Обозначим его x1. Выполнение измерения абсолютно малой квантовой частицы вызывает возмущение, которым нельзя пренебречь, что приводит к коллапсу пространственного распределения вероятности до собственного значения с чётко определённой координатой. Чтобы выполнить другое измерение, систему (частицу) надо подготовить заново прежним способом, тогда она будет иметь такое же распределение вероятности по импульсу и, следовательно, такое же пространственное распределение вероятностей. Второе измерение положения частицы даст значение x2, которое в общем случае не будет совпадать с x1. Если, подготавливая систему вновь и вновь, выполнить много измерений положения, обнаружится распределение вероятности по координате, изображённое на рис. 6.6. Величина ∆x служит мерой ширины пространственного распределения. Пространственное распределение, изображённое на рис. 6.6, определённое по множеству измерений идентично подготовленных систем, говорит о вероятности получить при измерении любое конкретное значение положения. С наибольшей вероятностью измерение обнаружит частицу где-то вблизи точки x0, но для любого отдельного измерения невозможно сказать, где будет найдена частица. В то же время мала вероятность получить при измерении положения значение, далёкое от x0.