И боюсь, никто уже не скажет это. Потому что все богатство архивных материалов ничего не добавит нам о той второй и главной его жизни, что начиналась за дверями его кабинета, когда он оставался наедине со своими выкладками. Лишь одно, быть может, чуть открывает нам его.

В 1853 году умер его любимец Алексей. И за несколько месяцев Николай Иванович Лобачевский превратился в дряблого, больного старика. Он начал слепнуть, и болезнь прогрессировала быстро и неуклонно.

Ему осталось жизни три года; по заведенному порядку он еще пытался сохранить привычный уклад, пытался еще что-то делать по службе, но жизнь уже ушла.

И, вспоминая, как заставлял он сына штудировать математику, как, обычно сдержанный и спокойный, криком и простыми словами поносил его, когда тот бездельничал; как величаво радостно появлялся на мгновение в дверях его комнаты, где сын праздновал с друзьями удачный экзамен: «Продолжайте, господа, не буду вам мешать», — вспоминая все, я думаю, этого замкнутого, сурового человека поддерживала одна лишь романтическая мечта: сын продолжит его Геометрию.

И смерть сына означала и его собственную смерть. А беда никогда не приходит одна. И эти последние три года одна за другой приходят беды к Лобачевскому.

Но, вероятно, он уж не слишком видит их. Все уже кончено. И единственное, что еще осталось, — его Геометрия.

Слепой, он закончил диктовать последний свой труд, когда почти уже не оставалось дней его.

Глава 9

Неевклидова геометрия. Иллюстрации

Сейчас мы чуть-чуть заглянем в некий музей «курьезов». Курьезов лишь потому, что наша интуиция, воспитанная на евклидовой геометрии, все время противится восприятию геометрии Лобачевского.

Для того чтобы наши чувства высказались за полное теоретическое равноправие обеих геометрий, необходимо очень основательно и долго изучать геометрию Лобачевского.

И тогда то, что на первый поверхностный взгляд представлялось нелепым и парадоксальным, начинает светиться спокойной, холодной красотой логики и истины.

Между прочим, коль скоро все время говорится о красоте, можно заметить, что полностью аналогичные вещи часто бывают и в искусстве.

Те самые картины импрессионистов, которые сейчас, видимо, восхищают подавляющее большинство зрителей, у посетителей художественных салонов конца прошлого столетия вызывали насмешливый хохот. Реакция той же природы, что отношение современников к работам Лобачевского. Вообще надо заметить, что, к великому сожалению, не слишком сложная мысль «прежде чем судить, постарайся понять» — еще до сих пор откровение для многих.

Клочки искаженной, исковерканной информации, случайно залетевшие в сознание, слишком часто принимаются за достаточное основание для авторитетных суждений. Неважно — благожелательных или уничтожающих. Кстати, геометрии Лобачевского в этом смысле забавным образом не повезло еще один раз.

Еще много лет назад в статьях некоего весьма уважаемого писателя мне встретилась фраза: «Лобачевский доказал, что линии, параллельные у Евклида, пересекаются в бесконечности». Затем в связи с этим шли какие-то вполне умные, широкие и обобщающие рассуждения. Не помню уже о чем. Чуть ли не о том же, о чем пишу сейчас я.

По только что отмеченной склонности к поверхностным суждениям я решил, что этот автор вообще ничего не слышал о геометрии Лобачевского. Но эта же самая фраза столь настойчиво повторялась в статьях и книгах других литераторов, что в один прекрасный день меня озарило. Речь идет о параллельных в смысле Лобачевского… «А то, что эти линии совсем не «евклидовы параллельные», мы увидим полстраницей позже. Между ними такое же примерно соотношение, как между пилотом в средневековье (штурман корабля) и пилотом в современном понимании. Единый термин, используемый для обозначения разных понятий, породил эту чехарду в представлениях далеких от математики людей. Быть может, очень строгого суда они и не заслуживают, но уж и поощрения, бесспорно, тоже.

Чтобы закончить притчу, я могу сообщить, что потом отыскался и видимый первоисточник «литературного варианта геометрии Лобачевского».

Оказывается, грешен сам Федор Михайлович Достоевский. А писал он вещи весьма примечательные. В «Братьях Карамазовых» Иван Федорович, объясняя Алеше свое морально-философское кредо, в частности, говорит:

«Но вот что, однако, надо отметить: если бог действительно есть и если он действительно создал землю, то, как нам совершенно известно, создал он ее по евклидовой геометрии, а ум человеческий с понятием лишь о трех измерениях пространства. Между тем находились и находятся даже и теперь геометры и философы, и даже из замечательнейших, которые сомневаются, чтобы вся вселенная или, еще обширнее — все бытие было создано лишь по евклидовой геометрии, осмеливаются даже мечтать, что две параллельные линии, которые по Евклиду ни за что не могут сойтись на земле, может быть, и сошлись бы где-нибудь в бесконечности. Я, голубчик, решил так, что если я даже этого не могу понять, то где же про бога понять. Я смиренно сознаюсь, что у меня нет никаких способностей разрешать подобные вопросы, у меня ум евклидовский, земной, а потому где нам решать, что не от мира сего».

Я не думаю отождествлять здесь самого Достоевского и Ивана Карамазова, и сейчас можно вообще отбросить обсуждение проблемы бытия божия. Но о геометрии-то пишет сам Достоевский. Это его представления. И то, что написано великолепно, показывает, как неглубокая, поверхностная интуиция поверхностного дилетанта невольно возводится в абсолют. Во всей фразе, если разбирать строго, нет буквально ни одной верной мысли. Это тем интереснее, что великолепный, чисто аналитический ум автора тоже чувствуется в каждом слове.

Далее Иван Федорович доводит свое интеллектуальное чудачество по поводу геометрии до логического предела, распространяя его даже на физику:

«Пусть даже параллельные линии сойдутся, и я сам это увижу; увижу и скажу, что сошлись, а все-таки не приму».

Надеюсь, понятно, что по этому отрывку я не собираюсь делать какие-либо малейшие выводы о творчестве Достоевского вообще. И надо иметь в виду, что геометрия Ивана Карамазова совсем не интересует. Для него это лишь случайный пример — иллюстрация его идей.

Но для нас это иллюстрация и искаженного представления о науке, и легкомысленных рассуждений о непонятных вещах, и довольно-таки явного обскурантизма Ивана Карамазова.

Впрочем, можно оправдать самого Достоевского по крайней мере в том смысле, что фактической ошибки он-то, быть может, и не допускал.

Имена геометров не названы, и потому можно надеяться, что Иван пересказывал представления римановой либо проективной геометрии.

Но поскольку, с одной стороны, слова «неевклидова геометрия» ассоциируются с именем Лобачевского, а с другой — все культурные литераторы, безусловно, внимательно читали Достоевского, то слова Ивана в дальнейшем неизменно экстраполировались к Лобачевскому.

Все эти литературно-психологические изыскания, помимо общих идей дидактически-назидательного характера, возможно, полезны тем, что на таких примерах становится понятней интеллектуальная смелость Бояи и Лобачевского.

А теперь, успокоив душу, вернемся в наш музей.

Естественно, мы ограничимся лишь несколькими теоремами и совсем не будем говорить о стереометрии. Поэтому дальше нигде не будем оговариваться, что все это происходит в одной плоскости.

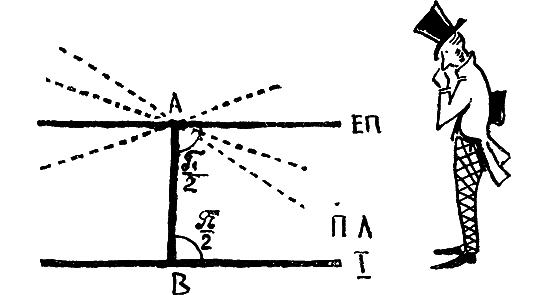
Сначала, конечно, постулат Бояи — Лобачевского — антагонист «евклидова пятого».

«Через данную точку к данной прямой, кроме «евклидовой параллельной», можно провести по крайней мере еще одну прямую, не встречающую данную».

Отсюда немедленно следует, что можно провести и бесконечное число таких прямых.