5. (α & (β V γ)) = ((α & β) V (α & γ)) (закон дистрибутивности, или распределительности, конъюнкции относительно дизъюнкции).
6. (α V (β & γ)) = ((α V β) & (α V γ)) (закон дистрибутивности дизъюнкции относительно конъюнкции).
7. (α & (α V β)) = α (первый закон поглощения).
8. (α V (α & β)) = α (второй закон поглощения).
9. ~(α & β) = (~α V ~β) (первый закон Де Моргана).
10. ~(α V β) = (~α & ~β) (второй закон Де Моргана).
11. (α & α) = α (закон идемпотентности для конъюнкции).
12. (α V α) = α (закон идемпотентности для дизъюнкции).
13. ~~α = α (закон снятия двойного отрицания).
14. (α & 1) = α (закон отбрасывания единицы).
15. (α V 0) = α (закон отбрасывания нуля).
16. (α & ~α) = 0 (закон противоречия, выраженный в форме приравнивания противоречия нулю).
17. (α & ~α)=1 (закон исключенного третьего, выражений в форме равенства).
Перечисленные постулаты[6] являются не аксиомами, а схемами аксиом. Это значит, что, каждый постулат задает бесконечное множество аксиом определенной структуры. Так, схема аксиом 1 задает аксиомы: (А1 & А2) = (A2 & A1), ((А1 V ~A2) & ~A1) = (~A1 & (A1 V ~A2)) и т.д.; аксиомы — это равенства, принимаемые в качестве исходных.
Схемы аксиом 1 и 2 задают свойство перестановочности членов в конъюнктивных и дизъюнктивных формулах. Схемы аксиом 3 и 4 выражают ассоциативные законы, подобные ассоциативным законам школьной алгебры, где, как известно, (а • b) • с = а - (b • с) и (а + b) + с = a + (b + с). В школьной алгебре имеется только один дистрибутивный закон — закон дистрибутивности умножения относительно сложения: A • (b + с) = a • b + A • с, так как обычное сложение чисел не дистрибутивно относительно обычного умножения (то есть неверно, что для любых чисел а, b и с
а + (b • с) = (а + b) • (а + с)).
В данной же системе обе операции, конъюнкция и дизъюнкция, дистрибутивны одна относительно другой (схемы аксиом 5 и 6). Смысл законов Де Моргана[7] (схемы аксиом 9 и 10) можно передать фразами: «Отрицание конъюнктивной формулы означает дизъюнкцию отрицаний ее членов»; «Отрицание дизъюнктивной формулы означает конъюнкцию отрицаний ее членов». Смысл схем аксиом, выражающих остальные законы, непосредственно ясен. Заметим лишь, что они служат эффективным средством упрощения формул рассматриваемой формальной системы, то есть построения по данной формуле таких равных ей формул, которые проще, чем исходная (в том смысле, что содержат меньшее число вхождений логических связок); ср. ниже, с. 75—76.
[b]. Правила вывода.
Если верно равенство α = β, то верно и равенство Ф[α] = Ф[β]. Здесь Ф[α] есть произвольная формула, содержащая в качестве своей части, формулу α (аналогично понимается и Ф[β]). Это — правило замены равным (ср. выше с. 42), но «приуроченное» специально к нашему формальному аппарату. Смысл правила состоит в том, что в произвольной формуле Ф[α], в которую входит α, можно α в любом ее вхождении заменить на какую угодно равную ей формулу β и в результате получится формула Ф[β], равная формуле Ф[α][8].
В дополнение к этому правилу мы будем в процессе переработки равенств пользоваться известными свойствами отношения равенства — рефлексивностью (для любой формулы α справедливо α = α), симметричностью (для любых α и β из α = β следует β = α) и транзитивностью (если α = β и β = γ, то α = γ)[9]. Таким образом, процедуры вывода в данном исчислении представляют собой обычные тождественные преобразования.
V. Определения.
Записи вида (α ≡ β) и (α → β) суть сокращения для формул вида (~α V β)[10] и ((~α V β) & (α V ~β)).
Приведенное исчисление представляет собой исчисление равенств формул определенного вида — исчисление, которое в алгебраических терминах носит название исчисления равенств булевых выражений[11]. Оно сформулировано нами как неинтерпретированное исчисление, поскольку при его развертывании не было указано, из какой же области следует брать значения пропозициональных переменных, как следует понимать логические связки и константы 0 и 1, какой смысл имеют формулы и как нужно понимать содержание термина «верная формула».
Дадим теперь первую интерпретацию этого исчисления — функциональную.
Функциональная интерпретация
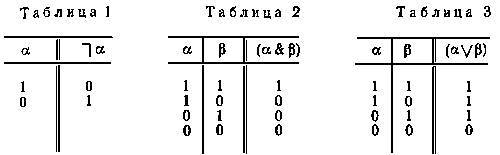
Пропозициональные переменные истолковываются как переменные для чисел 0 и 1 (то есть каждая из переменных может принимать только эти два значения). Сложные формулы (формулы, отличные от пропозициональных переменных) интерпретируются следующим образом. Каждая связка понимается как функция, которая значениям аргументов (аргумента) — нулю или единице — ставит в соответствие значение функции (которое тоже может быть только либо нулем, либо единицей). Значения связок строятся на основе табличных определений (табл. 1, 2, 3)[12].
Значения знаков → и ≡ вытекают из этих таблиц. В силу того, что (α → β) есть сокращение для (~α V β), (α ≡ β)—сокращение для ((~α V β) & (α V ~β)); можно считать, что знаки → и ≡ задаются таблицами 4 и 5 соответственно.
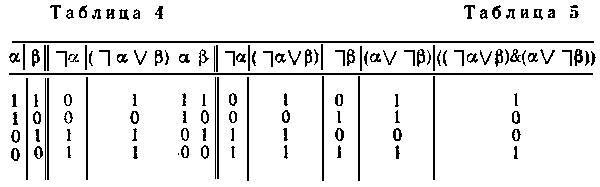
Поясним, как строится, например, табл. 5. Мы начинаем с того, что строим колонку для формулы ~а, пользуясь табл. 1, задающей операцию (функцию) отрицания; затем, пользуясь табл. 3, определяющей функцию, называемую дизъюнкцией, строим колонку для формулы (~α V β) аналогичным образом строится колонка для формулы (α V ~β) наконец, опираясь на табл. 2, задающую функцию, называемую конъюнкцией, мы строим колонку для конъюнкции ((~α V β) & (α V ~β)) Задание функции ≡ получено: его дают две первые левые (аргументные) колонки табл. 5 и ее крайняя правая колонка.
Задав описанным способом интерпретацию пропозициональных переменных и связок, мы тем самым получаем интерпертацию и для любой формулы[13]: каждая формула осмысливается как функция (таблица), которая может быть построена по данной формуле.
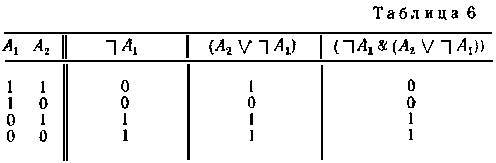
Возьмем, например, формулу (A1 & (A2 V ~A1)) и определим, какую функцию она задает, построив соответствующую таблицу (табл. 6).
Построим таблицу для формулы (А1& ~(А2 V A1))» проверку правильности которой мы выше предоставили читателю. Мы получим табл. 7.

Из нее видно, что эта формула принимает значение 0 при любых значениях своих аргументов. Она называется поэтому тождественно равной нулю. Если мы возьмем отрицание только что рассмотренной формулы, то есть формулу ~(А1 & ~(А2 V A1)), то очевидно, что она задает функцию, которая принимает значение 1 при любых значениях своих аргументов, то есть функцию, тождественно равную единице.
Функции, тождественно равные нулю, неотличимы друг от друга: ведь какие бы значения ни принимали аргументы (и сколько бы их ни было), функции эти все равно принимают одно и то же значение, то есть ведут себя как константы—постоянные. То же самое можно сказать и о функциях, тождественно равных единице. Учитывая это, функции, тождественно равные нулю, мы отождествим с константой 0, а функции, тождественно равные единице, с константой 1 (и, следовательно, будем считать, что значением первой константы является число 0, а второй — число 1).
Для завершения интерпретации нам осталось только установить, при каких условиях равенство α = β следует признать верным (истинным). Будем считать, что α = β есть верное равенство, если α и β задают одну и ту же функцию, то есть, что если построить таблицы, соответствующие формулам α и β, таблицы эти полностью совпадут[14].