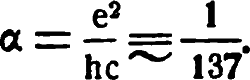
Эта чрезвычайно важная физическая величина часто называется константой связи электромагнитных взаимодействий.

Тот факт, что она мала по сравнению с единицей, значительно облегчает все расчеты в квантовой электродинамике и упрощает конкретные модели тех или иных процессов. Благодаря малости константы связи теоретикам удалось построить хорошие методы расчета различных наблюдаемых характеристик электромагнитных взаимодействий, и их результаты на сегодняшний день превосходно согласуются с экспериментальными данными.

Казалось бы, если есть такое согласование, то все хорошо. Но теоретики на этом не остановились — они решили проверить, сохранится ли столь приятная картина и в дальнейшем, то есть при переходе к сколь угодно малым расстояниям, на которых происходит взаимодействие. Исследуя эту проблему, советские физики Л. Ландау, И. Померанчук и другие пришли к неутешительному выводу, что квантовая электродинамика в ее современной форме вообще неприменима к описанию процессов, происходящих с участием бесструктурных точечных электронов на очень малых расстояниях. Конкретно их результаты сводились к весьма парадоксальному положению: при попытке описать поведение зарядов и квантов электромагнитного поля в очень малых областях пространства оказывалось, что взаимодействие на больших расстояниях… исчезает!

Конечно же, этот факт противоречит известным результатам наблюдений и должен рассматриваться как своеобразный способ доказательства «от противного», доказательства того, что электродинамика не является полностью удовлетворительной теорией и должна быть существенно изменена для описания процессов при очень высоких энергиях и на очень малых расстояниях. В чем же суть полученных противоречий?

А в том, что представления электродинамики требуют рассмотрения особого типа объектов — виртуальных частиц.

Виртуальные частицы обычно имеют те же названия, что и реальные, скажем, фотоны или электроны, но обладают одним важным свойством, отличающим их от реальных частиц, — они испускаются и поглощаются непосредственно в микроскопически малой области взаимодействия и никогда не вылетают наружу и не регистрируются макроскопическими приборами. Скажем, электрон в процессе движения может как бы взаимодействовать сам с собой, испуская и тут же поглощая фотоны. В свою очередь, фотон может превратиться в пару, состоящую из электрона и позитрона, которые сразу же, вслед за образованием, снова аннигилируют, превращаясь в фотон.

Благодаря этим процессам реальный электрон должен непрерывно излучать и поглощать фотоны: он словно одевается в своеобразную «шубу» из виртуальных фотонов и электрон-позитронных пар. Чем глубже мы пытаемся проникнуть к центру электрона, тем более плотной становится его «шуба». На достаточно больших расстояниях электрон выглядит как точечный объект, несущий определенный электрический заряд. Но когда мы попытаемся узнать заряд «голого» электрона, без всякой «шубы» из виртуальных частиц, то есть настоящего точечного электрона, то окажется, что этот заряд бесконечно большой.

Такое положение крайне неудовлетворительно. Ведь физика всегда имела дело с зарядами, обладающими конечными — пусть очень большими, но конечными! — значениями. А тут получается совершенно неприемлемое бесконечное значение. Можно ли избежать этой неприятности?

Оказывается, можно, но весьма дорогой ценой. Можно просто считать, что электрический заряд «голого» электрона, для которого как бы не существует взаимодействия с фотонами, имеет конечное значение. Но тогда неизбежно получается, что заряд реального электрона вообще должен быть равен нулю и тогда он не сумеет взаимодействовать с фотонами и другими зарядами. Такая картина формально допустима, но она противоречит известному факту — реальные электроны все-таки имеют заряды.

Итак, в любом случае — конечен заряд «голого» точечного электрона или бесконечен — мы приходим к неприемлемой картине.

Несмотря на довольно сложный характер теории, причина всех трудностей довольно проста и наглядна.

Обсудим следующий пример. Пусть в вещество, где существует равное количество положительных и отрицательных зарядов, вводится новый, скажем для определенности, отрицательный заряд. При этом равновесие между различными зарядами вещества, конечно, нарушится. Новый заряд начнет притягивать к себе заряды противоположного знака, то есть положительные. Постепенно вблизи него будут накапливаться положительные заряды, в конце концов он окажется как бы заэкранированным и его действие на остальные заряды вещества практически прекратится.

Нечто подобное происходит и с «голым» электроном. Веществом, которое его экранирует, являются как раз виртуальные частицы, которые неизбежно появляются при учете взаимодействия. Квантовая электродинамика позволяет оценить эффективность этой экранировки, и оказывается, что заряд экранируется бесконечно сильно! Поэтому неудивительно, что, приписав «голому» электрону конечный электрический заряд, мы приходим к выводу, что этот заряд полностью экранируется «шубой» реального электрона, который и должен наблюдаться на опыте. И получается неприятный результат — этот реальный электрон должен выглядеть как частица с нулевым электрическим зарядом!

Чтобы прорвать бесконечно сильную экранировку, разумеется, необходимо приписывать «голому» электрону бесконечно большой заряд, что, как мы уже видели, тоже неудовлетворительно.

Вот с такими трудностями пришлось столкнуться теоретикам при попытке проверить применимость квантовой электродинамики к описанию процессов в сколь угодно малых областях пространства. Эти трудности и заставили их искать новый подход к описанию взаимодействий на малых расстояниях.

Но, прежде чем было достигнуто такое понимание проблемы, теоретики успели проделать довольно большую работу по построению моделей слабых и сильных взаимодействий по образцу квантовой электродинамики.

Как вы помните, первой моделью слабых взаимодействий оказалась теория бета-распада, предложенная Э. Ферми. Согласно этой теории нейтрон трансформировался в протон, излучая пару: электрон и антинейтрино. Э. Ферми в значительной степени исходил из аналогии с квантовой электродинамикой, но в его теории место фотона как бы занимала пара, состоящая из лептона и антилептона. Впоследствии его идея была расширена и позволила описать все распады сравнительно долгоживущих частиц как проявление некоторого универсального слабого взаимодействия.

Характерной особенностью этой теории является следующее представление: четыре частицы — барионы или лептоны — непременно взаимодействуют в одной точке, то есть в непосредственном контакте друг с другом. С помощью такого представления можно описать и распады частиц, и их рассеяние. Скажем, отрицательно заряженный мюон способен распадаться на электрон и пару, состоящую из электронного антинейтрино и мюонного нейтрино. В данном случае взаимодействие выглядит как контакт четырех лептонов. Это же представление позволяет описать и другой процесс, например, столкновение мюона с электронным нейтрино. В результате этого столкновения должны образоваться электрон и мюонное нейтрино.

В случае бета-распада взаимодействие выглядит как контакт двух барионов и двух лептонов. И опять на основе этого же представления можно было описать другие типы процессов, например, рассеяние электронного нейтрино на нейтроне, в результате которого возникал протон и электрон.

Обратите внимание на то, что в обоих случаях описания рассеяния возникает четкая закономерность превращения заряженных частиц в незаряженные и наоборот. Заряженный мюон трансформируется в мюонное нейтрино, а электронное нейтрино — в электрон. Или: нейтрон трансформируется в протон, а электронное нейтрино — опять-таки в электрон.