В частном виде, при экспериментировании с монохордом можно было получить такое выражение: 12/9 = 8/6. При этом 9 — среднее арифметическое 12 и 6, а 8 — среднее гармоническое. Дальше, скорее всего, были обнаружены и такие равенства: 2/1 = 3/2:3/4. Численно был выражен целый тон, как разница между квинтой и квартой: 3/2:4/3 = 9/8. Естественно, что еще Пифагор и его ученики придали обнаруженным закономерностям, кроме научного, и мистический смысл. Числа, с помощью которых можно было выразить музыкальные интервалы, составили тетрактиду. Вот пример того, как вместе с математической теорией музыки могла развиваться и теория пропорций.
Теперь подробнее рассмотрим теорему, названную в честь нашего героя. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов двух катетов. И вавилоняне, и египтяне были знакомы с этим утверждением задолго до Пифагора и использовали его знание в практических целях. Конечно же, задаваясь вопросом о том, кто открыл теорему Пифагора, мы, прежде всего, интересуемся тем, кто ее доказал. Споры об этом не прекращаются до сих пор, и вряд ли исследователи когда-нибудь придут к единому мнению по данному вопросу. Сложность решения этой проблемы связана не только с якобы бытовавшей среди пифагорейцев традицией приписывать свои открытия Пифагору. В свидетельствах биографов встречаются противоречия, которые ставят под сомнение авторство Пифагора. Так, Диоген Лаэртий пишет:
В день, когда Пифагор открыл свой чертеж знаменитый,
Славную он за него жертву быками воздвиг.
Долгое время эта цитата считалась серьезным косвенным доказательством того, что на самом деле не Пифагор доказал теорему, названную его именем. Ведь такое свидетельство противоречит представлению о Пифагоре как о вегетарианце и факту, что он учил не приносить в жертву животных. Но, как мы уже писали выше, современные исследователи считают, что запрет на принесение в жертву животных, на самом деле, был приписан ученому позже. Поэтому в качестве серьезного возражения против авторства Пифагора такой довод рассматриваться не может. С другой стороны, есть косвенное подтверждение того, что именно Пифагор первым доказал знаменитую теорему. Дело в том, что ее первое доказательство вполне могло вытекать из той же самой теории пропорций. Предположительно оно могло выглядеть следующим образом.
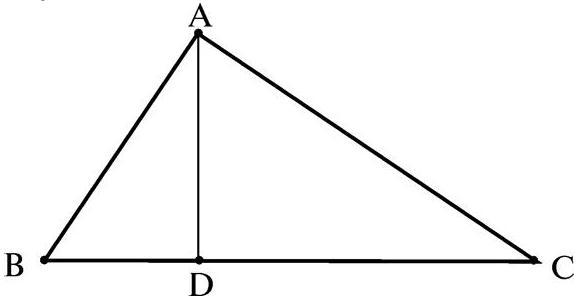
Треугольники ABC, ABD и ACD подобны. Следовательно их стороны пропорциональны:
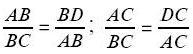
Следовательно:
АВ 2 = BC*BD и АС 2 = BC*DC
Сложив эти уравнения, получаем:
АВ 2 + АС 2 = BC(BD + DC); АВ 2 + АС 2 = ВС 2
Пифагор создал учение о четных и нечетных числах. Он дал определения этим видам чисел и исследовал их свойства. Историки математики считают, что приведенные ниже утверждения из 9-й книги «Начал» Евклида восходят к Пифагору и переданы практически в неизмененном виде.
21. Если складывается сколько угодно четных чисел, то целое будет четным.
22. Если складывается сколько угодно нечетных чисел, количество же их будет четным, то целое будет четным.
23. Если складывается сколько угодно нечетных чисел, количество же их будет нечетным, то и целое будет нечетным.
24. Если от четного числа отнимается четное, то остаток будет четным.
25. Если от четного числа отнимается нечетное, то остаток будет нечетным.
26. Если от нечетного числа отнимается нечетное, то остаток будет четным.
27. Если от нечетного числа отнимается четное, то остаток будет нечетным.
28. Если нечетное число, умножая четное, производит что-то, то возникающее будет четным.
29. Если нечетное число, умножая нечетное число, производит что-то, то возникающее будет нечетным.
30. Если нечетное число измеряет (является делителем) четное число, то оно будет измерять и его половину.
31. Если нечетное число по отношению к некоторому числу будет первым, то оно будет первым и по отношению к его удвоенному.
32. Из чисел, получаемых удвоением от двойки, каждое будет только четно-четным (см. ниже).
33. Если число имеет нечетную половину, то оно будет только четно-нечетным.
34. Если число не будет из получаемых удвоением от двойки и не имеет нечетную половину, то оно будет и четно-четным и четно-нечетным.
Терминология, используемая Евклидом, изложена в начале 7-й книги. Часть из используемых определений, по всей видимости, тоже восходит к Пифагору.
6. Четное число есть делящееся пополам.
7. Нечетное же — не делящееся пополам или отличающееся на единицу от четного числа.
8. Четно-четное число — есть четным числом, измеряемое четным числом (раз).
9. Четно же нечетное есть четным числом, измеряемое нечетное число (раз).
10. Нечетно-четное число есть нечетным числом, измеряемое четное число (раз).
11. Нечетно-нечетное число есть нечетным числом, измеряемое нечетное число (раз).
О том, что именно Пифагор занимался изучением свойств четных и нечетных чисел, свидетельствуют Аристотель и Аристоксен. Едва ли можно предположить, что эти ученые приписывали Пифагору «честь» открытия вполне очевидных истин. Здесь, как и в случае с теоремой Пифагора, заслугой, безусловно, является доказательства приведенных утверждений. Следовательно, ученый впервые применил дедуктивный подход к арифметике.
Единственное незначительное отличие, содержащееся в книге Евклида, состоит в способе доказательства приведенных утверждений. Евклид в данном фрагменте представляет числа в виде отрезков, а Пифагор и его последователи пользовались счетными камешками (псефами). В остальном доказательства, приводимые Евклидом, скорее всего, сходны с доказательствами Пифагора. Интересно, что в восходящем к Пифагору фрагменте «Начал» для некоторых положений даже применяется такой метод, как доказательство от противного. Открытие этого метода также вполне можно приписать Пифагору.
Исследования свойств четных и нечетных чисел стали первыми исследованиями в области теории чисел. Таким образом, нашего героя с полным правом можно назвать основателем этого раздела математики.
Во времена Пифагора и, скорее всего, им самим, также была разработана теория фигурных чисел. Эта теория стала результатом попыток найти взаимосвязь между числами и геометрическими фигурами. Здесь следует несколько подробнее рассмотреть методы счета, используемые пифагорейцами. Для вычислений, как мы уже говорили, они использовали счетные камешки. Их выкладывали на песке, а позже — на счетной доске (абаке) в виде геометрических фигур. Кстати, некоторые источники приписывают изобретение абака Пифагору. Интересно, что при таком взгляде на числа невозможно было представить ноль. Даже единицу считали не числом, а «числовым атомом», а другие числа считали множеством единиц, что и нашло свое отображение в пифагорейской философии.
Рассматривая фигуры, которые образовывали выложенные на песке псефы, Пифагор обнаружил несколько типов фигурных чисел.
Квадратные числа — сумма ряда нечетных чисел, начиная с единицы: 1 + 3 + 5+… + (2n -1) = n2.
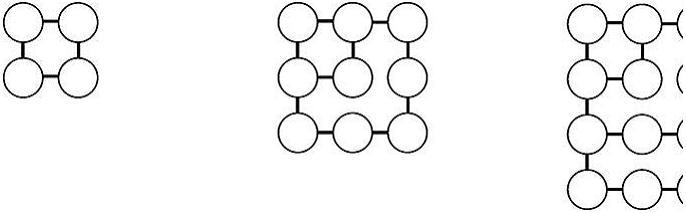
Прямоугольные числа - сумма четных чисел, начиная с 2: 2 + 4 + 6 +...
+ 2n = n (n
- 1).
Треугольные числа:
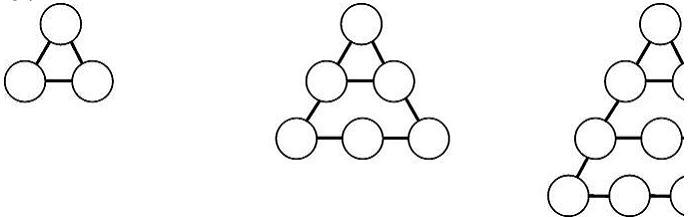
Телесные (объемные) числа:
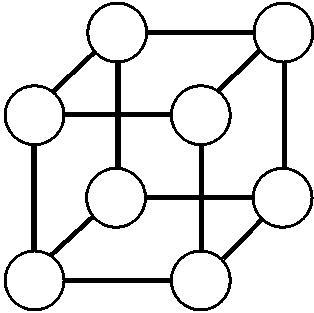
Простые (линейные) числа - те, которые можно было выложить только в виде линии.

На примере квадратных и прямоугольных чисел можно видеть, что с их помощью вполне могли быть открыты закономерности суммирования арифметических рядов.