Вернемся к постулату о параллельных, который дает нам весьма точный способ классификации поверхностей на плоские, сферические и гиперболические. Для любой заданной прямой и точки вне ее:
На плоской поверхности имеется одна и только одна параллельная прямая, проходящая через эту точку.
На сферической поверхности нет ни одной параллельной линии, проходящей через эту точку[71].
На гиперболической поверхности имеется бесконечно много параллельных линий, проходящих через эту точку.
Поведение параллельных линий на плоской или сферической поверхности можно понять интуитивно, потому что нам легко представить себе плоскую поверхность, которая продолжается до бесконечности, и потому что все мы знаем, что такое сфера. Гораздо более сложная задача — понять поведение параллельных линий на гиперболической поверхности, потому что совершенно не ясно, как будет выглядеть такая поверхность, когда она продолжается до бесконечности. Параллельные линии в гиперболическом пространстве расходятся все дальше и дальше друг от друга. При этом, отклоняясь одна от другой, они не изгибаются, потому что, раз мы говорим о параллельных линиях, они должны быть прямыми, и тем не менее они расходятся из-за того, что гиперболическая поверхность постоянно искривляется, уходя сама от себя, а по мере того, как поверхность расширяется, между любыми двумя параллельными линиями появляется все больше и больше места. Да уж, такая картина кого угодно сведет с ума, и неудивительно, что, несмотря на всю свою гениальность, Риман не сумел придумать никакой поверхности, которая имела бы заданные свойства.
В последние десятилетия XIX века проблема представления гиперболической плоскости возбуждала многих математиков. Одна из таких попыток, предпринятая Анри Пуанкаре, захватила воображение голландского художника-графика М. К. Эшера (1898–1972). Его знаменитая серия гравюр «Предел круга» возникла как результат знакомства с предложенной французским математиком «дисковой моделью» гиперболической поверхности. На гравюре «Предел круга IV» двумерная вселенная помещена на круг (диск), где ангелы и демоны уменьшаются по мере приближения к краю. Сами ангелы и демоны, однако, и не подозревают о том, что уменьшаются, потому что по мере того, как они сами становятся меньше, то же самое происходит и с их измерительными приборами. С точки зрения обитателей диска все они сохраняют свои размеры, а их вселенная продолжается до бесконечности.

«Предел круга IV»
Изобретательность, воплощенная в дисковой модели Пуанкаре, состоит в том, что она восхитительным образом иллюстрирует, как параллельные линии ведут себя в гиперболическом пространстве. Прежде всего, нам надо определиться с тем, что такое прямая линия на диске. Аналогично тому, как прямые на сфере линии выглядят искривленными, когда их изображают на плоской карте (например, маршруты самолетов являются прямыми, но на карте выглядят искривленными), линии, являющиеся прямыми в диско-мире, также кажутся нам искривленными. Пуанкаре определил прямую линию на диске как сечение диска окружностью, которая входит в него под прямым углом.
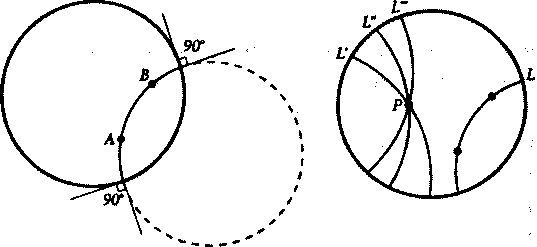
На левой картинке внизу изображена прямая линия между точками А и В, для нахождения положения которой надо построить окружность, проходящую через точки А и В и входящую в диск под прямым углом. Гиперболический вариант постулата о параллельных утверждает, что для каждой прямой L и точки P вне этой прямой имеется бесконечно много прямых, параллельных L, которые проходят через P. Это показано на рисунке внизу справа, где отмечено три прямых — L', L'' и L''', — которые проходят через точку P, но при этом все параллельны прямой L. Линии L', LL'' и L''' представляют собой части различных окружностей, которые входят в диск под прямыми углами. Глядя на рисунок, можно понять, как может получиться, что имеется бесконечно много прямых, параллельных L и проходящих через P, — просто потому, что можно нарисовать бесконечное число окружностей, которые входят в диск под прямыми углами и проходят через P. Модель Пуанкаре, кроме того, помогает нам понять смысл утверждения о том, что две параллельные линии расходятся: L и L' параллельны, но становятся все дальше и дальше друг от друга по мере приближения к краю диска.
Диско-мир Пуанкаре позволяет понять многое, но не все. При том что он снабжает нас концептуальной моделью гиперболического пространства, искаженного за счет взгляда через довольно странную линзу, он не показывает, как же гиперболическая поверхность будет выглядеть в нашем мире. Поиску более реалистичных гиперболических моделей — предприятию, которое подавало большие надежды в последние десятилетия XIX столетия, — нанес в 1901 году удар выдающийся немецкий математик Давид Гильберт (1862–1943): он доказал, что невозможно описать гиперболическую поверхность, используя какую-либо формулу. Математическое сообщество приняло доказательство Гильберта без энтузиазма, поскольку математики решили, что если нет никакого способа описать поверхность с помощью формулы, то, значит, такая поверхность и не существует. Интерес к производству моделей гиперболических поверхностей стал угасать.
Что и возвращает нас к Дайне Таймине, с которой я встретился в Лондоне на южном берегу Темзы, представляющем собой набережную-променад, вдоль которой располагаются театры, художественные галереи и кинотеатры. Она кратко напомнила мне историю гиперболических пространств — предмет, который она преподавала в качестве ассистента в Корнеллском университете. Из Гильбертова доказательства невозможности описания гиперболического пространства с помощью формулы, сообщила она мне, имелось следствие: компьютеры также оказались не в состоянии создавать образы гиперболических поверхностей, потому что компьютеры могут создавать только образы, основанные на формулах. Однако в 1970-х годах геометр Уильям Тёрстон (р. 1946) предложил подход, хоть и не основанный на высоких технологиях, но оказавшийся весьма плодотворным. Не обязательно обладать формулой для создания гиперболической модели, говорит Тёрстон, все, что требуется, — это бумага и ножницы. Тёрстон, которому в 1981 году была присуждена Филдсовская медаль (высшая награда для математика) и который теперь был коллегой Дайны в Корнеллском университете, предложил модель, состоявшую в соединении друг с другом бумажных кусочков, имеющих форму подковы.
Дайна использовала модель Тёрстона на занятиях со студентами, но модель оказалась столь хрупкой, что неизменно рассыпалась на части, и Дайне каждый раз приходилось делать новую. «Ненавижу склеивать бумагу. Это занятие сводит меня с ума», — жаловалась она. И тут ей пришла в голову свежая идея — что, если вместо бумаги попробовать связать модель гиперболической плоскости?
Идея ее была проста: наберем один ряд петель, а затем в каждом следующем ряду будем прибавлять некоторое заданное количество петель. Например, можно прибавлять по одной петле через каждые две. В таком случае, если мы начали с ряда из 20 петель, то во втором ряду их будет 30 (мы добавили 10), в третьем — 45 (мы добавили 15) и т. д. (В четвертом должно оказаться 22,5 дополнительные петли, но, поскольку полпетли связать невозможно, будем округлять до большего или меньшего их целого числа.) По замыслу Дайны должен был получиться кусок вязаного полотна, который будет становиться все шире и шире, как будто он гиперболически расширяется сам из себя. Однако вязание на спицах — дело довольно хлопотное, из-за одной ошибки порой приходится распускать весь ряд. Поэтому вместо спиц Дайна взяла вязальный крючок. Если вязать крючком, то легче исправить ошибку, потому что в процессе вязания на крючке всего одна петля. Так что она довольно быстро приноровилась. Помогла еще и настойчивость в овладении рукоделием — привычка, приобретенная в детстве, которое она провела в 1960-х годах в Латвии.
71
Можно было бы подумать, что линии постоянной широты параллельны экватору. Это не так, потому что линии широты (за исключением экватора) — это не прямые линии, а лишь прямые линии могут быть параллельны друг другу. Прямая — это кратчайшее расстояние между двумя точками; вот почему самолет, летящий из Нью-Йорка в Мадрид — при том, что эти две точки находятся на одной широте, — не летит по линии постоянной широты, а выбирает траекторию, которая на двумерной карте выглядит искривленной. (Примеч. авт.)