Например, посветили белым (солнечный свет), и все цвета, кроме желтого, поверхность поглотила — значит, видим желтую поверхность.
Если другая поверхность поглотит все цвета, кроме синего и красного (последние, соответственно, отразит), мы опять увидим желтую поверхность — вспомним: синий плюс красный видно как желтый.
Но вот если осветить первую поверхность с помощью света нашего светодиода, что мы увидим? Черную поверхность, ведь в составе света не было настоящего желтого — того, который наш предмет отражает! А вторую поверхность мы увидим такой же желтой, как и прежде, ведь синий и красный в нашем фонарике в наличии.
Что это означает? Неправильную цветопередачу. Светло-то светло, да ничего не видно. Если сделать из такой лампы яркую (уж это — пожалуйста!) автомобильную фару, то в свете таких фар вы рискуете не увидеть пешехода, переходящего дорогу перед вашим автомобилем.
Читатель может возразить: что-то я все-таки увижу. Ну, неправильные будут цвета, но дорога — не картинная галерея, как-нибудь разберемся. Ошибка, причем грубая! И вот почему.
Вспомните принцип маскирующего камуфляжа. Хотите, представьте форму солдата, хотите шкуру тигра или леопарда — принцип один. И дело опять в особенностях нашего зрения. Мы узнаем образ того, что мы видим по границе этого образа, так устроено наше зрение (глаза плюс мозги). Чтобы «увидеть», достаточно одной границы: вспомните замечательные карикатуры Херлуфа Битструпа — ничего, кроме контура, но все узнаваемо. А вот если контур убрать, а именно это делают камуфлирующие пятна или полосы, увиденное сольется с фоном. При неправильной цветопередаче велик риск того, что контур распадется, — перед глазами будут не воспринимаемые нами «камуфляжные» пятна. Вот так: проверили фонарик — светит хорошо, ярко; посветили — и ничего не увидели!
Но наш главный риск не в том, что мы в неверном освещении проглядим что-то важное. Наш главный риск — не увидеть те сюрпризы, которые таит в себе все новое. И не надо полагаться на очевидность — она-то и подведет, особенно в области нано.
Риск применения нанотехнологий по внетехнологическим причинам.
Риск технологической подмены — замещающая нанотехнология несет те же риски, что и замещаемая.
Риск неправильной цветопередачи как пример риска искажения восприятия.
Риск очевидности — не надо полагаться на очевидность — она-то и подведет.
Глава 2
Чудеса структуры
2.1. Фрактальная симфония
— Разрешите доложить, капитан: полный штиль, барометр показывает ясно, температура наружного воздуха двенадцать градусов по Цельсию, произвести измерение глубины и температуры воды не представилось возможным за отсутствием таковой.
… — То есть как это за «отсутствием»? — спрашиваю. — Куда же она девалась?
В предыдущей главе мы говорили о материалах и о рисках, с ними связанных. Было отмечено, что все начинается с материала. Однако последние примеры (со сверхпроводимостью, с материалами для водородной энергетики) показали, что важнейшим в материалах была их структура. Нанотехнологии — это тот случай, когда материал уходит на второй план, а на первый план выходит структура.
Действительно, мы не просто имеем дело с атомами — с ними мы имеем дело всегда, ведь из них состоят самые привычные вещи, — мы эти атомы размещаем так, как нам необходимо. Такое размещение и есть структура. При этом структура нано часто особенная. В привычном нам кристалле, например соли, тоже есть четкая структура — бесконечная череда повторяющейся во все стороны кристаллической решетки. Но не о такой «монотонной» структуре речь. Структуры нано более сложные.
Показательным примером такой особенной структуры являются так называемые дендримеры. Это как раз тот материал, который применяется для «губок» водородной энергетики.
Дендример — название говорящее. Это макромолекула, похожая на дерево[25], точнее на его крону. Только подобия в дендримере еще больше — в кроне дерева ветки разные: ближе к стволу — толще, дальше от ствола — тоньше; в дендримере все веточки одинаковые и структура — строго регулярная (рис. 2.1).
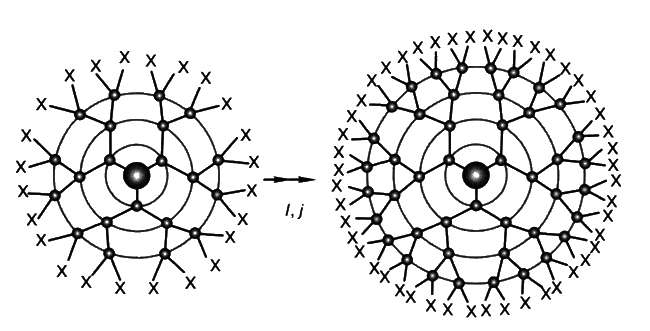
«Ну и что, — скажет читатель. — В чем же особенность такой структуры? Похожа на кристалл, только немного странный». Странный — да, но не немного!
Дендример — фрактал. Хоть фракталы часто встречаются в нашей жизни, то, что они не такие, как обычные тела, поняли относительно недавно. Считается, что самым первым примером фрактала была береговая линия острова. Бенуа Мандельброт[27] в 1967 г. задался вопросом: какова длина береговой линии, например, острова Великобритания[28]? Взял карту и измерил. Получил результат. Ему бы на этом успокоиться, но он взял карту большего масштаба, т. е. подробнее. Измерил. Результат получился другой — линия оказалась много длиннее! Тогда Мандельброт взял карту еще большего масштаба, еще более подробную. И опять длина линии здорово увеличилась. Ученый задумался: что же получается — у линии нет длины? Действительно, чем подробнее будет карта, тем больший результат мы получим. И никакой из результатов изменений, даже последний, не будет верным, потому что можно взять карту еще подробнее.
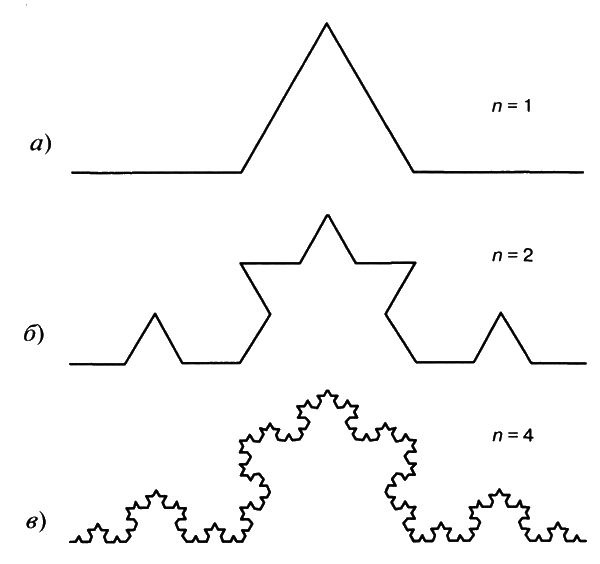
Чтобы это понять, рассмотрим кривую под названием кривая Коха[29]. Такая кривая строится так, как на рис. 2.2.
Сначала кривая выглядит как на рис. 2.2, а. Она состоит из четырех одинаковых прямых. По краям (первая и последняя трети) — прямые, а в средней трети две прямые, соединенные «треугольником». Длина такой кривой — 4/3, если за единицу принять длину основания кривой. Теперь давайте заменим каждую из четырех прямых линий на такую же, но уменьшенную в масштабе. Получится как на рис. 2.2, б. Длина линии составит (4/3)2. Можно продолжать процесс замены прямых на уменьшенную кривую. На следующей стадии замены (рис. 2.2, в) линия будет более изрезанной, а длина ее составит (4/3)3 на следующей стадии — (4/3)4. И так без конца. Длина линии бесконечна. Чем больше мы ее дробим, тем она длиннее. А теперь представьте, что мы рассматриваем эту кривую, нарисованную на карте. Мелких деталей не видно — длина кривой конечна. Но вот мы взяли карту с лучшим разрешением — и детали проявились. И длина увеличилась. Если разрешение увеличить втрое, проявится следующая часть структуры кривой, ведь так мы ее строили — каждый шаг связан с уменьшением масштаба втрое. А длина кривой на карте (в увеличенном масштабе) увеличится в 4 раза (4/3×3). Если увеличить масштаб карты в 3 или 10 раз, то длина обычной, привычной нам кривой увеличится также — соответственно в 3 или 10 раз. А для фрактала это не так! При изменении масштаба в k раз наблюдаемая длина нашего фрактала увеличится в k4/3 раз. Для обычной кривой — в k1 раз. Эта маленькая единичка и есть размерность обычной кривой — она одномерна.
Для площади наш показатель был бы равен двойке. Если линейные размеры увеличить в k раз, то площадь увеличится в k2 раз. Для объема — показатель 3. Двойка и тройка — размерность (соответственно) площади и объема. А наш фрактал имеет дробную размерность — 4/3 [31]. Он, конечно, не плоскость, но уже и не линия! Фракталы-линии бывают разные. И размерности у них тоже разные — между единицей и двойкой.
25
Дендримеры — древообразные полимеры (от греч. dendron — дерево), молекулы которых имеют большое число разветвлений.
26
27
Бенуа Мандельброт (1924–2010) — французский и американский математик, создатель фрактальной геометрии.
28
Mandelbrot В. How long is the coast of Britain? Statistical self-similarity and fractional dimension // Science. New Series. Vol. 156, No. 3775 (May 5, 1967). 636–638.
29
Нильс Фабиан Хельге фон Кох — шведский математик.
30
Koch H. von. Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire // Archiv for Matemat., Astron. och Fys. 1904. 1681–702;
Koch H. von. Une méthode géométrique élémentaire pour l’étude de certaines questions de la théorie des courbes planes // Acta Math. 1906. 30 145–174.
31
Математик здесь нас обязательно поправит. Он скажет, что размерность, добавив слово Хаусдорфова, равна ln 4 / ln 3 = 1,26. Но давайте, каждый раз произнося слово «размерность», будем иметь в виду «степень подобия», и все встанет на свои места.