
Бегун. Прежде чем я преодолею последнюю четверть дистанции, мне необходимо пробежать ее половину. И так всякий раз. Прежде чем преодолеть какое-то расстояние, мне необходимо пробежать половину его. Этим половинам не будет конца! Я никогда не доберусь до финиша!
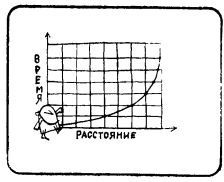
Предположим, что на преодоление половины каждого расстояния бегун затрачивает 1 мин. На графике зависимости времени от пути видно, что бегун приближается к финишу, но так и не достигает его. Правильны ли рассуждения бегуна?
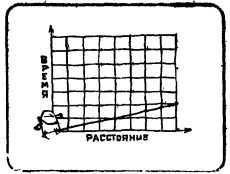
Нет, неправильны: бегун не затрачивает по 1 мин на преодоление половины каждого отрезка. Каждую половину очередного отрезка он пробегает за вдвое меньшее время, чем половину предыдущего отрезка. Бегун достигнет финиша через 2 мин после старта, хотя ему придется за эти 2 мин преодолеть бесконечно много половин соответствующих отрезков дистанции.
Зенону принадлежит и другой, не менее знаменитый парадокс об Ахилле и черепахе. Быстроногий Ахилл хочет поймать черепаху, которая находится на расстоянии 1 км от него.
К тому времени, когда Ахилл добегает до того места, где первоначально находилась черепаха, та успевает уползти вперед на 10 м.
За то время, которое требуется Ахиллу, чтобы пробежать эти 10 м, черепаха снова успевает уползти на какое-то расстояние.
Черепаха. Где тебе догнать меня, старина! Каждый раз, когда ты добежишь до того места, где я была, я успею уползти на какое-то расстояние вперед, хоть на толщину волоса!
Зенон, разумеется, знал, что Ахилл мог бы поймать черепаху. Свои парадоксы Зенон придумал для того, чтобы показать, к каким парадоксальным следствиям приводит представление о неделимых — «атомах» — пространства и времени, имеющих сколь угодно малые, но конечные размеры.
B обоих парадоксах Зенона бегунов следует считать точками, движущимися с постоянной скоростью вдоль прямой. Зенон знал, что если отрезок АВ имеет конечную длину, то точка, движущаяся из А в В с конечной скоростью, достигает финиша за конечное время. Свои парадоксы Зенон придумал для того, чтобы продемонстрировать, к каким трудностям приводят атомистические представления о структуре пространства и времени, согласно которым отрезок «рассыпается» на отдельные неделимые элементарные отрезки, нанизанные один за другим, наподобие бусин, а время— на отдельные неделимые промежутки (и элементарным отрезкам» и элементарным промежуткам времени атомисты приписывали конечную протяженность).
Доказать, что бегун достигнет финиша (точки В) за конечное время, поскольку на преодоление половины очередного отрезка дистанции ему потребуется вдвое меньше времени, чем на преодоление половины предыдущего отрезка (как это сделали мы), еще не означает решить парадоксы Зенона. Услышав о нашем решении, Зенон возразил бы, что, подобно тому как, прежде чем преодолеть любое расстояние, бегун сначала должен преодолеть половину этого расстояния, прежде чем истечет какой-то промежуток времени, должен истечь вдвое меньший промежуток времени.
Иначе говоря, все, что Зенон говорит о прямой, в равной мере применимо и к временной последовательности событий. Время, затрачиваемое бегуном на преодоление дистанции, будет все более приближаться к 2 мин, но до истечения 2 мин всегда будет оставаться бесконечное число мгновений («неделимых» по терминологии атомистов). To же относится и к парадоксу об Ахилле и черепахе. На каждом этапе бесконечного процесса преследования черепахи быстроногим Ахиллом впереди — и в пространстве, и во времени — неизменно будет оставаться бесконечно много «следующих» этапов.
Многие специалисты согласились со знаменитым анализом парадоксов Зенона, данным Бертраном Расселом. По мнению Рассела, парадоксы Зенона не были удовлетворительно решены вплоть до появления теории бесконечных множеств Георга Кантора.
Теория Кантора позволяет рассматривать бесконечные множества (будь то множества точек на прямой или мгновений времени) не как набор изолированных индивидуальных точек и событий, а как нечто целое. Суть парадоксов Зенона и состоит как раз в том, что ни пространственные отрезки, ни временные промежутки недопустимо рассматривать как состоящие из бесконечно большого числа дискретных членов, изолированных друг от друга, как следы на снегу. Решение парадоксов Зенона требует теории типа канторовской теории множеств, в которой наши интуитивные представления об отдельных точках и индивидуальных событиях объединены в систему — последовательную теорию бесконечных множеств.
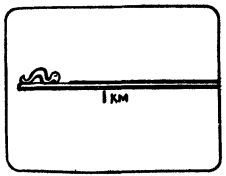
А вот совсем новый парадокс, о котором не знал Зенон. На одном конце резинового каната находится червяк. Длина каната — 1 км.
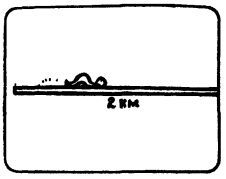
Червяк ползет по канату с постоянной скоростью 1 см/с. Через 1 с после того, как червяк пустился в путь, канат растянули, и его длина стала равной 2 км. Через 2 с канат снова растянули, и его длина достигла 3 км. Каждую следующую секунду канат удлиняется на 1 км. Доползет ли червяк когда-нибудь до конца каната?
Ваша интуиция подсказывает вам, что червяк никогда не доползет до конца каната, но он все же доползет! Доползет-то доползет, но когда?
Задача легко решается, если учесть, что канат растягивается равномерно, как резиновая лента. Следовательно, при каждом растяжении червяк переезжает вперед — его переносит на себе, растягиваясь, сам канат.
Путь, пройденный червяком за каждую секунду, удобно выражать в долях длины каната к концу той же секунды. Как только сумма дробей, выражающих эти доли, станет равной 1, червяк достигнет конца каната.
В одном километре 100000 см, поэтому за первую секунду червяк преодолеет 1/100000 длины каната. За вторую секунду червяк проползет еще 1 см, что составляет 1/200000 от новой длины каната, которая достигнет уже 2 км. За третью секунду червяк проползает еще 1 см, что составляет 1/300000 от длины каната, которая к этому времени достигнет 3 км, и т. д. По истечении k секунд червяк проползет расстояние, составляющее от «текущей» длины каната долю, которая представима в виде
В скобках стоит сумма первых k членов так называемого гармонического ряда. Заметим, что сумма членов, заключенных между 1/2 и 1/4, включая 1/4, то есть 1/3 + 1/4 больше, чем 2 х 1/4 = 1/2. Аналогично сумма членов, заключенных между 1/4 и 1/8, включая 1/8, то есть 1/5 + 1/6 + 1/7 + 1/8, больше, чем 4 х 1/8 = 1/2. Следовательно, сумма членов ряда, заключенных между 1/1 и 1/2k, включая 1/2k, всегда больше, чем k x 1/2 = k/2 в чем нетрудно убедиться, если члены сгруппировать: возьмите сначала сумму двух первых членов, затем сумму следующих восьми членов и т. д.