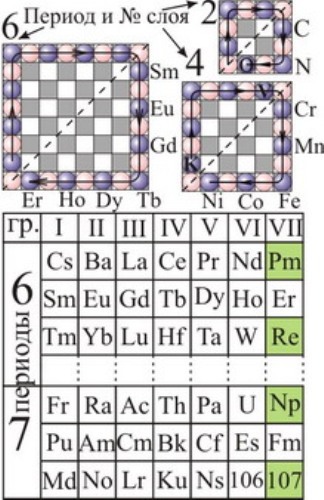
Рис. 109. Расположение лантаноидов и актиноидов в таблице Менделеева по Браунеру и Прандтлю с соответствующим порядком заполнения электронами слоёв 6-го и других чётных периодов.
Другое важное свойство этой формы таблицы в том, что она позволяет выделить элементы с ферромагнитными свойствами. Если рассмотрим элементы второй строки 6-го периода — Sm, Eu, Gd, Tb, Dy, Ho, Er, то увидим, что или они сами, или их соединения — сильные ферромагнетики. Такое подразделение сразу позволяет выявить уникальные элементы с ферромагнитными свойствами и в других чётных периодах таблицы. Так, во втором периоде периметр слоя содержит 6 электронов. Разделяя их и соответствующие элементы на две равных группы и беря элементы из второй, — C, N, O, найдём, что именно их соединения обладают ферромагнитными свойствами. То же, и в четвёртом периоде, где периметр слоя содержит 10 электронов, вторая половина соответствующих элементов — Cr, Mn, Fe, Co, Ni (Рис. 109) — либо сами, либо в соединениях, — яркие ферромагнетики. Итак, пирамидальная модель сразу выделяет те редкие элементы, что наделены ферромагнитными свойствами. По сути, это атомы, в которых идёт заполнение мест возле граней правого отсека нижней пирамиды (Рис. 104, Рис. 107). А элементы, у которых идёт заполнение электронами мест в углах пирамиды у краёв перегородки (Cr, Ti, Nd, Er, Tm, Yb), обладают уникальными оптическими свойствами, находя применение в качестве активных ионов в лазерах.
То же, что у лантаноидов, построение таблицы применимо и к 7-му периоду, содержащему актиноиды (Рис. 109). Таблица и пирамидальная модель атома снова объясняют, почему многие актиноиды проявляют, вместо 3-ей, — нетипичные для себя валентности: Md — (+I); No — (+II); Th, Bk — (+IV); Pa — (+V); U — (+VI); Np — (+VII) [145], чего не может объяснить квантовая физика. Не случайно, давно уже замечено, что актиноиды, в отличие от лантаноидов и вопреки предсказаниям квантовой теории атома, очень мало похожи друг на друга. Например, уран химически больше напоминает не своих "собратьев" из 3-й группы, а металл вольфрам из 6-й группы. Так что помещение актиноидов, равно как и лантаноидов, в одну клетку таблицы Менделеева многие считают условным и даже ошибочным [13].
Ещё на заре становления учения о строении атома такие учёные, как Томсон, Льюис, Ленгмюр, Ленард, Ритц, разработали модели атома в форме геометрически правильных тел, образованных упорядоченно размещёнными субатомными частицами, чем объяснили многие атомные свойства [49]. Такая кристаллическая модель атома была не только проста, наглядна, но и наиболее естественна, ибо стандартные числа электронов на атомных уровнях, точная идентичность однотипных атомов и их спектров наводят на мысль о кристаллах и правильных геометрических телах. Но с приходом квантовой механики эти модели забыли, хоть они и объясняли эффекты загадочные для квантовой физики. Бипирамидальная кристаллическая модель позволит не только наглядно и классически истолковать все свойства атомов и ядер, глубже понять суть таблицы Менделеева, но и открыть новые закономерности и свойства элементов, научиться находить новые соединения с заданными свойствами, включая ферромагнитные сплавы, полупроводниковые материалы, высокотемпературные сверхпроводники (§ 5.9). Квантовая же теория объясняет, по большей части, лишь уже известные свойства, да и то ограниченно.В своём стремлении спасти ошибочную планетарную модель атома, творцы квантовой физики, во главе с Бором, предпочли уничтожить механику, нежели отказаться от своего идола. А идеи Ритца, Дж. Томсона, Ленарда, Льюиса, Лэнгмюра, Циолковского, которые пытались построить альтернативную модель атома, в рамках классической механики, были отвергнуты и забыты. В итоге, вот уже век наука не имеет ясных представлений о структуре атома и ядра.
§ 3.4 Спектры щелочных металлов, сложных атомов и молекул
Комбинируя путём сложения или вычитания, либо сами сериальные формулы, либо входящие в них константы, можно построить новые формулы, которые позволяют полностью вычислить новые линии щелочных металлов, открытые за последние годы Ленардом и другими, а также делают возможными далеко идущие приложения к другим элементам, в частности к гелию.
Выше был объяснён на основе модели атома Ритца спектр водорода и водородоподобных атомов, а также рентгеновские спектры и закон Мозли для них (§ 3.2). Но Ритц нашёл объяснение также и спектрам более сложных атомов, например атомов щелочных металлов. Их спектры имеют гораздо более сложную структуру, чем у водорода и водородоподобных атомов. Как говорилось, это связано с влиянием полей дополнительных электронов на электрон, генерирующий спектр. Поскольку генерировать спектр может любой электрон, приведённый в колебательное движение, то усложнение спектра связано с общим взаимным влиянием электронов. Своими полями они смещают друг друга от прежних положений равновесия в новые, с иным значением поля Bи частоты колебаний в нём. Причём, поскольку все эти электроны могут занимать в атоме разные узлы, образуя разные конфигурации, то и смещения от положений равновесия, приводящие к изменению магнитного поля, могут быть различными и происходить в разные стороны. Соответственно, возникают дополнительные спектральные линии, генерируемые электронами в смещённых положениях: спектр атома обогащается, усложняется. И, чем больше электронов способно перемещаться в атоме, тем сложнее будет спектр.
Действительно, самыми простыми спектрами обладают щелочные металлы, стоящие в начале периодов, — в первой группе. Это означает, что в них имеется, по сути, один свободно смещающийся электрон. Все же остальные электроны прочно связаны в целиком заполненных электронных слоях (§ 3.3), а потому они вносят лишь небольшие стандартные искажения спектра. Вот почему спектры щелочных металлов очень напоминают водородный спектр, подчиняясь почти тем же зависимостям [74]. Элементы второй группы имеют уже два свободно смещающихся электрона, которые могут образовывать гораздо больше комбинаций положений в атоме, соответственно, и спектр этих элементов сложнее. И так далее: чем больше электронов, тем сильней усложняется спектр, если только новые электроны не образуют устойчивых симметричных конфигураций и не окажутся прочно связаны в слое, скажем, — вдоль его периметра. Впрочем, с приближением к концу периода, когда свободных мест остаётся всё меньше, электроны всё неохотней отрываются от слоя и образуют меньше разных комбинаций, поэтому, к концу периода спектр может даже упрощаться. Наконец, у инертных газов, где все электроны должны быть прочно связаны в слое (Рис. 106), необходимо отделение одного или нескольких электронов от слоя — для генерации спектра на электронном уголке. Это объясняет связь характера спектра с положением элемента в таблице Менделеева, с его химическими свойствами. А именно: число электронов, которые может отдать или принять атом для образования химической связи, задаёт также число электронов, способных переходить из крайнего электронного слоя в плоскость, где происходит генерация спектра (Рис. 107), с образованием там разных конфигураций и усложнением спектра взаимным влиянием.
Объясняет взаимодействие электронов и то, почему многие из сложных атомов имеют мультиплетный спектр: каждая спектральная линия окружена близкими линиями-спутниками. Вероятно, причина этого в том, что внутриатомные электрические поля остальных электронов слегка смещают генерирующий электрон от равновесного положения. Соответственно, меняется магнитное поле возле электрона и генерируемая его колебаниями частота линии. Разным положениям окружающих электронов в атоме отвечают разные позиции генерирующего электрона возле узла. А, потому, вместо одной линии в сложных атомах мы наблюдаем группу близко расположенных линий, за каждую из которых отвечают свои атомы. Интенсивность линии определяется процентом атомов, её генерирующих, то есть, — вероятностью для электронов занять соответствующие положения в атоме [104]. Поэтому, как показал ещё Ритц, чем ближе к границе серии, то есть, — чем выше mв формуле f= Rc[1/ n 2–1/ m 2] и чем дальше электрон от оси и начала координат, тем ниже интенсивность линии, поскольку электрону сложнее удержаться в дальних узлах. По той же причине, линии становятся всё более размытыми: электроны и позитроны в остове дрожат за счёт теплового движения, как атомы в простом кристалле (§ 3.14). Чем дальше электрон, тем сильней это сказывается, и тем его положение всё менее стабильно, соответственно, — и линии более размыты [104].