Перечислим оставшиеся три силы инерции:
Сила Кориолиса:
F 2= - 2mwv
сила, возникающая при ускоренном вращении
F 3= - mer,
где e- угловое ускорение;
и, наконец, поступательная сила инерции:
F 4= - mW ,
где W - поступательное ускорение.
Поступательная сила инерции возникает при ускоренном поступательном движении. Например, вы сидите в кресле самолета и он начинает разгоняться для взлета. Вы чувствуете как вас вдавливает в кресло некая сила. Это и есть действие поступательной силы инерции. Казалось бы, какое отношение к вращению имеет поступательная сила инерции, если она возникает при поступательном ускорении? Тем не менее, с точки зрения четырехмерного пространства событий поступательное ускорение тоже есть вращение, но вращение в пространственно-временных плоскостях (см. рис. 3).
Физики экспериментально установили, что силы инерции действуют только в ускоренных системах отсчета. С помощью преобразований координат, которые соответствуют переходу из ускоренной системы отсчета в инерциальную, силы инерции обращаются в нуль. Таким образом, силы инерции имеют относительную природу.Это их свойство заставляет некоторых исследователей считать их нереальными. Дело доходит до курьеза. В одном из технологических университетов студентам читают лекцию по теоретической механике и говорят, что силы инерции фиктивны, поскольку их можно обратить в нуль преобразованиями координат. Их удобно использовать в ускоренных системах отсчета для решения некоторых задач. Через некоторое время студентам читают лекцию по деталям машин, где рассматривают устройство турбины реактивного двигателя, которая вращается с большой угловой скоростью. При этом говорят, что если не учесть возникающих при вращении турбины сил инерции, то при недостаточной прочности металла они могут разорвать ее лопасти. Бедные студенты! Они никак не возьмут в толк, как это фиктивные силы могут разорвать металлические детали турбины.
Безусловно, силы инерции надо рассматривать как реальные. Но порождены эти силы особыми полями - полями инерции. Эти поля можно рассматривать как проявление торсионных полей в нашей повседневной жизни.
Если в инерциальных системах отсчета силы инерции обращаются в нуль, то, как оказалось, порождающие их поля инерции в инерциальных системах отличны от нуля.Такое в физике обнаружено впервые. Обычно обращение, например, гравитационной силы в нуль означает равенство нулю гравитационного поля, которое порождает эту силу. Это правило выполняется и для других физических полей. Поля инерции представляют собой разновидность торсионного поля, для которых обращение в нуль вызванных им сил не означает равенства нулю самого поля.
Поле инерции может быть обращено в нуль с помощью преобразований вращательных координат. Это наглядно видно из формулы Френе w = cv, которая устанавливает связь между угловой частотой вращения wи кручением c(одной из компонент торсионного поля). Выбирая вращательные координаты так, чтобы, w=0, мы обращаем в нуль кручение c(т.е. поле инерции). Следовательно, поле инерции относительно, поскольку всегда можно найти систему отсчета, где оно оказывается равным нулю.
1.12. Три вида пространств Вайценбека.
Введение вращательной относительности в физику позволило обнаружить новые физические поля, названные торсионными. Эти поля наблюдаются во вращающихся системах отсчета. Как было отмечено ранее, пространство событий относительных координат вращающихся систем отсчета (ускоренных локально инерциальных систем второго рода) имеет структуру геометрии Вайценбека. В общем случае пространство Вайценбека обладает отличной от нуля римановой кривизной и кручением, введенным впервые итальянским математиком Риччи. Одной из компонент кручения Риччи является рассмотренное нами ранее кручение Френе c. Пространство Вайценбека (в математике оно иногда называется пространством абсолютного параллелизма)устроено таким образом, что в общем случае кручение пространства выступает как источник римановой кривизны (см. рис. 13 в).
Простейшим пространством абсолютного параллелизма является трехмерное пространство Евклида или четырехмерное псевдоевклидово пространство. Кручение и кривизна этих пространств равна нулю, поскольку они описывают абсолютный вакуум (см. рис. 13 а).
Напомним, что пространство событий относительных координат инерциальных систем отсчета обладает структурой пространства Евклида (трехмерный случай) или псевдоевклидова пространства (четырехмерный случай).
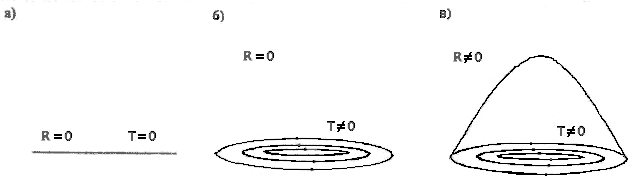
Рис. 13. Различные виды пространств абсолютного параллелизма: а) плоское пространство (риманова кривизна Rи кручение Риччи Травны нулю), б) пространство с нулевой римановой кривизной Rи отличным от нуля кручением Риччи Т; в) пространство с не нулевой римановой кривизной Rи не нулевым кручением Т.
Эти пространства представляют собой простейший вид геометрии абсолютного параллелизма и не несут какой-либо содержательной физической информации.
Рассмотрим теперь ситуацию, когда отсутствуют все поля кроме полей инерции. Можно, например, рассмотреть пространство событий относительных координат ускоренных локально инерциальных систем отсчета второго рода (см. рис. 11).Конечно, мы рассматриваем идеальный случай, когда гравитационным, электромагнитным и другими полями тела отсчета (в данном случае диска) можно пренебречь. Тогда риманова кривизна пространства событий оказывается равной нулю. В результате мы получаем пространство событий со структурой геометрии абсолютного параллелизма, у которой кручение Риччи отлично от нуля, а риманова кривизна равна нулю (см. рис. 13 б).
В отличие от бессодержательной плоской геометрии, соответствующей абсолютному вакууму, эта геометрия наделена структурой, которая описывает некие первоначальные вихри (или первоначально возбужденный вакуум).Теперь у нас появляются содержательные уравнения, которым подчиняются первичные торсионные поля, не создающие риманова искривления пространства, но приводящие к его закрутке. Искривление пространства связано с появлением силовых полей, т.е. таких полей, которые порождают силы, создающие кривизну траекторий частиц в инерциальных системах отсчета. Первичные торсионные поля действуют на частицы так, что их траектория не искривляется, при этом меняются вращательные свойства материи. Например, взаимодействие спинирующей
Самый общий случай геометрии Вайценбека соответствует пространству событий относительных координат ускоренных локально инерциальных систем отсчета первого и второго рода, т.е. фактически произвольно ускоренных систем. В этом случае, как риманова кривизна, так и кручение Риччи отличны от нуля (см. рис. 13 в).
Перечислим некоторые важные свойства пространства Вайценбека:
а) для случая четырехмерных систем отсчета размерность этого пространства равна десяти;
б) в пространстве существуют две метрики - метрика Римана, описывающая бесконечно малое расстояние между двумя точками, и метрика Киллинга-Картана, представляющая собой поворот на бесконечно малый угол. Эта метрика исчезает, если кручение Риччи пространства обращается в нуль;