Поверхность раздела как тормоз для трещин
В вопросе о вязкости армированных пластиков, среди которых наиболее известны стеклопластики, существует интересный парадокс. Стеклопластик содержит множество тонких стеклянных волокон, склеенных смолой воедино. Стекловолокно не отличается от обычного стекла ни физически, ни химически. Как мы уже видели, стекла катастрофически хрупки; так же ведут себя и волокна из стекла. Более того, смола, которая используется как связующая матрица в стеклопластиках, также достаточно хрупка; может быть, почти в такой степени, как стекло. Однако, когда оба этих компонента объединены вместе, получается материал, который производится в больших количествах главным образом благодаря его вязкости.
Не так давно мы с Дж. Куком решили разобраться в этом явлении количественно. В материаловедении многие задачи связаны с математическими трудностями, теоретически разрешимыми, но требующими слишком трудоемкой вычислительной работы. К таким задачам относится в какой-то мере и расчет распределения напряжений вокруг трещины. Но мы должны знать некоторые особенности картины напряжений вокруг трещины, если хотим предугадать, как поведет себя трещина, столкнувшись на своем пути с какой-либо неоднородностью. Ведь стеклопластик - материал явно неоднородный, особенно интересная неоднородность возникает на границе раздела между волокном и смолой.
В наше время ЭВМ меняют все представления о вычислительных трудностях. Концентрация напряжений у кончика трещины была впервые вычислена Инглисом в 1913 году. Мы уже говорили об этом, его результаты можно считать классикой, они абсолютно верны. С тех пор целый ряд ученых, более способных, чем мы, работали над этой проблемой. Но дьявольски громоздкий математический аппарат одних заставлял предполагать, что кончик трещины бесконечно остер, то есть имеет нулевой радиус; тех же, кто считался с конечным радиусом головки трещины, та же самая математика принуждала использовать очень приближенные методы или же определять картину напряженного состояния только в какой-то ограниченной области. Предположение о бесконечно острой трещине ведет к бесконечно большим напряжениям, что, очевидно, лишено реального смысла и не помогает в решении проблемы разрушения[30].
Приближенные методы, использовавшиеся для случая конечного радиуса головки, не давали достаточно полного представления о том, что делается у самого кончика трещины, то есть там, где идет разрушение.
Как бы то ни было, с электронно-вычислительной машиной или без оной, я, вероятно, не смог бы управиться со всей этой математикой, но Куку нравятся такого рода упражнения, и, использовав вычислительную машину “Меркурий”, он сумел определить напряжения очень близко к кончику трещины с конечным радиусом.
Общая картина напоминает картину, показанную на рис. 18. Немного обобщая ее, мы могли бы изобразить траектории напряжений, то есть направления, по которым напряжения передаются с одной атомной связи на другую, как это сделано на рис. 30. Эта схема поможет нам понять детали картины напряжений, полученной Куком.
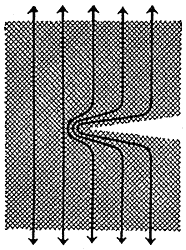
Рис. 30. Грубая схема траекторий напряжений в равномерно растянутом стержне, содержащем трещину.
Мы, конечно, понимали, что делаем два допущения, которые упрощают нашу задачу. Во-первых, мы считали, что кончик трещины имеет очертания эллипса или круга - на самом деле в материале, состоящем из атомов, такого быть не может. Во-вторых, мы предполагали, что материал ведет себя как сплошное упругое тело и подчиняется при этом закону Гука - это тоже не учитывает реальных особенностей материала. Но ничего лучшего мы предположить не могли, остается лишь надеяться, что ошибки, вызванные таким огрублением действительной картины, будут не слишком велики.
Первый вывод относительно распределения напряжений в области конца трещины, который Кук сделал из своих упражнений с ЭВМ, заключается в том, что не так уж важно, как приложена внешняя нагрузка. Конечно, общая картина напряженного состояния в теле будет сильно зависеть от того, каким способом мы вынудим трещину расти - будем ли мы расклинивать ее, например, гвоздем или зубилом или приложим растягивающую либо изгибающую нагрузку к телу, содержащему трещину. Но распределение напряжений в области, в которой развивается разрушение, то есть на расстоянии нескольких атомных размеров от кончика трещины, будет во всех случаях примерно одним и тем же. Следовательно, механизм разрушения не должен, по-видимому, зависеть от способа нагружения тела. Задача, таким образом, упростилась, а это уже означало некоторый шаг вперед.
Обратимся теперь к рис. 31 и 32, на которых изображены действительные картины напряжений, рассчитанные для трещины длиной 2 мкм и радиусом кончика 1А. Часть трещины, прилегающая к ее кончику, отмечена на рисунке штриховкой. Кривые линии проходят через точки тела, в которых коэффициент концентрации остается постоянным для напряжении, направленных по вертикали (рис. 31) и по горизонтали (рис. 32) в плоскости листа. (Заметьте, это - не траектории напряжений!) Число у каждой линии обозначает величину коэффициента концентрации, то есть число К, на которое следует умножить величину среднего напряжения на значительном удалении от трещины, чтобы получить соответствующее напряжение в любой точке на заданной линии. Когда размер трещины увеличивается, радиус ее кончика не изменяется; следовательно, концентрация напряжений возрастает. Но характер распределения напряжений остается прежним, все изменяется пропорционально. Для случая, когда трещина укорачивается, справедливо, конечно, обратное.
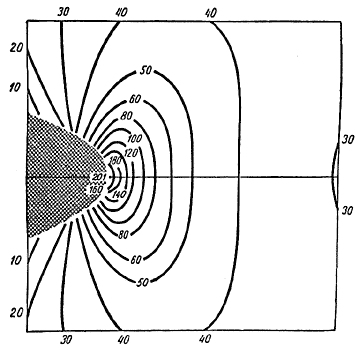
Рис. 31. Концентрация напряжении вблизи кончика эллиптической трещины.
Растягивающие напряжения направлены под прямым углом к трещине, то есть параллельно приложенной нагрузке. Заштрихованная область представляет собой трещину. Вдоль кривых коэффициенты концентрации постоянны, числа, проставленные на них, показывают, таким образом, во сколько раз местное напряжение превышает среднее по образцу. Максимальная величина концентрации - около 200. Абсолютная величина концентрации зависит от длины трещины, но пропорции остаются неизменными.
Из рис. 31 видно, что напряжения, направленные вертикально, то есть силы, стремящиеся раскрыть трещину, разорвать ее, очень велики, особенно в области, вплотную примыкающей к кончику трещины. Самые опасные напряжения приходятся на область, примерно равную площади одной атомной связи. Численная величина максимального напряжения равна здесь полученному Инглисом напряжению в самой крайней точке трещины (правда, это точное значение не столь уж важно, потому что все подобные расчеты основаны на каких-то допущениях). Но если мы продвинемся вперед от трещины, перескочим, грубо говоря, на следующую атомную связь, то обнаружим, что напряжение на ней упало в два с лишним раза по сравнению с максимальной величиной. Вероятно, эти соотношения верны всегда, и они очень ясно показывают, что большая часть нагрузки концентрируется в материале на единственной цепочке атомных связей, проходящей через самый кончик острой трещины; следует лишь помнить, что мы имеем дело с твердым телом (а не с листом бумаги) и кончик трещины представляет собой линию в трехмерном пространстве. Как только перегруженная связь на кончике трещины лопнет, пик концентрации напряжений переместится на следующую связь и т.д. и т.д., подобно петлям на чулке.
Если увеличивать только прочность химических связей, то это мало повлияет на прочность тела, содержащего дефекты, так как этот путь не уменьшает концентрации напряжений у трещин. Именно поэтому алмаз и сапфир - вещества хрупкие и обычно не очень прочные, несмотря на их большую твердость и высокую энергию химических связей. На этом можно было бы и поставить точку в истории о прочности и хрупкости, если бы дело ограничивалось более или менее упругими и более или менее однородными телами. С такой точки зрения практически безразлично, с какого рода телом мы имеем дело - кристаллическим, стеклообразным или даже полимером; несущественна и величина модуля Юнга. Важно лишь, чтобы тело подчинялось закону Гука в достаточно широкой области деформаций, вплоть до разрушения. Хрупкость - не есть особое состояние, она является нормальным состоянием всех простых твердых тел.