Можно привести интересные примеры поведения твердых тел под ударной нагрузкой. Например, при исследовании керамик повседневно проводятся ударные испытания керамических пластинок - свободно опертая квадратная пластинка подвергается удару заданной силы по центру верхней поверхности. Во многих случаях пластинка разрушается не в точке удара. Часто случается, что отваливаются четыре угла пластинки, потому что волны напряжений сталкиваются именно в углах.

Иногда случается, что, попав в броню, снаряд не пробивает ее, но от внутренней поверхности броневой плиты отлетает рваный кусок металла, осколок. Скорость и энергия этого осколка могут быть огромными, и разрушения, причиненные им внутри, например, танковой башни, оказываются такими же, как если бы снаряд действительно пробил броню.

Подобным же образом, когда снаряд или пуля попадает в бак с жидкостью, например в топливный бак самолета, выходное отверстие получается намного большим, и заделать его значительно труднее - ударные волны легко распространяются через жидкость и вырывают кусок в задней части бака. Голова человека конструктивно напоминает бак с жидкостью, и последствия попадания пули в нее, к сожалению, слишком хорошо известны. Менее известно, однако, что аналогичные события могут последовать за тупым ударом в лоб. При проектировании защитных касок заботятся о том, как погасить ударную волну и предохранить затылок при лобовом ударе. Этой цели и служит внутренняя лента в каске, которая на первый взгляд кажется необходимой лишь для вентиляции.

В технике вязкость материала определяется обычно путем ударных испытаний образца прямоугольного сечения размером 5-10 мм, часто снабженного стандартным надрезом. Образец закрепляют по концам, а затем разрушают тяжелым молотком в форме маятника. Измеряя разницу между высотой, с которой маятник падал на образец, и высотой, на которую он взлетел, разрушив его, определяют энергию, затраченную на разрушение. Строго говоря, это испытание почти ни о чем не говорит, но оно позволяет провести грубое сравнение различных материалов. Поэтому такие испытания очень популярны у инженеров.

(обратно)

Критерий Гриффитса и критическая длина трещины

Вернемся теперь к вопросу о распространении трещины в твердом теле. В данном случае для нас не имеет значения, статическая или динамическая нагрузка разрушает тело. Вообще говоря, если в данной точке достигнуто разрушающее напряжение, то разрушение произойдет независимо от того, каким путем оно достигалось. Правда, существуют некоторые исключения: отдельные вещества, вроде вара или конфеты ириски, чувствительны к скорости нагружения. Даже дети знают, что самую неподатливую ириску легко разломить, ударив по ней чем-нибудь. Иногда удар приводит к успеху там, где бесполезны медленные приемы (глава 8). Обычно же материалы, как правило, меньше чувствуют разницу между динамическим и статическим нагружением.

Конечно, идеально было бы иметь материал, в котором зарождение трещин совершенно исключено. К сожалению, на практике такого, кажется, не бывает. Мы видели в предыдущей главе, что даже самая гладкая поверхность стекла испещрена мельчайшими невидимыми трещинами; более того, если бы удалось получить бездефектную поверхность, она вскоре стала бы дефектной из-за соприкосновений с другими телами. Следовательно, практически все определяется легкостью, с которой трещины распространяются в нагруженном материале. Основы теории распространения трещин были заложены все тем же Гриффитсом.

Гриффитс указал два условия, необходимых для распространения трещины. Во-первых, рост трещины должен быть энергетически выгодным процессом, и, во-вторых, должен работать молекулярный механизм, с помощью которого может осуществиться преобразование энергии. Первое условие требует, чтобы на любой стадии распространения трещины количество запасенной в теле энергии уменьшалось - подобно тому, как уменьшается потенциальная энергия автомобиля, спускающегося с горы. С другой стороны, и при энергетической выгоде автомобиль может спускаться с горы лишь в том случае, если у него есть колеса и их не держат тормоза. Колеса в этом случае служат механизмом, с помощью которого автомобиль скатывается с горы, они обеспечивают преобразование энергии.

Как мы уже говорили, деформированное тело “начинено” энергией, которая предпочла бы высвободиться. Так, поднятый вверх камень имеет потенциальную энергию и стремится упасть. Если материал полностью разрушен, энергия деформации его, естественно, полностью освобождена. Рассмотрим, однако, что происходит на промежуточных этапах процесса разрушения. Когда в деформированном теле появляется трещина, она слегка раскрывается и оба ее края расходятся на некоторое расстояние. Это означает, что материал, непосредственно примыкающий к краям трещины, релаксирует, напряжения и упругие деформации в нем уменьшаются, и упругая энергия освобождается. Давайте проследим за трещиной, начавшейся на поверхности тела и идущей в глубь нагруженного материала (рис. 29). Понятно, что область срелаксировавшего материала будет приблизительно соответствовать двум заштрихованным треугольникам. Общая площадь этих треугольников будет примерно l2 (l - длина трещины). Следовательно, количество освобожденной энергии должно быть пропорционально квадрату длины трещины, или глубины ее проникновения в тело. Расчеты подтверждают эту грубую оценку. Иными словами, трещина глубиной 2 микрона высвобождает в 4 раза больше упругой энергии, чем трещина глубиной в микрон, и т.д.

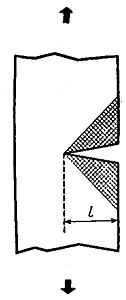
Рис. 29. Распространение трещины Гриффитса. С распространением трещины материал в заштрихованных областях разгружается, освобождая упругую энергию.

На другой чаше наших энергетических весов расположилась поверхностная энергия 2Gl, которая необходима для образования двух новых поверхностей. Очевидно, эта энергия пропорциональна первой степени длины (или глубины) трещины. Величины поверхностной энергии двухмикронной и одномикронной трещин отличаются лишь в 2 раза, в то время как величины освобожденной энергии деформации - в 4 раза. Последствия такого взвешивания достаточно ясны. Мелкая трещина для своего роста должна больше потреблять поверхностной энергии, чем производить свободной энергии вследствие релаксации напряжений. Эти условия невыгодны для роста трещины. Однако, если исходная трещина достаточно велика, картина изменяется на противоположную: с ростом размеров величина освобожденной энергии увеличивается быстрее, она ведь зависит от квадрата длины трещины. Получается, что, если длина трещины превышает некоторую “критическую длину Гриффитса”, трещина производит больше энергии, чем потребляет. Тогда она может с громадной скоростью рвануться вперед, и процесс этот будет подобен взрыву. Для каждой величины напряжения в данном материале существует своя критическая длина Гриффитса. Для теоретически максимальной величины напряжения (теоретической прочности) критическая длина бесконечно мала, для материала, свободного от напряжений, она бесконечно велика - иного мы и не должны были ожидать. К сожалению, для тех напряжений, с которыми нам приходится обычно иметь дело, критическая длина трещины, как правило, очень мала, порядка нескольких микрон, и, конечно, она уменьшается, когда мы пытаемся увеличить напряжение. В этом заключается одна из трудностей, связанных с получением более прочных материалов.

Итак, при обычных уровнях нагружений все трещины, за исключением самых мелких, имеют энергетический стимул к росту. Весь вопрос теперь в том, могут ли они расти. Иными словами, существует ли соответствующий механизм роста, то есть существует ли способ для реализации имеющейся энергетической выгоды, или преобразования одной формы энергии в другую? Гриффитсов баланс энергии, энергетическая выгода распространения трещины, длина которой превышает некоторую критическую величину, - явления совершенно общие для всех упругих тел. Но вот механизм преобразования энергии как раз и отличает вязкие материалы от хрупких.