Лит.: Радиоприемные устройства, под ред. В. И. Сифорова, М., 1974; Чистяков Н. И., Сидоров В. М., Радиоприемные устройства, М., 1974.

  В. М. Сидоров

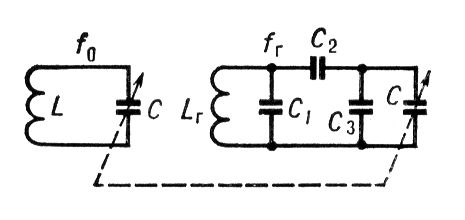
Принципиальная схема одного из контуров, содержащихся во входной цепи и в усилителе радиочастоты, и контура гетеродина: L и L_r — катушки индуктивности контуров; С — конденсаторы переменной ёмкости; C₁, С₂, С₃ — конденсаторы сопряжения; f_o и f_r — резонансные частоты контуров; пунктир означает, что ёмкости конденсаторов изменяются при помощи одной ручки настройки.

Сопряжение связей

Сопряже'ние свя'зей, один из важнейших видов внутримолекулярного взаимного влияния атомов и связей в органических соединениях; обусловлено взаимодействием электронных систем атомов (прежде всего валентных электронов, см. Валентность). Главный признак сопряжения — распределение по всей сопряжённой системе электронной плотности, создаваемой р- и p-электронами. Такими системами являются: чередующиеся простая и кратные связи — двойные или тройные; см. Простая связь, Кратные связи (p,p-сопряжение, как, например, в бутадиене, I; здесь и далее жирными штрихами, а также точками выделена сопряжённая система); кратная связь и атом со свободной электронной парой (р, p-сопряжение, например в винилхлориде, II); крестная связь и способная к сопряжению простая связь (s, p-сопряжение, например в хлормеркурацетальдегиде, III); две способные к сопряжению простые связи (s, s-сопряжение, например в этанолмеркурхлориде, IV). Такая классификация сопряжённых систем предложена в начале 50-х гг. 20 в. А. Н. Несмеяновым.

Общая особенность всех сопряжённых систем — «растекание» электронной плотности р- и p-электронов (см. Сигма- и пи-связи) по всей сопряжённой системе — определяет их физические и химические свойства. Так, простые связи приобретают некоторую «двоесвязность», выражающуюся, в частности, в уменьшении их длины. Например, в бутадиене длина центральной С — С-связи 1,46

 вместо обычной 1,54 . С. с. проявляется также, например, в УФ- и ИК-спектрах, дипольных моментах. Наиболее характерная химическая особенность сопряжённых систем — способность вступать в реакции не только с участием одной кратной связи, но и всей сопряжённой системы как единого целого. Примером может служить, например, присоединение к бутадиену хлористого водорода:

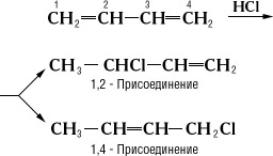
  Количество образующихся продуктов 1,2-и 1,4-присоединения зависит от природы сопряжённой системы, от реагента и условий реакции. Сопряжение снижает внутреннюю энергию молекул и, следовательно, делает их более устойчивыми: величина энергии сопряжения колеблется между несколькими единицами и десятками ккал/моль (например, для бутадиена 3,6 ккал/моль, для бензола 35 ккал/моль, 1 ккал/моль =4,19 кдж/моль).

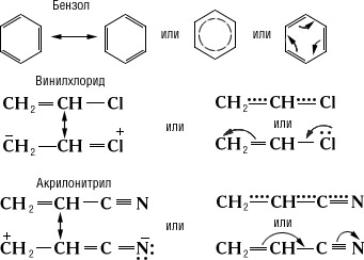
  Истинное распределение электронной плотности в сопряжённых системах нельзя выразить простейшими структурными формулами. Их строение более точно передаётся наборами предельных структур (см. Мезомерия, Резонанса теория), формулами с пунктирными («полуторными») связями или с изогнутыми стрелками, указывающими направление сдвига электронов, например:

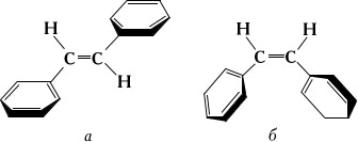
  Для проявления С. с. необходимо, чтобы участвующие в нём электронные системы находились в одной плоскости. Если структура молекулы не допускает этого, то говорят о пространственных препятствиях сопряжению. Так, у транс-стильбена (а), по данным УФ-спектров, обнаруживается более сильное сопряжение, чем у цис-стильбена (б), у которого бензольные ядра не могут разместиться в одной плоскости с двойной связью:

Сопряжённые гиперболы

Сопряжённые гипе'рболы, две гиперболы, которые в одной и той же системе прямоугольных координат при одних и тех же значениях а и b определяются уравнениями:

  и

  С. г. имеют общие асимптоты и общий основной прямоугольник (см. рис.).

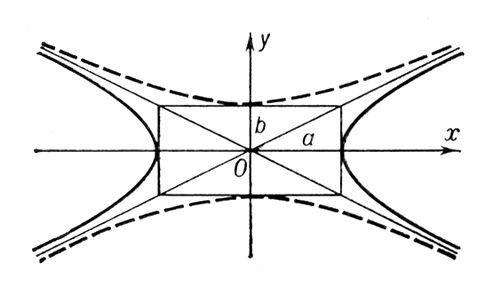
Рис. к ст. Сопряжённые гиперболы.

Сопряжённые диаметры

Сопряжённые диа'метры линии второго порядка, два диаметра, каждый из которых делит пополам хорды этой кривой, параллельные другому. С. д. играют важную роль в общей теории линий второго порядка. При параллельном проектировании эллипса в окружность его С. д. проектируются в пару взаимно перпендикулярных диаметров окружности.

Сопряжённые дифференциальные уравнения

Сопряжённые дифференциа'льные уравне'ния, понятие теории дифференциальных уравнений. Уравнением, сопряжённым с дифференциальным уравнением

 

, (1)

  называется уравнение

 

, (2)

  Соотношение сопряженности взаимно. Для С. д. у. имеет место тождество

 

,

  где y (у, z) — билинейная форма относительно у, z и их производных до (n - 1)-го порядка включительно. Знание k интегралов сопряжённого уравнения позволяет понизить на k единиц порядок данного уравнения. Если

  y₁, у₂,... у_n (3)

— фундаментальная система решений уравнения (1), то фундаментальная система решений уравнения (2) даётся формулами

 

 ,

  где D — определитель Вроньского (см. Вронскиан) системы (3). Если для уравнения (1) заданы краевые условия, то существуют сопряжённые с ними краевые условия для уравнения (2) такие, что уравнения (1) и (2) с соответствующими краевыми условиями определяют сопряжённые дифференциальные операторы (см. Сопряжённые операторы). Понятие сопряженности обобщается также на системы дифференциальных уравнений и на уравнения с частными производными.