Сопло

Сопло', специально спрофилированный закрытый канал, предназначенный для разгона жидкостей или газов до заданной скорости и придания потоку заданного направления. Служит также устройством для получения газовых и жидкостных струй. Поперечное сечение С. может быть прямоугольным (плоские С.), круглым (осесимметричные С.) или иметь произвольную форму (пространственное С.). ВС. происходит непрерывное увеличение скорости v жидкости или газа в направлении течения — от начального значения v_o во входном сечении С. до наибольшей скорости v = v_a на выходе. В силу закона сохранения энергии одновременно с ростом скорости v в С. происходит непрерывное падение давления и температуры от их начальных значений р_о, Т_о до наименьших значений р_а, Т_а в выходном сечении. Т. о., для реализации течения в С. необходим некоторый перепад давления, т. е. выполнение условия р_о > р_а. При увеличении Т_о скорость во всех сечениях С. возрастает в связи с ростом начальной потенциальной энергии. Пока скорость течения невелика, малы и соответствующие изменения давления и температуры в С., поэтому свойство сжимаемости (способность жидкости или газа изменять свой объём под действием перепада давления или изменения температуры) ещё не проявляется, и изменением плотности среды r в направлении течения можно пренебречь, считая её постоянной. В этих условиях для непрерывного увеличения скорости С. должно иметь сужающуюся форму, т.к. в силу уравнения неразрывности rvF = const площадь F поперечного сечения С. должна уменьшаться обратно пропорционально росту скорости. Однако при дальнейшем увеличении v начинает проявляться сжимаемость среды, плотность её уменьшается в направлении течения. Поэтому постоянство произведения трёх множителей rvF в этих новых условиях зависит от темпа падения r с ростом v. При v < a, где а — местная скорость распространения звука в движущейся среде, темп падения плотности газа отстаёт от темпа роста скорости, поэтому для обеспечения разгона, т. е. увеличения v, F нужно уменьшать (рис. 1), несмотря на падение плотности (дозвуковое С.). Но при разгоне до скоростей v>a падение плотности происходит быстрее, чем рост скорости, поэтому в сверхзвуковой части необходимо увеличивать площадь F (сверхзвуковое С.). Т. о., сверхзвуковое С., называемое также соплом Лаваля, имеет вначале сужающуюся, а затем расширяющуюся форму (рис. 2). Изменение скорости вдоль С. определяется законом изменения площади его поперечного сечения F по длине С.

  Давление в выходном сечении дозвукового С. всегда равно давлению р_с в окружающей среде, куда происходит истечение из С. (р_а = р_с), т.к. любые отклонения в величине давления представляют собой возмущения, которые распространяются внутрь С. со скоростью, равной скорости звука, и вызывают перестройку потока, ведущую к выравниванию давлений в выходном сечении С. При возрастании р_о и неизменном р_с скорость v_a в выходном сечении дозвукового С. сначала увеличивается, а после того как р_о достигнет некоторой определённой величины, v_a становится постоянной и при дальнейшем увеличении р_о не изменяется. Такое явление называется кризисом течения в С. После наступления кризиса средняя скорость истечения из дозвукового С. равна местной скорости звука (v_a = а) и называется критической скоростью истечения. Дозвуковое С. превращается в звуковое С. Все параметры газа в выходном сечении С. также называются в этом случае критическими. Для дозвуковых С. с плавным контуром критическое отношение давлений при истечении воздуха и др. двухатомных газов (р_о/р_с) _кр » 1,9.

  В сверхзвуковом С. критическим называют его наиболее узкое сечение. Относительная скорость v_a/a в выходном сечении сверхзвукового С. зависит только от отношения площади выходного сечения F_a к площади его критического сечения F_kp и в широких пределах не зависит от изменений давления р_о перед С. Поэтому, изменяя с помощью механического устройства площадь критического сечения F_kp при неизменной площади F_a, можно изменять v_a/a. На этом принципе основаны используемые в технике регулируемые С. с переменной скоростью газа в выходном сечении. Давление в выходном сечении сверхзвукового С. может быть равно давлению в окружающей среде (р_а = р_с), такой режим течения называется расчётным, в противном случае — нерасчётным. В отличие от дозвукового С., возмущения давления при p_a ¹ р_с, распространяющиеся со скоростью звука, относятся сверхзвуковым потоком и не проникают внутрь сверхзвукового С., поэтому давление р_а не уравнивается с р_с. Нерасчётные режимы характеризуются образованием волн разрежения в случае р_а > р_с или ударных волн в случае р_а < р_с Когда поток проходит через систему таких волн вне С., давление становится равным р_с. При большом избытке давления в атмосфере над давлением в выходном сечении С. ударные волны могут перемещаться внутрь С., и тогда нарушается непрерывное увеличение скорости в сверхзвуковой части С. Сильное падение давления и температуры газа в сверх звуковом С. может приводить, в зависимости от состава текущей среды, к различным физико-химическим процессам (химические реакции, фазовые превращения, неравновесные термодинамические переходы), которые необходимо учитывать при расчёте течения газа в С.

  С. широко используются в технике (в паровых и газовых турбинах, в ракетных и воздушно-реактивных двигателях, в газодинамических лазерах, в магнитно-газодинамических установках, в аэродинамических трубах и на газодинамических стендах, при создании молекулярных пучков, в химической технологии, в струйных аппаратах, в расходомерах, в дутьевых процессах и многих др.). В зависимости от технического назначения С. возникают специфические задачи расчёта С.: например, в С. аэродинамических труб необходимо обеспечить создание равномерного и параллельного потока газа в выходном сечении, требования к С. ракетных двигателей заключаются в получении наибольшего импульса газового потока в выходном сечении С. при его заданных габаритных размерах. Эти и др. технические задачи привели к бурному развитию теории С., учитывающей наличие в газовом потоке жидких и твёрдых частиц, неравновесных химических реакций, переноса лучистой энергии и др., что потребовало широкого применения ЭВМ для решения указанных задач, а также для разработки сложных экспериментальных методов исследования С.

  Лит.: Абрамович Г. Н., Прикладная газовая динамика, 3 изд., М., 1969: Стернин Л. Е., Основы газодинамики двухфазных течений в соплах, М., 1974.

  С. Л. Вишневецкий.

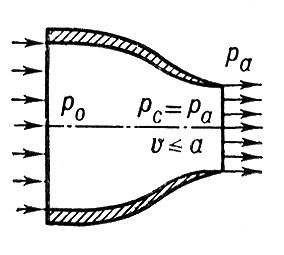
Рис. 1. Схема дозвукового сопла.

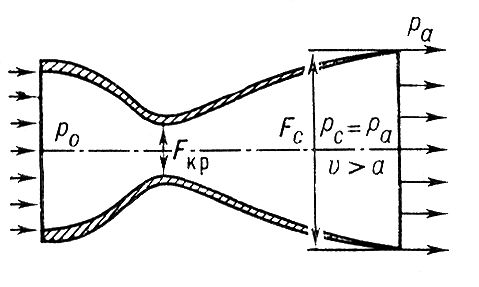
Рис. 2. Схема сверхзвукового сопла (сопла Лаваля).