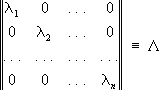
Каждую матрицу А с различными С. з. можно представить в виде С–1LС. Если А — самосопряжённая матрица, то её С. з. действительны, собственные векторы ортогональны, а матрицу С можно выбрать унитарной (см. Унитарная матрица). Модуль каждого С. з. унитарной матрицы равен 1. Сумма С. з. матрицы равна сумме её диагональных элементов, т. е. следу её матрицы. Знание С. з. матрицы играет важную роль в исследовании сходимости некоторых приближённых методов решения систем линейных уравнений. См. также Собственные функции.
Собственные имена
Со'бственные имена', слова или словосочетания, называющие, в отличие от нарицательных имен, единичное или собирательное лицо или объект в его цельности и единственности, индивидуализирующие его, однозначные для него вне зависимости от контекста. Общим отличительным признаком С. и. (если пренебречь некоторыми семантическими особенностями отдельных групп) служит денотативный характер их значения (см. Знак языковой). Центром класса, наиболее «подлинными» С. и. являются имена личные (см. Ономастика); все С. и. генетически — нарицательные имена, чёткой границы между ними нет (ср. этнонимы, товарные знаки); С. и. с ясной и затемнённой внутренней формой употребляются одинаково (Новгород, Москва). В системе отношений с др. единицами словаря С. и. занимают изолированное место. Языковая информация их меньше, а культурная — значительно больше, чем нарицательных. В разных науках, изучающих С. и. (лингвистика, логика, философия, мифология и др.), объём класса и его определение не совпадают.
Для мифолого-символического сознания, сводящего язык к набору имён и считающего С. и. словами, наиболее точно выполняющими функцию именования, они стоят в центре онтологии языка. В ряде античных и средневековых теорий они признавались знаками, связанными с сущностью именуемого, символически причастными его глубинной тайне. Имманентное (не фонетическое или графическое) имя, истолкованное по аналогии с идеями Платона, рассматривалось как корень индивидуального бытия. Это учение было возрождено и развито в 20 в. (П. А. Флоренский, С. Н. Булгаков, М. Хайдеггер). Крайним выражением его является отождествление имени с именуемым или приписывание мистических свойств имязвучию или имяначертанию, представление о конденсации в имени мощи именуемого, из чего исходят словесная магия и табу. Ему противостоят рационалистические воззрения, идущие от Демокрита, обосновавшего произвольность (условность) природы всякого имени. К. Маркс считал, что название какой-либо вещи не имеет ничего общего с её природой. Лингвисты и логики, развивающие это направление, считают С. и. немотивированными знаками, одним из способов обозначения точек пространственно-временной действительности; они могут быть заменены другими знаками (переименование), номерами (как улицы в Нью-Йорке), алгебраическими символами. Выбор С. и. и объём их класса определяют экстрасемиотические причины (например, списки канонических личных имён в христианстве или мусульманстве); связь между именем и именуемым существует не в реальной действительности, а лишь в сознании именующих.
Лит.: Волошинов В. Н., Марксизм и философия языка, Л., [1929]; Булгаков С. Н., Философия имени, Париж, [1953]; Суперанская А. В., Общая теория имени собственного, М., 1973; Никонов В. А., Имя и общество, М., 1974.
Ю. М. Эдельштейн.
Собственные колебания
Со'бственные колеба'ния, свободные колебания, колебания в механической, электрической или какой-либо другой физической системе, совершающиеся при отсутствии внешнего воздействия за счёт первоначально накопленной энергии (вследствие наличия начального смещения или начальной скорости). Характер С. к. определяется главным образом собственными параметрами системы (массой, индуктивностью, ёмкостью, упругостью). В реальных системах вследствие рассеяния энергии С. к. всегда затухающие, а при больших потерях они становятся апериодическими. Подробнее см. в статье Колебания.
Собственные нужды электростанции
Со'бственные ну'жды электроста'нции, комплекс вспомогательного электрического оборудования электростанции, обеспечивающего бесперебойную работу её основных агрегатов (паровых котлов, турбогенераторов, ядерных реакторов или гидротурбин). В состав С. н. э. входят: силовая и осветительная электросети станции, аккумуляторные установки, аварийные источники электропитания, электродвигатели всех механизмов — насосов (водяных, нефтяных, масляных и т.д.), вентиляторов, а на наиболее распространённых тепловых электростанциях — также механизмов разгрузки железнодорожных вагонов, подачи топлива, угледробления и пылеприготовления.
Электроприёмники С. н. э. подразделяют на группы в соответствии с требованиями бесперебойной работы. К группе наиболее ответственных (HO) относят электроприёмники, выход из строя которых приводит к нарушению нормального режима работы станции или к аварии. На ТЭС это — электродвигатели питательных насосов паровых котлов, на АЭС — системы управления и защиты реактора, механизмы расхолаживания реактора, на ГЭС — механизмы, обеспечивающие циркуляцию масла и воды в системах смазки и охлаждения, механизмы закрытия дроссельных затворов напорных трубопроводов. Организация работы HO электроприёмников предусматривает их надёжное резервирование, обеспечивающее высокую надёжность устройств С. н. э. Затраты электроэнергии на работу С. н. э. составляют (в % от общего кол-ва электроэнергии, вырабатываемой станцией) от 0,2 на ГЭС большой мощности до 12 на АЭС с. газовым теплоносителем.
Лит.: Баптиданов Л. Н., Тарасов В. И., Электрооборудование электрических станций и подстанций, 3 изд., т. 1–2, М. — Л., 1959—60; Электротехнический справочник, 4 изд., т. 2, кн. 1, М., 1972.
Б. А. Князевский.
Собственные функции
Со'бственные фу'нкции, понятие математического анализа. При решении многих задач математической физики (в теории колебаний, теплопроводности и т.д.) возникает необходимость в нахождении не равных тождественно нулю решений однородных линейных дифференциальных уравнений L (y) = lу, удовлетворяющих тем или иным краевым условиям. Такие решения называют С. ф. задачи, а соответствующие значения l — собственными значениями. Если дифференциальное уравнение с соответствующими краевыми условиями самосопряжённое (см. Самосопряжённое дифференциальное уравнение), то его собственные значения действительны, а С. ф., соответствующие различным собственным значениям, ортогональны. Если дифференциальное уравнение рассматривается на конечном отрезке и его коэффициенты не имеют на этом отрезке особенностей, то множество С. ф. счётно (задача имеет дискретный спектр); знание С. ф. и соответствующих собственных значений позволяет тогда при некоторых условиях получить решение задачи в виде ряда по С. ф. (см. Фурье метод). Если же уравнение рассматривается на бесконечном промежутке или его коэффициенты имеют особенности (например, если коэффициент при старшей производной обращается в нуль), может существовать континуум С. ф., и вместо разложения в ряд получается разложение в интеграл по С. ф., аналогичное представлению в виде Фурье интеграла. В этом случае говорят, что задача имеет непрерывный спектр. Многие специальные функции (ортогональные многочлены и др.) служат С. ф. некоторых уравнений.