Равновесные межъядерные расстояния r ₀ и энергии диссоциации D (при 25°С) некоторых двухатомных молекул

Молекула	r0,	кдж/моль ккал/моль	Молекула	r	D,Кдж/моль ккал/моль
2	0,74	426,5 (104,18)	2	2,14	192,7 (46)
2	2,67	104,7 (25)	2	2,67	147,1 (35,1)
2	1,09	94,3 (22,5)	LiH	1,59	243 (58)
2	1,21	495,7 (118,3)	NaH	1,89	196,9 (47)
2	1,48	155 (37)	HhF	0,92	565,6 (135)
2	3,08	78,5 (17,3)	HCl	1,27	431,6 (103)
2	1,99	242,6 (57,9)	HI	1,60	264 (63)

  Строение молекул. Геометрическая структура М. определяется равновесным расположением атомных ядер. Энергия взаимодействия атомов зависит от расстояния между ядрами. На очень больших расстояниях эта энергия равна нулю; если при сближении атомов образуется химическая связь, то атомы сильно притягиваются друг к другу (слабое притяжение наблюдается и без образования химической связи); при дальнейшем сближении атомов действуют электростатические силы отталкивания атомных ядер; препятствием к сильному сближению атомов является также невозможность совмещения их внутренних электронных оболочек. На рис. 1 показана зависимость потенциальной энергии двухатомной М. от межъядерного расстояния r . Эта энергия минимальна при равновесном расстоянии r , стремится к нулю при r ® ¥ и возрастает до ¥ при r ® 0. Разность энергий при r = r и r ® ¥ характеризует энергию связи, энергию диссоциации D . Равновесные расстояния r в двухатомных и многоатомных М. и, следовательно, расположение атомных ядер в М. определяются методами спектроскопии, рентгеновского структурного анализа и электронографии , а также нейтронографии , позволяющими получить сведения и о распределении электронов (электронной плотности) в М. Рентгенографическое изучение молекулярных кристаллов даёт возможность установить геометрическое строение очень сложных М., вплоть до М. белков. Косвенную, но весьма детальную информацию о строении сложных М. получают различными спектроскопическими методами, в особенности с помощью спектров ядерного магнитного резонанса (ЯМР). Геометрия простых М., содержащих малое число атомов, также эффективно исследуется методами спектроскопии. Расстояния (в Ǻ) между 2 данными валентно связанными атомами приблизительно постоянны в М. различных соединений, они уменьшаются с увеличением кратности связи:

C—C…………….	1,54	C—F……………..	1,39
C=C……………...	1,34	C—Cl…………….	1,77
C- - -C (в бензоле)...	1,39	C—Br…………….	1,92
CºC……………...	1,2	C—I………………	2,1
C—H……………..	1,09	C—S……………..	1,82
C—O……………..	1,42	O—H…………….	0,96
C=O……………...	1,21	N—H……………..	1,01
C—N……………..	1,46	S—H……………..	1,35

Можно приписать каждому атому в данном валентном состоянии в М определённый атомный, или ковалентный, радиус (в случае ионной связи — ионный радиус, см. Атомные радиусы , Ионные радиусы ), характеризующий размеры электронной оболочки атома (иона), образующего химическую связь в М. Представление о приблизительном постоянстве этих радиусов оказывается полезным при оценке межатомных расстояний и, следовательно, при расшифровке структуры М. Длина связи представляет собой сумму соответствующих атомных радиусов.

  Размер М. как целого, т. с. размер её электронной оболочки, есть величина до некоторой степени условная — имеется отличная от нуля, хотя и весьма малая, вероятность найти электроны М. и на большом расстоянии от её атомных ядер. Практически размеры М. определяются равновесным расстоянием, на которое они могут быть сближены при плотной упаковке М. в молекулярном кристалле и в жидкости. На больших расстояниях М. притягиваются одна к другой, на меньших — отталкиваются. Размеры М. поэтому можно найти с помощью рентгеноструктурного анализа молекулярных кристаллов, порядок величины этих размеров может быть определён из коэффициентов диффузии, теплопроводности и вязкости газов и из плотности вещества в конденсированном состоянии. Расстояние, на которое могут сблизиться валентно не связанные атомы, принадлежащие одной и той же М. или различным М., может быть охарактеризовано средними значениями т. н. ван-дер-ваальсовых радиусов (в Ǻ):

H……...	1,0-1,2	S………	1,9
C……...	1,75-2,0	Se……..	1,0
N……...	1,5	Te……..	2,2
P………	1,9	F………	1,4
As……..	2,0	Cl……...	1,8
Sb……..	2,2	Br……...	2,0
O………	1,4	I……….	2,2

  Ван-дер-ваальсовы радиусы существенно превышают ковалентные. Зная величины ван-дер-ваальсовых, ковалентных, а также ионных радиусов, можно построить наглядные модели М., отражающие форму и размеры их электронных оболочек (рис. 2 ).

  Ковалентные химические связи в М. расположены под определёнными углами, зависящими от состояния гибридизации атомных орбиталей (см. Валентность ). Так, для М. насыщенных органических соединений характерно тетраэдрическое расположение связей, образуемых атомом углерода; для М. с двойной связью (С=С) — плоское расположение связей атомов углерода; в М. соединений с тройной связью (СºС) — линейное расположение связей:

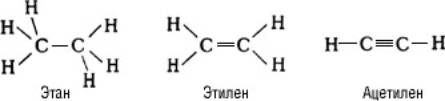
  Таким образом, многоатомная М. обладает определённой конфигурацией в пространстве, т. е. определённой геометрией расположения связей, которая не может быть изменена без их разрыва. М. характеризуется той или иной симметрией расположения атомов. Если М. не имеет плоскости и центра симметрии, то она может существовать в двух конфигурациях, представляющих зеркальные отражения одна другой (зеркальные антиподы, или стереоизомеры, см. Изомерия ). Все важнейшие биологически функциональные вещества в живой природе фигурируют в форме одного определённого стерсоизомера.

  М., содержащие единичные связи, или сигма-связи, могут существовать в различных конформациях , возникающих при поворотах атомных групп вокруг единичных связей. Важные особенности макромолекул синтетических и биологических полимеров определяются именно их конформационными свойствами.

  Взаимодействие атомов в молекуле. Природа химических связей в М. оставалась загадочной вплоть до создания квантовой механики — классическая физика не могла объяснить насыщаемость и направленность валентных связей. Основы теории химической связи были созданы В. Гейтлером и немецким учёным Ф. Лондоном в 1927 на примере простейшей молекулы Н₂ . В дальнейшем теория и методы расчёта были значительно усовершенствованы, в частности на основе широкого применения молекулярных орбиталей метода , и квантовая химия позволяет вычислять межатомные расстояния, энергии М., энергии химических связей и распределение электронной плотности для сложных М.; при этом расчётные данные хорошо согласуются с экспериментальными.