На рис. 1 числа Фибоначчи выражают длины сторон спиральной последовательности квадратов на клетчатой бумаге. Из этого рисунка нетрудно получить такое равенство: u₁² + u₂² + u₃² + ... + u_n² = u_n u_n+1 (для любого n). Это и другие любопытные соотношения между числами Фибоначчи, такие, как

u₁ + u₂ + ... + u_n = u_n+2 - 1;

u²_n - u_n-1u_n+1 = u_n+2u_n-1 - u_nu_n-1 = (-1)ⁿ;

u_m+k = u_k-1u_m + u_ku_m+1,

можно доказать методом математической индукции.

Рис. 1

Много интересного в арифметике чисел Фибоначчи. Каждое третье число Фибоначчи четно, каждое четвертое делится на три, каждое пятнадцатое оканчивается нулем, и вообще для каждого d числа Фибоначчи, делящиеся на d, встречаются периодически. Два соседних числа Фибоначчи взаимно просты; u_m делится на u_n тогда и только тогда, когда m делится на n.

При детальном исследовании свойств делимости чисел Фибоначчи выясняется особая роль числа 5, например: если простое число p имеет вид 5t±2, то u_p+1 делится на p, а если p имеет вид 5t±1, то u_p-1 делится на p.

Число 5 участвует и в приведенной ниже формуле Бине (французский ученый Ж. Вине, 1786-1856), выражающей u_n как функцию от номера n:

.

Из этой формулы следует, что u_n растет примерно как геометрическая прогрессия со знаменателем

,

точнее, u_n равно ближайшему целому числу к τⁿ/√5.

Формулу Бине можно доказать по индукции или с помощью производящей функции для последовательности Фибоначчи:

.

Выражение для n-го члена в виде суммы нескольких геометрических прогрессий, аналогичное формуле Бине, можно написать и для других последовательностей, определяемых соотношением x_n+r = a₀x_n + a₁x_n+1 + ... + a_r-1x_n+r-1. Знаменатели этих прогрессий находятся как корни так называемого характеристического многочлена p(λ) = λ^r - a_r-1λ^r-1 - ... - a₁λ - a₀. Например, для последовательности Фибоначчи характеристический многочлен равен λ² - λ - 1. В общем случае надо использовать не только вещественные, но и комплексные корни многочлена (а если к тому же у него какой-то корень λ имеет кратность k > 1, то кроме геометрической прогрессии c λⁿ в сумму могут входить еще последовательности c₁nλⁿ, c₂n²λⁿ,...,c_k-1n^k-1λⁿ - тогда общее число членов в сумме будет всегда равно r).

Пусть через один такт времени красная клетка превращается в зеленую, а та в свою очередь через один такт делится на две - красную и зеленую. Тогда число клеток каждого поколения можно выразить числом Фибоначчи

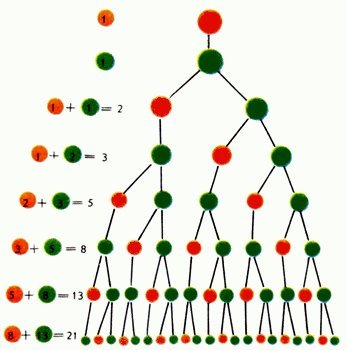
Уже в нашем веке были найдены новые свойства и применения чисел Фибоначчи. Среди них - самый быстрый способ отыскания экстремума для функции y=f(x) с двумя промежутками монотонности [a, x^*] и [x^*, b] (т.е. с одним экстремумом): оказывается, в наилучшем плане поиска точки экстремума x^*, состоящего из n шагов, участвуют числа Фибоначчи u₁,u₂,...,u_n+2.

ФИГУРНЫЕ ЧИСЛА

Про числа 25, 49, 100 говорят, что они являются квадратами. А почему? Потому что они получаются, если возвести числа 5, 7 и 10 в квадрат. Но имеет ли это название какое-нибудь отношение к геометрической фигуре - квадрату? Посмотрим на рис. 1. Солдаты стоят правильными рядами, образуя квадраты. Число солдат внутри такого квадрата легко подсчитать - нужно умножить их число вдоль горизонтальной стороны на число солдат вдоль вертикальной стороны (заметим, что эти числа равны), и получится общее количество солдат внутри квадрата.

Рис. 1

В древности вычислители часто считали с помощью камешков и, естественно, отмечали случаи, когда камешки можно было сложить в виде правильной фигуры. Кроме квадратных чисел были известны треугольные числа, которые получаются так, как это показано на рис. 2 в верхней его части. Нетрудно заметить, что n-е квадратное число равно n², а n-е треугольное число равно сумме всех целых чисел от 1 до n, т.е. n(n+1)/2 (см. Арифметическая прогрессия).

Рис. 2

Пятиугольные числа изображены на рис. 2. Чтобы сосчитать n-е пятиугольное число, его нужно разбить на три треугольных, после чего останется еще n точек, как показано на рисунке. В результате получаем, что n-е пятиугольное число равно

.

Подобным образом можно образовывать любые многоугольные числа. Формула для n-го k-угольного числа такова:

.

При k=3 мы получаем треугольные числа, при k = 4 - квадратные и т.д.

Аналогично можно представить число в виде прямоугольника. Для числа 12 это можно сделать многими способами (рис. 2), а для числа 13 - лишь расположив все предметы в одну линию. Такое число древние не считали прямоугольным. Таким образом, прямоугольными числами являются все составные числа, а непрямоугольными - простые числа.

К фигурным числам также относятся пирамидальные числа, которые получаются, если шарики складывать пирамидой, как раньше складывали ядра около пушки. Нетрудно заметить, что n-е пирамидальное число равно сумме всех треугольных чисел - от первого до n-го. Формула для вычисления n-го пирамидального числа имеет вид

n_n=n(n+1)(n+2)/6.

ФОРМУЛА

Формула комбинация математических знаков и букв, выражающая какое-либо предложение.

Например, формула синуса тройного угла (см. Угол), выражающая его через синус простого угла:

sin 3α = 3 sin α - 4 sin³α.

Известно много формул, связывающих между собой элементы треугольника (a, b, c - длины сторон, r и R - радиусы вписанной и описанной окружностей). Вот одна из них:

1/ab+ 1/bc + 1/ca = 1/2Rr.

Как правило, термин «формула» употребляют по отношению к комбинациям знаков и букв, которые:

состоят из двух частей, соединенных знаком равенства;

выражают истинное при определенных условиях утверждение;

позволяют выразить некоторую величину через другие.

Особое значение термин «формула» приобретает в математической логике, где он применяется по отношению к выражениям формального языка, построенным по определенным правилам.

ФУНКЦИЯ

Функция - это одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами.