+ х (ab + ас + bc) — abc = 0,

откуда следует, что коэффициенты уравнения третьей степени связаны с корнями следующим образом:

А = — (а + b + с); В = ab + ас + bc; С = — abc.

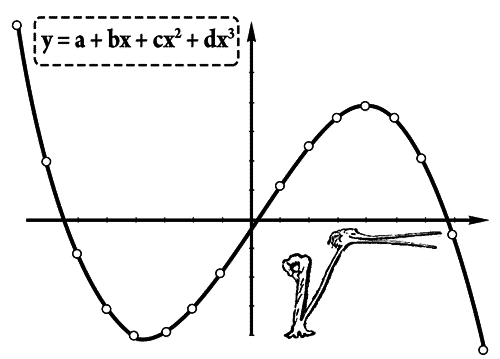
Три вещественных корня.

— 331 —

Рассмотрим теперь, что обозначает геометрически утверждение о трех корнях. Если мы напишем

у = х³ + Ах² + Вх + С,

то будем иметь дело с кривой, которая сперва поднимается вверх, доходит до некоторого максимума, потом опускается, доходит до некоторого минимума, а затем снова начинает подниматься. Разумеется, все это может идти и обратным порядком (то есть сперва будет минимум, а потом максимум), в зависимости от знака перед х³ (все эти кривые называются кубическими параболами, параболами третьего порядка). Но если кривая имеет такую форму, то ясно, что она либо пересекает ось иксов трижды, и тогда все три корня кубического уравнения вещественны, либо пересекает ее только однажды, и тогда у него есть лишь один вещественный корень и два других — комплексные. Все рассуждения чрезвычайно упрощаются. Что же касается тех преимуществ, которые дает алгебра, то легко рассудить, что гораздо проще написать

х² = аb.

чем выполнить построением и записать такое утверждение:

«Квадрат, построенный на отрезке, длина которого равняется х, равновелик прямоугольнику, одна сторона которого равна а, а другая равна b». Тут надо вот еще что иметь в виду. Геометрия древних, как отчасти и геометрия вообще, отличается тем, что там нет общих способов и чуть ли не каждая задача решается по-своему. Греки проявили в таких решениях просто гениальное остроумие, но им не хватало того, что ныне мы называем общностью. Они сделали все, что было возможно при отсутствии общих методов, а далее вынуждены были остановиться. Труды Архимеда были замечательны еще тем, что он в связи с развитием в его время естественных наук (особенно астрономии) обратил внимание на измерение и вычисление, но и у него общие методы не выработаны, а только намечены. Труды средневековых алгебраистов и математиков эпохи Возрождения много сделали для объединения и систематизации математической работы. Декарту же вместе с Ферма посчастливилось, соединив воедино геометрию с алгеброй, дать

— 332 —

математикам в руки способ (метод) для рассмотрения и решения труднейших задач, где геометрия и алгебра помогают друг другу. Именно метод координат и аналитическая геометрия помогли решить одну замысловатую задачу, над которой математики бились с давних пор.

— А какая это задача? — спросил Илюша.

— Это была знаменитая задача о проведении касательной. А построить касательную к окружности нетрудно.

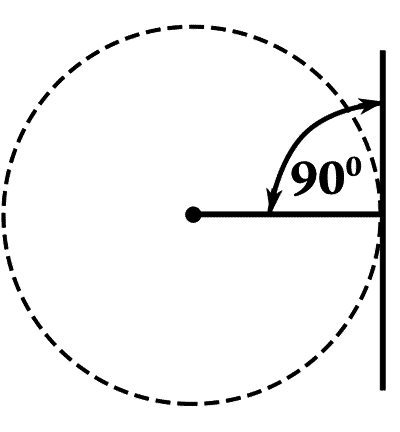
Касательная к окружности перпендикулярна к радиусу.

— Конечно, — отвечал Илюша, — потому что эта касательная перпендикулярна к радиусу.

— Правильно. Ну, а как ты проведешь касательную к любой другой кривой? Ну, например, к той же параболе? Или к кривой обратных величин, то есть к гиперболе? У параболы, например, нет радиуса.

Илюша задумался.

— А что, если сделать так. Например, надо провести касательную к данной точке параболы. Я начерчу окружность, очень похожую на параболу на этом ее кусочке, вроде тех кругов, которыми Коникос мерил кривизну. А к окружности касательную провести ничего не стоит.

— Представь себе, что и мысль Декарта шла примерно таким же образом. Нужно тебе сказать, что и до Декарта мате—

Кривая сначала поднимается (ордината ее растет), и касательная образует с положительным направлением оси абсцисс острый угол α

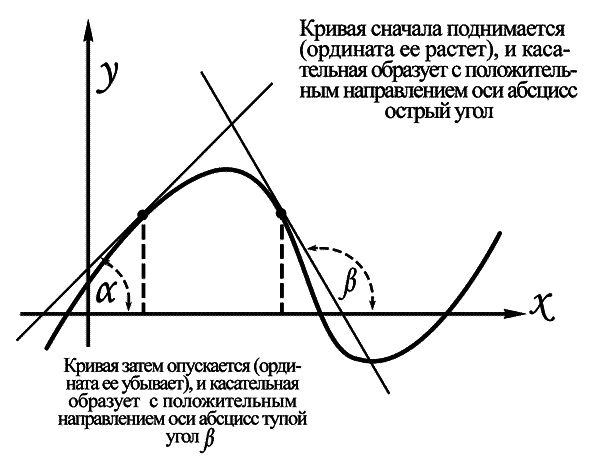
Кривая затем опускаетсся (ордината ее убывает), и касательная образует с полжительным направлением оси абсцисс тупой угол β

— 333 —

матики проводили касательные к различным кривым, но только у них не было общего правила для этого. Перпендикуляр к касательной, как мы уже говорили в Схолии Четырнадцатой, называется нормалью кривой в данной точке. Так вот Декарт и нашел общее правило для построения нормалей. А отсюда уже не так-то трудно перейти и к самим касательным.

— Это интересно, — сказал Илюша. — Но разве это так важно — уметь провести касательную к любой кривой?

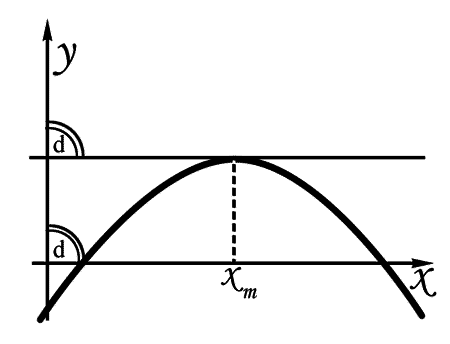
В точке, соответствующей х, кривая достигает максимума и касательная становится параллельной оси абсцисс.

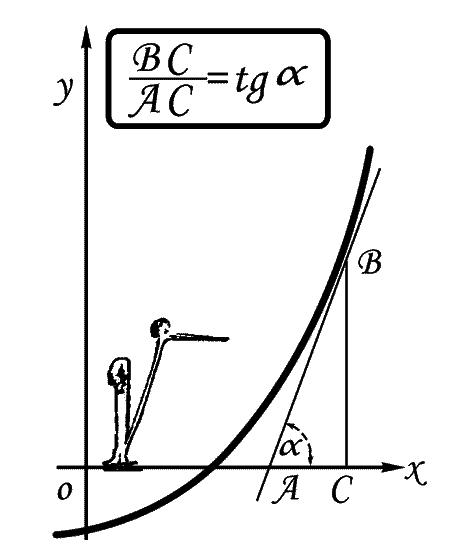
Чем скорее растет ордината кривой, тем больше угол α и его тангенс.

— Сперва казалось, что это просто одна из трудных геометрических задач. Однако Декарт во второй книге своей «Геометрии» писал:

«Я готов даже сказать, что эта задача является самой полезной и обладает наибольшей общностью не только из тех задач, которые мне известны, но даже изо всех тех, которые мне хотелось когда бы то ни было узнать». Кеплер в своем сочинении о стереометрии винных бочек отметил некоторые особые свойства кривых, которые тесно связаны с касательными их. Мы вот сейчас говорили о том, что у кубической параболы есть максимум и минимум. Если ты внимательно посмотришь на график этой кривой, то заметишь, что ордината этой параболы сперва растет очень скоро, а потом все медленнее и медленнее. В точке максимума ее рост прекращается, а потом начинает падать.

— Так, — сказал Илюша. — А с минимумом наоборот: падает, падает, потом останавливается в точке минимума, а потом снова начинает расти.

— Молодец! — похвалил Радикс. — Кое-как соображаешь.

— 334 —

— Кое-как могу, когда не очень трудно, — отвечал мальчик, — да и то потому, что ты помогаешь.

— Отчего же и не помочь человеку, если он старается разобраться в том, что ему объясняют! Ну, а теперь пораскинь-ка мозгами и ответь мне на такой вопрос: что будет делать касательная к этой кривой, если я буду строить ее для различных точек кубической параболы и на чертеже брать эти точки одну за другой слева направо до максимума и после него?

Как будет наклонена касательная по отношению к положительному направлению оси абсцисс?

— По-моему, — сказал Илюша, — она до максимума будет наклонена в одну сторону, а после максимума — в другую.

— Это верно, — сказал Радикс, — а поточнее? Какой угол будет образовывать касательная с положительным направлением оси абсцисс, если мы продолжим касательную до пересечения с этой осью- до максимума и после него?

— До максимума, — ответил Илюша, — кривая поднимается, значит, верхняя часть касательной будет образовывать с положительным направлением оси абсцисс острый угол, а после максимума кривая опускается, зна—

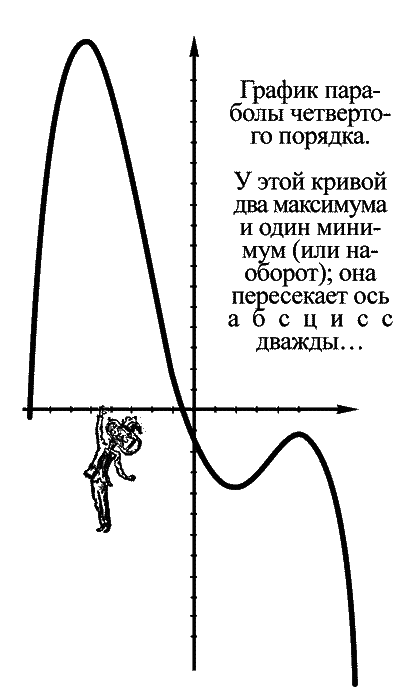
График параболы четвертого порядка.

У этой кривой два максимума и один минимум (или наоборот); она пересекает ось абсцисс дважды…

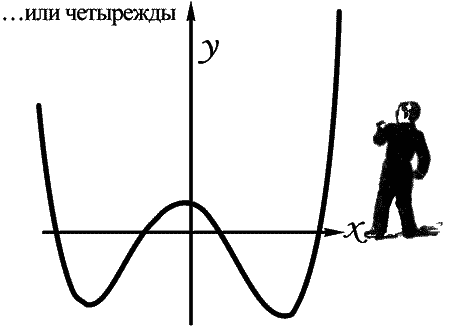
… или четырежды.

— 335 —

чит, верхняя часть касательной образует с положительным направлением оси абсцисс тупой угол.

— Круглая пятерочка! — воскликнул Радикс. — Отвечай, юноша, что же будет с касательной в точке максимума?