— Не на «что-то», а на множители — 3, 2, 6, 4, 5, 8, 9, 10,11, 23 и 89. И всё!
— Что же тут трудного? — спросил Илюша.
— Трудного ничего нет. Но самое ужасное заключается в том, что на что ни множь это проклятое число, получается все то же самое. В нем есть какой-то центр. Какой? Не могу понять. И вот вокруг него-то это заколдованное число и вертится, как колесо!
Тут Уникурсал Уникурсалыч на минутку выскочил и быстро прикатил здоровенное колесо, на котором было написано злополучное число.
Против начальной единицы командор поставил на стене мелом крестик.
— О ты, очаровательный отрок, постигший таинства умножения! Ну-ка, давай умножать.
— 149 —
Илюша начал множить 142 857 на три. Получилось 428 571.
Командор повернул влево свое колесо на одну цифру. Действительно, против крестика теперь стояла четверка, а все остальное шло тем же порядком.
Илюша посмотрел недоуменно на колесо и начал множить на два. Вышло 285 714. Командор передвинул колесо еще на одну цифру. И опять дальше все пошло в том же порядке.
Илюша помножил на шесть. Вышло 857142. Колесо подвинулось еще на одну цифру. Помножили на четыре. Получилось 571428. Колесо снова повернулось на одну цифру. Помножили на пять. Вышло 714 285.
— Видишь! — вскричал, вытаращив глаза, Уникурсал Уникурсалыч. — Разве это число? Ты множишь, стараешься, обливаешься потом, а оно вертится да вертится!
— Ну, дальше ему уже вертеться некуда, — заметил Илюша.
— Как бы не так! Ты посмотри, что дальше будет.
Илюша умножил на восемь. Вышло 1142 856.
— Ну, — сказал магистр, — возьми эту лишнюю единицу, которая торчит спереди, и прибавь к последней цифре.
Илюша прибавил, и вышло опять 142857.
— Теперь на девять, — потребовал командор.
Умножили на девять. Получилось 1285713. А когда первую единицу прибавили к последней цифре, вышло 285714.
— 150 —
— Та же самая история, что с двойкой! — сокрушенно сказал командор.
Умножили на десять. Вышло 1428570. А когда прибавили сзади первую единицу, то снова получилось 428571, как было с тройкой. Умножили на одиннадцать. Получилось 1571427. Опять прибавили переднюю единицу к последней цифре, получилось 571428, как с четверкой. Когда умножили на двадцать три, вышло 3285711, но когда переднюю тройку прибавили к последней цифре, опять вышло 285714, как с двойкой. Умножили на восемьдесят девять, получилось 12741273. А когда 12 взяли спереди и прибавили обычным образом к тому, что осталось, вышло 741 285.
— Ну вот, — сказал Илюша, — теперь уже не то.
— Невелика разница! — мрачно ответил магистр. — Только дне цифры перескочили. А в остальном все то же самое.

Илюша начал внимательно осматривать умножения. Все было верно.
— В чем тут дело? Можешь ты выяснить, есть у этой нелепой штуки если не смысл, то по крайней мере хоть начало?
— По-видимому, — сказал неторопливо Илюша, — здесь получается тоже циклическая перестановка.
— Что?! — произнес словно насмерть перепуганный командор. — Что за чудные речи достигли моего скромного слуха?
Илюша посмотрел на него. Командор стоял подбоченясь, высоко задрав голову. Он мгновенно исцелился от своего отчаяния и обрел снова прекрасное настроение.
— Какая прелесть! — сказал он. — Вот какой замечательный юноша! И как остроумно — назвать это мое убогое, нескладное колесо… циклом! И моя бедная речь… О чем я там писал? Ах, вспомнил! О способах произношения цикловидных слов. Как раз!
Илюша беспомощно оглянулся на Радикса, но, кроме равнодушия, на его личике абсолютно ничего нельзя было прочесть.
А доктор продолжал:
— В жизнь мою не слыхал я ничего столь ученого. А скажите, великий победитель Бушмейстера, к чему вы изволили произнести эти таинственные слова? Даже в допущении, что вы правы, что из этого следует?
Но Илюша стоял красный как рак и молчал как рыба.
Увы, он не знал, что отвечать! Перестановка была, конечно, циклическая, это верно, но почему? Об этом-то Илюша не мог ничего сказать. И, в общем, получилось, что Уникурсал Уникурсалыч прав: произнести эти слова Илюша сумел, а объяснить, что хотел сказать, не мог. Мальчик решил не сдаваться. Поэтому стал снова рассматривать все свои умножения: на
— 151 —
два, на три, на четыре, на пять, на шесть… Так. А на семь? Нет, на семь он не множил. По-видимому, Кандидат Тупиковых Наук не заставлял его множить на семь. А ну-ка попробуем! Илюша умножил 142 857 на семь и получил 999 999.
«Вот странная история! — подумал он. — Все цифры давали один и тот же фокус, а если на семь помножить, получается совсем не то…»
Илюша снова начал внимательно осматривать результаты своих умножений и обратил внимание на то, что если написать число два раза подряд, то есть 142 857142 857, то при умножении на семь получится не шесть, а уже двенадцать девяток, и, следовательно, повторяя этот порядок цифр, можно получить умножением на семь любое число девяток… Что же это значит? Илюша обратил внимание на то, что получалось при умножении на два и на одиннадцать. Мальчик вдруг храбро схватил мел и написал:
В это время Радикс пробормотал себе под нос очень неразборчиво: «Слюнки капали с усов…» Тут Илюша воодушевился и начал делить единицу на семь. Как он и ожидал, получил в результате 0,142857142857… При этом он заметил, что остатки шли следующим образом: 3, затем 2, потом 6, вслед за этим 4 и, наконец, 5, что и объяснило всю загадку командорского колеса. И он написал рядом с делением еще столбик цифр:

— 152 —
Илюша обернулся и увидел, что Уникурсал Уникурсалыч смотрит так, будто потерял всякий интерес к проблеме колеса.
— Это одна седьмая, — сказал Илюша, — вот и все. Цикл в данном случае — это период дроби. А множители вы называли в том порядке, в котором идут остатки при делении, чтобы ваше колесо после каждого умножения поворачивалось как раз на одну цифру.
— Одна седьмая! Одна седьмая! — сердито повторил Уникурсал Уникурсалыч. — А что, если я возьму колесообразное число и разделю его пополам, по три цифры в каждой половинке. У меня будут теперь два числа — 142 и 857. Если я их сложу, то получу 999. Могу разбить и на три: 14, потом 28 и 57. Сложу и получаю снова 99. А это что означает?
Илюша внимательно посмотрел на свою табличку и ответил:
— Если я возьму 0,142, то это будет одна седьмая с точностью до одной тысячной, а если возьму 0,857, это будет шесть седьмых с той же точностью. Если их сложить, будет семь седьмых, то есть единица. Так как мои дроби не очень точные, то я получаю вместо единицы 0,999. То же и с тремя числами.
— А зачем ты множил 1 571427 на два?- спросил Радикс.
— Потому что мне показалось, что это похоже на половину архимедова числа. Я перемножил, получил 3,14 с лишним, и тут-то я убедился, что это одна седьмая[14].
— 153 —
— А кстати, скажи, умеешь ли ты сокращать дроби? Сократи шестнадцать шестьдесят четвертых.
Илюша пожал плечами, написал дробь, сократил ее на четыре, потом еще раз на четыре. Вышла одна четвертая.
— Какая невероятная канитель! — сказал с отвращением командор. — Выспаться можно, покуда ты тут возился. Вот, как я сокращаю.
Командор взял мел и написал:
16 / 64 =
… и вычеркнул шестерки…
= 1 / 4
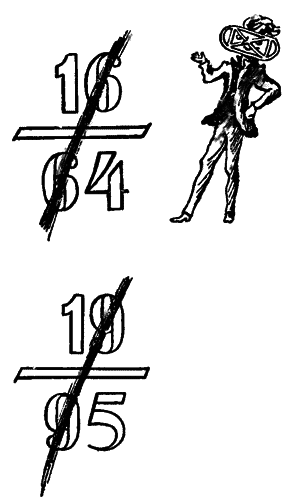
— Это случайно так у вас вышло, — ответил Илюша.
— Как это случайно? — возопил командор. — Пожалуйста!
И он написал следующее равенство:
19 / 95 =
… а теперь девятки …
= 1 / 5
14
В это время кто-то сказал Илюше на ухо: «Достань себе книжку Г. Радемахера и О. Теплица «Числа и фигуры» и почитай там рассказ двадцать третий о периодических десятичных дробях. Он занимает всего восемнадцать страниц. Если тебе покажется мало, бери «Теорию чисел» И. В. Арнольда. Только там побольше восемнадцати страниц!»
Тут Илюша заметил, что кто-то с ним раскланялся и сел на какую-то длинную палку верхом (а на палке написано: «Ось большая эллиптическая») и со свистом улетел в неизвестность…
Между прочим, в «Архимедовом лете» имеется рассказ о сравнениях (AЛ-I, XI) и указания на систему вычетов, то есть остатков при делении на некоторое число. В данном случае возникает вопрос о степенных вычетах, или остатках при делении последовательных степеней числа 10 на знаменатель данной дроби.