— По-моему, я такую параболу видел, — вспомнил Илюша, — в Схолии Шестнадцатой, там еще была и такая, которая у вас здесь под номером третьим.

— Это верно, — подтвердил Радикс, — так и было.

— В этом последнем случае, значит, — продолжал Илюша, — эти комплексные корни будут: один а + bi, а другой, ему сопряженный, а — bi.

— Конечно, — подтвердил Мнимий. — Но ведь это еще отнюдь не все. Самое удивительное качество решения кубического уравнения, которое крайне поразило алгебраистов шестнадцатого века, заключается в том, что иногда попадается такое кубическое уравнение, что если мы станем решать его по Кардановой формуле, то, невзирая на то что все три корня его вещественны, формула Кардана выражает эти корни мнимыми радикалам и, и можно доказать, что ничего иного из формулы Кардана вообще получить невозможно. То есть истинное решение словно прячется за мнимостями! Это тот случай, который Кардан называл «неприводимым» (Кардан уже знал, что у кубического уравнения три корня). Тут болонские алгебраисты впервые убедились, что наши мнимые человечки действительно существуют, активно участвуют в алгебраических построениях и при решении самой вещественной задачи невозможно обойтись без того, чтобы с ними не встретиться. Тут надо вот что еще иметь в виду: обычные чи-

— 436 —

сла человек придумал для счета. Всякого рода задачи, которые пришлось решать, привели неизбежно к понятию различных математических образов, которые получаются по крайней мере из пары чисел, как, например, сумма, разность, произведение, частное или дробь. А затем уже пошли еще более сложные построения, как и мы, мнимые человечки, которые выросли из задач, связанных с квадратным уравнением. Счет — одно, а расчет — другое! Но именно для того, чтобы наши расчеты не противоречили простому счету, чтобы правильность счета нигде и никогда не нарушалась, и приходится вводить такие сложные и хитрые построения, где из пары чисел получается одно особенное число. Но ведь зато и результаты получаются обширные и замечательные! Однако самая суть дела в том, что кубическое уравнение с его необычайными сложностями заставило математиков понять, что мы, мнимые хитроумные человечки (от которых до той поры, встречаясь с нами в квадратных уравнениях, просто отмахивались!), вовсе не случайные призраки, а самые настоящие граждане и деятели математического мира!

— Все-таки трудно… — признался Илюша.

— Разумеется, не очень просто, — согласился Мнимий. — Но вы подумайте еще о том, что в те времена все это было еще трудней, потому что нашей удобной алгебры с буквенными знаками еще не существовало. Тарталья, кстати сказать, изложил формулу Кардана в стихах, а потребовалось ему для этого двадцать пять строк!

— Ого, — отозвался Илюша, — целая поэма!

— Вот именно. И что было делать с этой формулой, как рассудить о ее странностях, долгое время не знали. Пока кубическое уравнение таково, что у него только один действительный корень, выражение под квадратным корнем

(q/2)² + (p/3)³

больше нуля, и тогда вычисления не так трудны. Но в другом случае — и как будто в самом простом, ибо тогда все три корня действительны! — это выражение становится меньше нуля, и как быть с формулой, неясно. Только через четверть века Рафаэль Бомбелли, последователь Кардана, нашел выход из положения. Начал он, как нередко в таких случаях бывает, с частного случая, с численного примера. Он взял такое кубическое уравнение:

x³ — 15x = 4

Решить его ничего не стоит без всякой формулы… Как вы скажете?

— 437 —

Илюша в ужасе уставился на уравнение. Наконец еле выдавил из себя:

— Четыре в квадрате — шестнадцать, а здесь пятнадцать, а четыре в кубе — шестьдесят четыре… Мне кажется, что решение равно четырем, потому что:

64 — 15 · 4 = 64 — 60 = 4.

— Вы совершенно правы! — весело воскликнул Мнимий. — Как видите, решить совсем нетрудно. А теперь попробуйте с формулой Кардана. И тотчас получается:

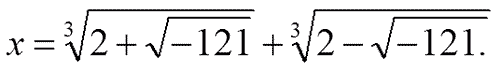
Как тут быть, неизвестно. Из (+ 121), конечно, квадратный корень извлечь небольшая хитрость, но ведь здесь минус.

Однако попробуем переписать теперь это по-нашему:

Из этого выражения Бомбелли получил (как мы теперь пишем!) такие равенства:

Если вы возведете каждое из этих равенств в куб, пользуясь формулой сокращенного умножения, вам хорошо известной, вы убедитесь, что равенства эти справедливы. Поскольку искомый икс равняется сумме этих двух выражений, то мы получаем…

Илюша немедленно написал ответ:

х = (2 + i) + (2 — i) = 2 + 2 = 4.

— Выходит, — решил он, — что искомый корень представился в виде суммы двух сопряженных комплексных чисел, а эта сумма, как мы уж знаем, есть действительное число! Значит, оно только спряталось за мнимыми числами. Но ведь должны быть и другие корни? Их ведь два еще должно быть как будто? Как их найти? Один корень мы нашли, — рассуждал Илюша, — левая часть уравнения должна состоять из трех

— 438 —

множителей. Но из нашего решения ясно, что один из множителей будет равен

(x — 4);

значит, если я перенесу все члены нашего уравнения влево и разделю затем эту левую часть на этот одночлен, получится квадратное уравнение, а из него можно раздобыть остальные два корня:

(x³ — 15x — 4) / (x — 4) = x³ + 4x + 1

Илюша еще немного покопался с вычислениями и написал:

x₁ = 4,000; x₂ = —2 + √3; x₃ = —2 — √3

или приближенно:

х₂ = —0,268; х₃ = —3,732.

— По теореме Виеты выходит. И сумма корней равна нулю! Попробую проверить значения корней. Для этого я буду придавать иксу целочисленные значения от минус шести до плюс шести и посмотрю, где кривая пересечет ось абсцисс.

Илюша так и сделал. Получилась табличка, а за ней и кривая, которую можно разглядеть на чертеже[38].

x	x3	- 15x	Свободый член	Сумма
- 6	- 216	+ 90	- 4	- 130
- 5	- 125	+ 75	- 4	- 54
- 4	- 64	+ 60	- 4	- 8
- 3	- 27	+ 45	- 4	+ 14
- 2	- 8	+ 30	- 4	+ 18
- 1	- 1	+ 15	- 4	+ 10
0	0	0	- 4	- 4
+ 1	+ 1	- 15	- 4	- 18
+ 2	+ 8	- 30	-4	- 26
+ 3	+ 27	- 45	- 4	- 22
+ 4	+ 64	- 60	- 4	0
+ 5	+ 125	- 75	- 4	+ 46
+ 6	+ 216	- 90	- 4	+122